【2021年蓝桥杯Java-B组省赛（第二场）题解】

一、求余（水）

$$在C/C++/Java/Python等语言中，使用\%表示求余，请问2021\%20的值是多少？$$

答案：1

二、双阶乘（水）

只要最后五位，取余就行。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        long ans = 1;
        for (int i = 3; i <= 2021; i++) {
            if (i % 2 == 1) {
                ans = ans * i % 100000;
            }
        }
        System.out.println(ans);
    }
}

答案：59375

三、格点（水）

第一象限的格点，就是x > 0 且 y > 0 且x、y都是整数，穷举。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        int ans = 0;
        for (int i = 1; i <= 2021; i++) {
            for (int j = 1; j <= 2021; j++) {
                if (i * j <= 2021) ans++;
                else break;
            }
        }
        System.out.println(ans);
    }
}

答案：15698

四、整数分解（剪枝优化、记忆化搜索）

相同数字不同位置算作不同分解方法，暴力要优化一下。对于一个大于2的正整数n，如果拆分成俩个正整数（不同位置算不同方案），可以拆出n - 1种方式。

所以，我们只需要遍历前3个数即可，后2个数可以直接判断。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        long ans = 0;
        for (int i = 1; i <= 2021; i++) {
            for (int j = 1; j <= 2021; j++) {
                if (i + j >= 2021) {
                    break;
                }
                for (int k = 1; k <= 2021; k++) {
                    // 剪枝优化
                    int tmp = 2021 - i - j - k;
                    // 只要tmp >= 2，剩下两个数就能够分
                    if (tmp >= 2) {
                        ans += tmp - 1;
                    } else {
                        break;
                    }
                }
            }
        }
        System.out.println(ans);
    }
}

下面再给出一种记忆化搜索的方法：因为对当前状态起作用的就只有两个变量，一个是当前剩余数，和剩余和，所以基于这两个变量就可以写一个Dp Table来记录搜索结果。

import java.util.*;

public class Main {
    static long[][] f = new long[6][2022];
	public static void main(String[] args) {
    	// 5个数凑出2021
		for (int i = 0; i < 6; i++) {
			Arrays.fill(f[i], -1);
		}
		System.out.println(dfs(5, 2021));
    }
    static long dfs(int n, int sum) {
    	if (f[n][sum] != -1) return f[n][sum];
    	if (n == 0) {
    		if (sum == 0) {
    			return 1;
    		}
    		return 0;
    	}
    	f[n][sum] = 0;
    	for (int i = 1; i <= sum; i++) {
    		f[n][sum] += dfs(n - 1, sum - i);
    	}
    	return f[n][sum];
    }
}

可以看出，记忆化搜索写出来的代码更加优雅，速度也更快，非常舒服！

答案：691677274345

五、城邦（最小生成树）

第一场考的最短路径，第二场考的最小生成树，有点意思哈哈哈哈哈。

import java.util.*;

public class main {
    public static void main(String args[]) {
        // 依次编号从1 - 2021
        List<int[]>edges = new LinkedList<>();
        // 存边
        for (int i = 1; i <= 2021; i++) {
            for (int j = i + 1; j <= 2021; j++) {
                edges.add(new int[]{i, j, getNum(i, j)});
            }
        }
        // 记得给边排序！
        Collections.sort(edges, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[2] - o2[2];
            }
        });
        // 并查集
        class UF {
            // 连通分量个数
            int count;
            // 保存每棵树
            int[] parent;
            // 保存每棵树的大小
            int[] size;
            // 构造函数
            UF(int n) {
                this.count = n;
                this.parent = new int[n];
                this.size = new int[n];
                // 初始化
                for (int i = 0; i < n; i++) {
                    parent[i] = i;
                    size[i] = 1;
                }
            }
            // 找x的根节点
            public int find(int x) {
                while (parent[x] != x) {
                    parent[x] = parent[parent[x]];
                    x = parent[x];
                }
                return x;
            }
            // 判断是否相连
            public boolean connected(int p, int q) {
                return find(p) == find(q);
            }
            // 连通两个节点
            public void union(int p, int q) {
                int rootP = find(p);
                int rootQ = find(q);
                // 已经相连
                if (rootP == rootQ) return;
                // 小树连在大树下
                if (size[rootP] > size[rootQ]) {
                    parent[rootQ] = rootP;
                    size[rootP] += size[rootQ];
                } else {
                    parent[rootP] = rootQ;
                    size[rootQ] += size[rootP];
                }
                // 连通分量--
                count--;
            }
            // 返回连通分量个数
            public int count() {
                return count;
            }
        }
        // 从1 - 2021
        UF uf = new UF(2022);
        int mst = 0;
        for (int[] node : edges) {
            if (uf.connected(node[0], node[1])) continue;
            uf.union(node[0], node[1]);
            mst += node[2];
        }
        // 注意节点0不会用到，所以剩余的连通分量应该 = 2
        if (uf.count() == 2) {
            System.out.println(mst);
        } else {
            System.out.println(-1);
        }
    }
    public static int getNum(int m, int n) {
        int sum = 0;
        while (m != 0 || n != 0) {
            if (m % 10 != n % 10) {
                sum += m % 10;
                sum += n % 10;
            }
            m /= 10;
            n /= 10;
        }
        return sum;
    }
}

答案：4046

一定要掌握最小生成树和最短路径问题的模板，这种题目只要会模板就是送分的。最小生成树需要建边，需要给边按照权值从小到大排序。最短路径需要建图，需要遍历当前节点相邻的节点。

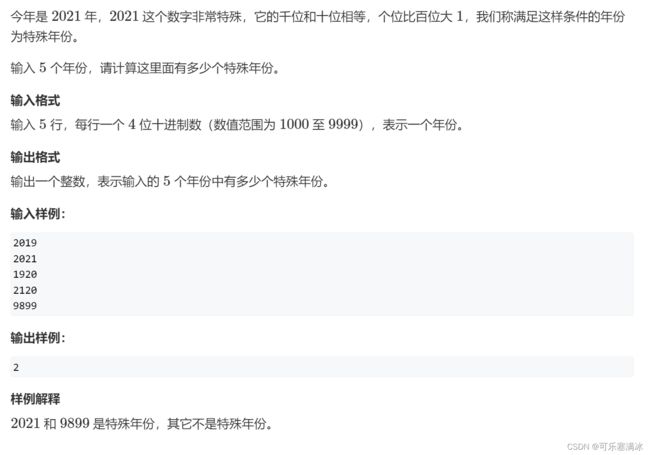
六、特殊年份（水）

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int ans = 0;
        for (int i = 0; i < 5; i++) {
            int year = scan.nextInt();
            String str = Integer.toString(year);
            if (str.charAt(0) == str.charAt(2) && str.charAt(3) - str.charAt(1) == 1) {
                ans++;
            }
        }
        System.out.println(ans);
    }
}

七、小平方（水）

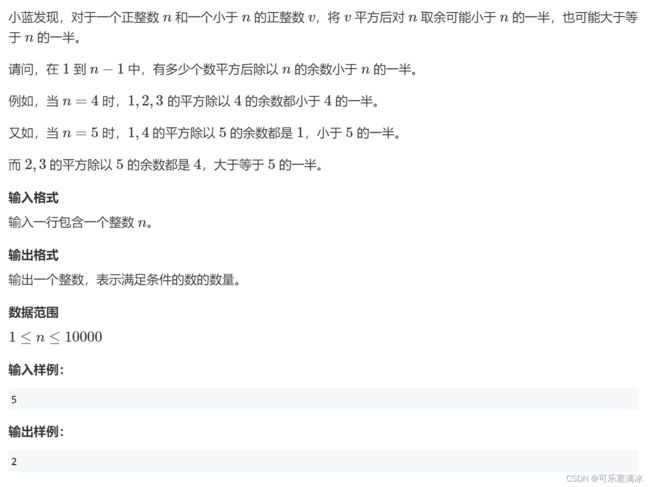
需要注意的是整数除法，5 / 2 = 2，但实际=2.5，所以得往3考虑，要进行四舍五入。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int ans = 0;
        for (int i = 1; i <= n - 1; i++) {
            double tmp = n * 1.0 / 2;
            int s = (int)(tmp + 0.5);
            if ((i * i) % n < s) {
                ans++;
            }
        }
        System.out.println(ans);
    }
}

八、完全平方数（数学定理）

又是这种大规模数据的数论题目，不能硬来。对于完全平方数而言，它的质因子的指数为偶数（不考虑1），质因子：1 2 3 5 7 11 13 17 19 23… 4 = 2 * 2，9 = 3 * 3，16 = 2 * 2 * 2 * 2，25 = 5 * 5，都是质因子的偶数幂。

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。质因子的意思就是素数因子。

把一个合数用质因数相乘的形式表示出来，叫做分解质因数。质因子是不含1的。

质因子分解代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        // 从最小素数开始
        int k = 2;
        while (k * k <= n) {
            if (n % k == 0) {
                System.out.printf("%d", k);
                n /= k;
                System.out.println();
            } else {
                k++;
            }
        }
    }
}

这里不需要对k是否为质数进行check，直接除，每次输出的一定是质数。

36 = 2 * 2 * 3 * 3，对于一个完全平方数，它的质因数的指数总是个偶数，遍历所有质因子，将指数为奇数的质因子累乘起来，再与n相乘，这样就保证了所有的质因子的指数为偶数，那就一定是完全平方数，且是最小的。

非质数，即合数，一定可以进行质因子分解，其中每个质因子的指数为偶数的，为完全平方数。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        long n = scan.nextLong();
        long res = 1;
        // 只需要考虑到根号n即可
        for (long i = 2; i * i <= n; i++) {
            if (n % i == 0) {
                int cnt = 0;
                while (n % i == 0) {
                	// n也是跟着除的
                    n /= i;
                    cnt++;
                }
                // 累乘指数为奇数的质因子
                if (cnt % 2 == 1) {
                    res *= i;
                }
            }
        }
        // n为质数时，res=1，满足
        System.out.println(res * n);
    }
}

上面的解法就是为了保证，当前数的所有质因子的指数为偶数，不是偶数就再乘个该质因子。

九、负载均衡（模拟 + 优先队列（堆））

说实话，题目越长，越简单（开玩笑~）

直接模拟，用优先队列，也就是所谓的堆去存储一个个节点，这个节点存储着当前任务的结束时刻，和恢复体力值，考虑到有多个计算机，应该要用优先队列数组进行存储。

再次强调Java中使用System.out.println速度过慢的问题，改用BufferedWriter，打印的时候将输出内容转换为String类型即可。

import java.io.*;
import java.util.*;

// 记录当前计算机中任务的结束时刻，和恢复体力值
class node{
    int reHour;
    int health;
    node(){};
    node(int reHour, int health) {
        this.reHour = reHour;
        this.health = health;
    }
}
public class Main {
    // 加快打印速度
    static BufferedWriter log = new BufferedWriter(new OutputStreamWriter(System.out));
    public static void main(String args[]) throws IOException {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int m = scan.nextInt();
        // 运算能力
        int[] com = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            com[i] = scan.nextInt();
        }
        // 构建优先队列
        Queue<node>[] pq = new PriorityQueue[n + 1];
        for (int i = 0; i < n + 1; i++) {
            pq[i] = new PriorityQueue<>(new Comparator<node>() {
                @Override
                // 按照恢复时间从小到大排序
                public int compare(node o1, node o2) {
                    return o1.reHour - o2.reHour;
                }
            });
        }
        int a, b, c, d;
        for (int i = 0; i < m; i++) {
            // 第 i 个任务在 ai 时刻分配，指定计算机编号为 bi，耗时为 ci 且算力消耗为 di
            // 如果此任务成功分配，将立刻开始运行，期间持续占用 bi 号计算机 di 的算力，持续 ci 秒
            a = scan.nextInt();
            b = scan.nextInt();
            c = scan.nextInt();
            d = scan.nextInt();
            // 注意任务执行完，算力是可以恢复的
            while (!pq[b].isEmpty()) {
                node tmp = pq[b].peek();
                if (tmp.reHour <= a) {
                    com[b] += tmp.health;
                    pq[b].poll();
                } else {
                    break;
                }
            }
            if (com[b] < d) {
                log.write(-1 + "");
                log.write("\n");
            } else {
                // 消耗计算机算力
                com[b] -= d;
                // 入队
                pq[b].offer(new node(a + c, d));
                log.write(com[b] + "");
                log.write('\n');
            }
        }
        log.flush();
    }
}

十、国际象棋（状压DP）

这种数据量下，不是数学规律就是DP，搜索时间不够。

本题作为DFS搜索练习题，也是极为不错的，有很多坑点。

import java.util.Scanner;

public class Main {
    static int MOD = 1000000007;
    static int ans = 0;
    static int n, m, k;
    // 方向数组
    static int[] xx = new int[] {1, 1, -1, -1, 2, 2, -2, -2};
    static int[] yy = new int[] {2, -2, 2, -2, 1, -1, 1, -1};
    static int[][] cnt;
    // 是否有马
//    static boolean[][] vis; 不能用vis数组来标记不能放马的位置，因为棋盘上某一点可能有多个马共同进行限制，需要对限制数计数
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        k = scan.nextInt();
        cnt = new int[n][m];
        // 从左上角第一个格子开始放，初始已放马的个数 = 0
        dfs(0, 0, 0);
        System.out.println(ans);
    }
    static void dfs (int x, int y, int horse) {
        if (horse == k) {
            ans = (ans + 1) % MOD;
            return;
        }
        // 切换到下一行第一个元素
        if (y >= m) {
            y = 0;
            x++;
            if (x >= n) return;
        }
        // 当前(x,y)位置不放马
        dfs(x, y + 1, horse);

        // 当前(x,y)位置放马
        // 先判断能否放马
        if (cnt[x][y] == 0) {
            cnt[x][y]++;
            // 遍历当前位置的马能够跳到的棋盘位置，标记为true
            for (int i = 0; i < 8; i++) {
                int tmpx = x + xx[i];
                int tmpy = y + yy[i];
                if (tmpx < 0 || tmpy < 0 || tmpx >= n || tmpy >= m) {
                    continue;
                }
                cnt[tmpx][tmpy]++;
            }
            // 放了马之后继续遍历
            dfs(x, y + 1, horse + 1);
            // 别忘了回溯
            // 回溯：一切在之前change过的变量，全都要恢复
            cnt[x][y]--;
            for (int i = 0; i < 8; i++) {
                int tmpx = x + xx[i];
                int tmpy = y + yy[i];
                if (tmpx < 0 || tmpy < 0 || tmpx >= n || tmpy >= m) {
                    continue;
                }
                cnt[tmpx][tmpy]--;
            }
        }
    }
}

回归正解：状压DP

状压DP还在修炼中…待更