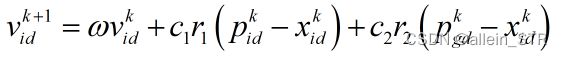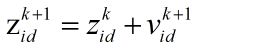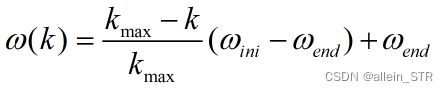【十问十答】粒子群算法（PSO）

目录

1. 粒子群算法基本思想是什么？

2. 标准PSO 算法流程是什么？

3. 采用粒子群优化权值和偏差值的方式训练模型有何优势？

4. 速度和位置更新公式中的参数含义

5. 参数分析与设置

6. PSO伪代码是什么

7. PSO优缺点是什么

8. PSO有什么应用

9. PSO实例1--优化神经网络权重Python

10. PSO实例2--求解函数最值Python

---

1. 粒子群算法基本思想是什么？

粒子群优化算法（Particle swarm optimization, PSO）的基本思想：是通过群体中个体之间的协作和信息共享来寻找最优解。

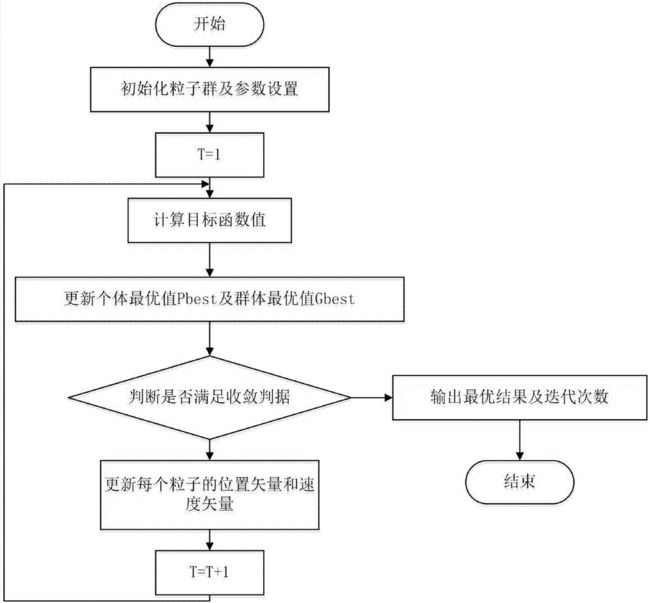
2. 标准PSO 算法流程是什么？

1）初始化一群微粒(群体规模为N)，包括随机位置和速度；
2）评价每个微粒的适应度；
3）对每个微粒，将其适应值与其经过的最好位置pbest作比较，如果较好，则将其作为当前的最好位置pbest；
4）对每个微粒，将其适应值与其经过的最好位置gbest作比较，如果较好，则将其作为当前的最好位置gbest；
5）根据公式(2)、(3)调整微粒速度和位置；
6）未达到结束条件则转第2）步。

迭代终止条件根据具体问题一般选为最大迭代次数Gk或(和)微粒群迄今为止搜索到的最优位置满足预定最小适应阈值

PSO算法过程的形象展示：

  

3. 采用粒子群优化权值和偏差值的方式训练模型有何优势？

1）. 采用粒子群优化方法获取最佳的权值和偏差值，可以提高模型的预测精度。

2）. 粒子群优化算法简单易行，可以提高模型的训练速度。

3.） 粒子群优化方法不容易陷入局部极值，原来的权重和偏差值更新方法容易陷入局部极值。

4. 速度和位置更新公式中的参数含义

速度更新公式为：

位置更新公式为：

其中，

• i=1,2,···,m。-----表示粒子个数
• d=1,2, ···,D. ------表示维数
• k------表示当前进化代数，或者说是当前迭代次数
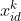• ------粒子当前的位置
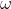• ------惯性因子, 为非负值。值较大时，全局寻优能力强，局部寻优能力弱；值较小时，全局寻优能力弱，局部寻优能力强。

计算公式为

------为惯性因子初始值，通常设置为0.4

------种群迭代到最大进化次数时的惯性因子值，通常设置为0.9

 ------最大迭代次数

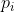• ------粒子当前最优位置
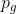• ------粒子i对应的全局最优位置
• r1和r2------随机初始为0-1之间的数，对群体的多样性有一定的作用
• c1和c2------学习因子（也称加速因子），影响算法的收敛速度

5. 参数分析与设置

• 群体规模N------一般取20～40，对较难或特定类别的问题可以取到100～200。
• 最大速度Vmax------决定当前位置与最好位置之间的区域的分辨率(或精度)。如果太快，则粒子有可能越过极小点；如果太慢，则粒子不能在局部极小点之外进行足够的探索，会陷入到局部极值区域内。这种限制可以达到防止计算溢出、决定问题空间搜索的粒度的目的。
• 惯性因子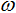------如果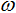＝0，则速度只取决于当前位置和历史最好位置，速度本身没有记忆性。
• 学习因子c1和c2------c1和c2代表将每个粒子推向pbest和gbest位置的统计加速项的权值。如果令c1＝c2＝0，粒子将一直以当前速度的飞行，直到边界，很难找到最优解。通常设c1＝c2＝2。Suganthan的实验表明：c1和c2为常数时可以得到较好的解，但不一定必须等于2。

6. PSO伪代码是什么

7. PSO优缺点是什么

优点：

• 不依赖于问题信息，算法通用性强。
• 需要调整的参数少，原理简单，容易实现
• 协同搜索，同时利用个体局部信息和群体全局信息指导搜索。
• 收敛速度快， 算法对计算机内存和CPU要求不高

缺点：

• 算法局部搜索能力较差，搜索精度不够高。
• 算法不能绝对保证搜索到全局最优解

8. PSO有什么应用

• 优化神经网络权重

• 函数优化

• 模式分类

• 模糊控制

9. PSO实例1--优化神经网络权重Python

#import tensorflow.compat.v1 as tf
#tf.compat.v1.disable_v2_behavior()
#import tensorflow as tf
#第一次用上面的语句跑的时候还好好的，再跑就报错了
import tensorflow as tf
tf = tf.compat.v1
tf.disable_v2_behavior()


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import random
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from sklearn.preprocessing import StandardScaler


def function(x1,y1,x2,y2,W):#  W是神经网络的W权重，根据这个权重设置神经网络


    #定义激活函数
    activation_function=tf.nn.relu
    #输入输出数据集
    xs=tf.placeholder(tf.float32,[None,None])
    ys=tf.placeholder(tf.float32,[None,None])


    #设计bp神经网络，三层，13,3,1
    weights_1=tf.Variable(W[0,:,:],tf.float32)
    biases_1=tf.Variable(tf.zeros([1,3])+0.1,tf.float32)
    wx_plus_b_1=tf.matmul( xs, tf.cast(weights_1,tf.float32))+biases_1
    outputs_1=activation_function(wx_plus_b_1)


    weights_2=tf.Variable(W[1,0:3,:],tf.float32)
    biases_2=tf.Variable(tf.zeros([1,3])+0.1,tf.float32)
    wx_plus_b_2=tf.matmul(outputs_1 , tf.cast(weights_2,tf.float32))+biases_2
    outputs_2=activation_function(wx_plus_b_2)


    w3=W[2,0:3,0].reshape(3,1)
    weights_3=tf.Variable(w3,tf.float32)
    biases_3=tf.Variable(0.1,tf.float32)

    wx_plus_b_3=tf.matmul(outputs_2,tf.cast(weights_3,tf.float32))+biases_3



    #预测输出结果
    prediction=wx_plus_b_3      #看来这里的数据就用行向量来输入输出

    #定义损失函数
    loss=tf.reduce_mean(tf.reduce_sum(tf.square(y1-prediction),reduction_indices=[1]))

    #梯度下降法训练
    train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)

    #初始化变量
    init=tf.global_variables_initializer()

    #执行会话，开始训练模型
    print("开始")
    with tf.Session() as sess:
        sess.run(init)
        for i in range (1000):
            sess.run(train_step,feed_dict={ xs:x1  , ys:y1 })

        end_loss=sess.run(loss,feed_dict={xs:x1,ys:y1})
        print(end_loss)
# print(sess.run(prediction,feed_dict={xs:x2}))
        print("结束")
    return end_loss


#导入数据集
data=load_boston()
data_pd=pd.DataFrame(data.data,columns=data.feature_names)
data_pd["price"]=data.target



#dataframe导入numpy
x=np.array(data_pd.loc[:,'CRIM':'LSTAT'])

y=np.array(data_pd.loc[:,'price'])

y.shape=(506,1)
#训练集测试集
x_train,x_test,y_train,y_test=train_test_split(x,y , test_size=0.1 )
#数据标准化
SC=StandardScaler()
x_train=SC.fit_transform(x_train)
y_train=SC.fit_transform(y_train)
x_test=SC.fit_transform(x_test)
y_test=SC.fit_transform(y_test)


#粒子数量num
num = 3

#粒子位置矩阵的形状
num_x = 3
num_y = 13
num_z = 3

#p为粒子位置矩阵，初始化为标准正态分布
p = np.random.randn(num,num_x,num_y,num_z)

#初始化粒子速度,以标准正态分布随机初始化
v = np.random.randn(num,num_x,num_y,num_z)

#个体最佳位置
good_p = np.array(p, copy=True)

#全局最佳位置
best_p = np.zeros((num_x, num_y, num_z))

#每次粒子移动后所计算出新的目标函数值
new_y = np.zeros(num)

#粒子个体历史最优值
good_y = np.zeros(num)

#粒子群体历史最优值
best_y = 0

#计算出初始粒子群的目标函数值
for i in range(num):
    good_y[i] = function(x_train, y_train, x_test, y_test, p[i, :, :, :])

#目标函数返回值是误差，那么最小的就是最优的
best_y = min(good_y)

#确定初始时最优位置
best_p = p[np.argmin(good_y), :, :, :]

#设置最大迭代次数
max_iter = 10

#开始迭代
for i in range(max_iter):

    #速度更新公式
    v = random.random() * v + 2.4 * random.random() * (best_p - p) + 1.7 * random.random() * ( good_p - p )

    #粒子位置更新
    p = p + v

    #计算每个粒子到达新位置后所得到的目标函数值
    for i in range(num):
        new_y[i] = function(x_train, y_train, x_test, y_test, p[i, :, :, :])

    #更新全局最优
    if min(new_y) < best_y:
        best_y = min(new_y)
        best_p = p[np.argmin(new_y), :, :, :]

    #更新个体历史最优
    for i in range(num):
        if new_y[i] < good_y[i]:
            good_y[i] = new_y[i]
            good_p[i, :, :, :] = p[i, :, :, :]  # 当对切片修改时，原始numpy数据也修改


print("结束")
print('目标函数最优值：',best_y)
print('此时的粒子位置：',best_p)

10. PSO实例2--求解函数最值Python

public class AlgorithmPSO {
	int n=2; //粒子个数，这里为了方便演示，我们只取两个，观察其运动方向
    double[] y;
    double[] x;
    double[] v;
    double c1=2;
    double c2=2;
    double pbest[];
    double gbest;
    double vmax=0.1; //速度最大值
    //适应度计算函数，每个粒子都有它的适应度
    public void fitnessFunction(){
        for(int i=0;igbest) gbest=y[i];
        }
        System.out.println("算法开始，起始最优解:"+gbest);
        System.out.print("\n");
    }
    public double getMAX(double a,double b){
        return a>b?a:b;
    }
    //粒子群算法
    public void PSO(int max){
        for(int i=0;ivmax) v[j]=vmax;//控制速度不超过最大值
                x[j]+=v[j];
                
                //越界判断，范围限定在[0, 2]
                if(x[j]>2) x[j]=2;
                if(x[j]<0) x[j]=0;
                
            }
            fitnessFunction();
            //更新个体极值和群体极值
            for(int j=0;jgbest) gbest=pbest[j];
                System.out.println("粒子n"+j+": x = "+x[j]+"  "+"v = "+v[j]);
            }
            System.out.println("第"+(i+1)+"次迭代，全局最优解 gbest = "+gbest);
            System.out.print("\n");
        }
        
    }
    //运行我们的算法
    public static void main(String[] args){
    	AlgorithmPSO ts=new AlgorithmPSO();
        ts.init();
        ts.PSO(10);//为了方便演示，我们暂时迭代10次。
    }

}

输出结果：

算法开始，起始最优解:0.0

粒子n0: x = 0.004  v = 0.004
粒子n1: x = 0.0  v = -4.065770842472382
第1次迭代，全局最优解 gbest = 0.007984

粒子n0: x = 0.01778510589090629  v = 0.013785105890906289
粒子n1: x = 0.0  v = -1.625639647649872
第2次迭代，全局最优解 gbest = 0.03525390179026183

粒子n0: x = 0.0610276658084214  v = 0.04324255991751511
粒子n1: x = 0.0  v = -0.6035255880722042
第3次迭代，全局最优解 gbest = 0.11833095562281844

粒子n0: x = 0.1610276658084214  v = 0.1
粒子n1: x = 0.0  v = -0.012719944703824898
第4次迭代，全局最优解 gbest = 0.29612542246113416

粒子n0: x = 0.2610276658084214  v = 0.1
粒子n1: x = 0.06231495466940402  v = 0.06231495466940402
第5次迭代，全局最优解 gbest = 0.4539198892994499

粒子n0: x = 0.3610276658084214  v = 0.1
粒子n1: x = 0.16231495466940402  v = 0.1
第6次迭代，全局最优解 gbest = 0.5917143561377656

粒子n0: x = 0.46102766580842136  v = 0.1
粒子n1: x = 0.262314954669404  v = 0.1
第7次迭代，全局最优解 gbest = 0.7095088229760813

粒子n0: x = 0.5610276658084213  v = 0.1
粒子n1: x = 0.362314954669404  v = 0.1
第8次迭代，全局最优解 gbest = 0.8073032898143969

粒子n0: x = 0.6610276658084213  v = 0.1
粒子n1: x = 0.462314954669404  v = 0.1
第9次迭代，全局最优解 gbest = 0.8850977566527127

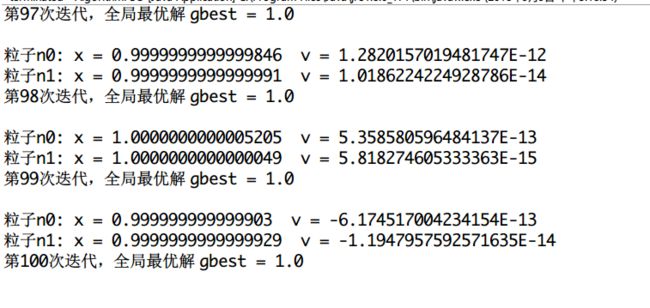
粒子n0: x = 0.7610276658084213  v = 0.1
粒子n1: x = 0.562314954669404  v = 0.1
第10次迭代，全局最优解 gbest = 0.9428922234910285

现在我们来观察两个粒子的位移x在每一次迭代中的变化（离食物的距离）。

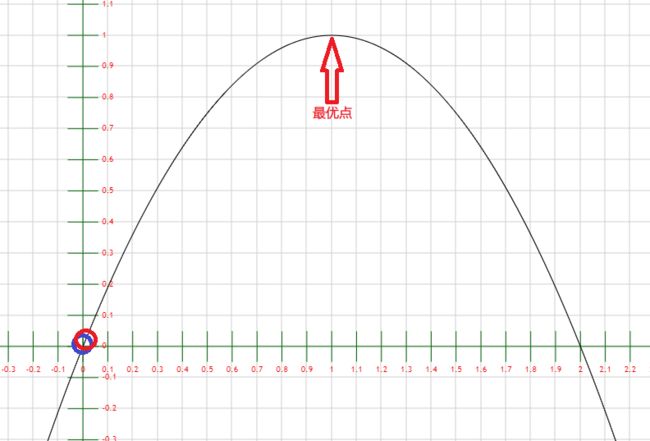
1) 初始状态

粒子n0: x = 0.0 v = 0.01

粒子n1: x = 2.0 v = 0.02

两个粒子位于区间两端。

2) 第一次迭代

粒子n0: x = 0.004 v = 0.004

粒子n1: x = 0.0 v = -4.065770842472382

两个粒子都跑到原点了。

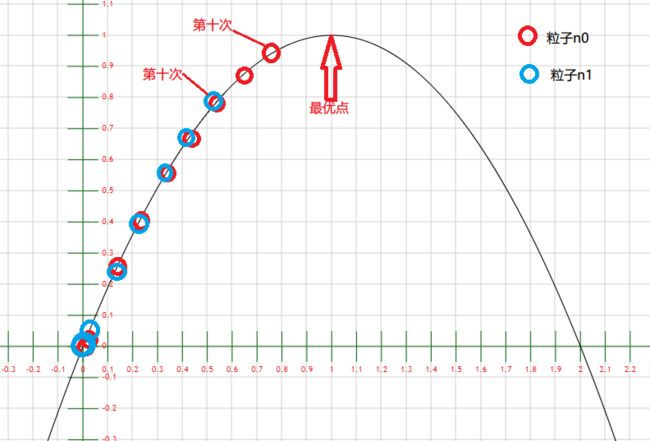
3) 第二、三……十次迭代

可以看到，两个粒子在不断靠近最优点。上面多个圈是他们聚集的过程，可以看出来，聚集过程是个越来越密集的过程。这才是10次迭代而已。如果我们加大迭代次数，很容易就找出最优解了。最后放上一个迭代100次的结果：

---

参考资料：

【算法】粒子群算法Particle Swarm Optimization超详细解析+代码实例讲解 - 云+社区 - 腾讯云 (tencent.com) 粒子群优化BP神经网络初始权值（python实现）_哈哈傻的博客-CSDN博客_粒子群优化bp神经网络

经典优化算法 | 粒子群算法解析 - 知乎 (zhihu.com)