链表题目：重排链表

题目

标题和出处

标题：重排链表

出处：143. 重排链表

难度

5 级

题目描述

要求

给定一个单链表的头结点。单链表可以表示为：

$${\text{L}}_{\text{0}}\to {\text{L}}_{\text{1}}\to \text{…}\to {\text{L}}_{\text{n - 1}}\to {\text{L}}_{\text{n}}$$

请将其重新排列后变为：

$${\text{L}}_{\text{0}}\to {\text{L}}_{\text{n}}\to {\text{L}}_{\text{1}}\to {\text{L}}_{\text{n - 1}}\to {\text{L}}_{\text{2}}\to {\text{L}}_{\text{n - 2}}\to \text{…}$$

不能修改结点的值，只能修改结点本身。

示例

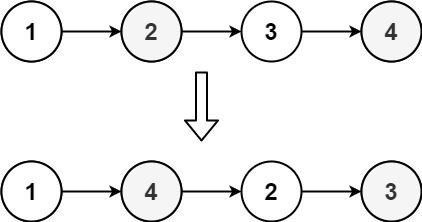
示例 1：

输入：$\text{head = [1,2,3,4]}$
输出：$\text{[1,4,2,3]}$

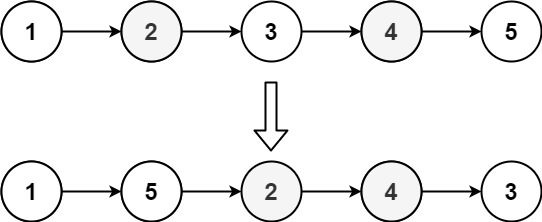
示例 2：

输入：$\text{head = [1,2,3,4,5]}$
输出：$\text{[1,5,2,4,3]}$

数据范围

• 链表中结点的数目范围是 $\text{[1, 5}\times {\text{10}}^{\text{4}}\text{]}$
• $\text{1}\le \text{Node.val}\le \text{1000}$

解法一

思路和算法

由于链表不支持随机访问，因此可以使用数组存储链表中的每个结点，然后通过数组随机访问链表中的每个结点。

遍历链表，将每个结点依次加入数组，则数组中的结点顺序和原始链表的结点顺序相同。根据重新排列的规则，需要将原始链表的结点按照从外到内的顺序连接，因此可以定义两个下标 $\text{left}$ 和 $\text{right}$ 分别指向首尾的待连接的结点，初始时 $\text{left}$ 和 $\text{right}$ 分别为头结点和尾结点的下标。

重新排列链表的操作如下：

1. 将 $\text{left}$ 指向的结点的后一个结点定为 $\text{right}$ 指向的结点，然后将 $\text{left}$ 的值加 $1$；

2. 如果 $\text{left}<\text{right}$，将 $\text{right}$ 指向的结点的后一个结点定为 $\text{left}$ 指向的结点，然后将 $\text{right}$ 的值减 $1$。

重复上述步骤直到 $\text{left}$ 和 $\text{right}$ 相遇，此时 $\text{left}$ 和 $\text{right}$ 都指向重新排列的链表的最后一个结点，需要将该节点的后一个结点定为 $\text{null}$，避免链表中出现环。

代码

class Solution {
    public void reorderList(ListNode head) {
        List<ListNode> nodes = new ArrayList<ListNode>();
        ListNode node = head;
        while (node != null) {
            nodes.add(node);
            node = node.next;
        }
        int left = 0, right = nodes.size() - 1;
        while (left < right) {
            nodes.get(left).next = nodes.get(right);
            left++;
            if (left < right) {
                nodes.get(right).next = nodes.get(left);
                right--;
            }
        }
        nodes.get(left).next = null;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是链表的长度。需要遍历链表中的每个结点一次，将结点加入数组，然后需要遍历数组中的每个结点一次，完成重新排列。

• 空间复杂度：$O(n)$，其中 $n$ 是链表的长度。需要创建长度为 $n$ 的数组存储链表中的每个结点。

解法二

思路和算法

解法一需要使用数组存储每个结点，空间复杂度是 $O(n)$。也可以不使用数组存储结点，将空间复杂度降低到 $O(1)$。

注意到如果将链表分成前一半和后一半，满足前一半和后一半的长度之差为 $0$ 或 $1$，则重新排列链表的结果等价于将前一半和反转后的后一半合并之后的结果。

首先找到链表的中间结点。可以使用「链表的中间结点」的快慢指针的做法，但是具体实现有所变化，当链表的结点数是偶数时，得到的是链表的第一个中间结点。快慢指针遍历结束时，快指针 $\text{fast}$ 移动到链表的尾结点或者倒数第二个结点，慢指针 $\text{slow}$ 移动到链表的中间结点。

链表的后一半为 $\text{slow}$ 后面的部分，不包含 $\text{slow}$。记 $\text{rightHead}:=\text{slow}.\text{next}$，则 $\text{rightHead}$ 为反转之前的后一半的头结点。得到 $\text{rightHead}$ 之后，令 $\text{slow}.\text{next}:=\text{null}$，将前一半和后一半的连接断开。

确定链表的前一半和后一半之后，将后一半反转，即反转从 $\text{rightHead}$ 到末尾的部分。反转链表的做法可以使用「反转链表」的迭代解法。

将后一半反转之后，将前一半和后一半合并。由于前一半和后一半的长度之差最多为 $1$，因此可以直接合并。

代码

class Solution {
    public void reorderList(ListNode head) {
        if (head == null) {
            return;
        }
        ListNode fast = head, slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        ListNode rightHead = slow.next;
        slow.next = null;
        ListNode prev = null, curr = rightHead;
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        ListNode node1 = head, node2 = prev;
        while (node1 != null && node2 != null) {
            ListNode temp1 = node1.next, temp2 = node2.next;
            node1.next = node2;
            node1 = temp1;
            node2.next = node1;
            node2 = temp2;
        }
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是链表的长度。需要使用快慢指针遍历链表，遍历链表的后一半并反转，以及反转后合并链表，每次遍历的时间复杂度都是 $O(n)$。

• 空间复杂度：$O(1)$。