深度学习入坑篇-全连接层及numpy实现

前言

卷积神经网络（ConvNets或CNNs）作为一类神经网络，托起cv的发展，本文主要介绍卷积神经网络的另外一个操作——全连接操作，其原理，并以小白视角，完成全连接从0到1的numpy实现。

1

做为小白入坑篇系列，开始今天的算子”FC“，错过其他算子的请关注公众号“所向披靡的张大刀”后台领取。

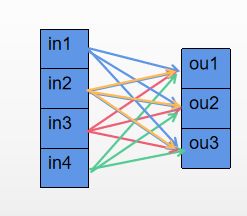
FC层是Full Connection的缩写，完全连接，意味着前一层的每个神经元都连接到下一层的每个神经元，简称全连接层，一般放在卷积神经网络中卷积、池化等操作后，原因之前的解释是，作为整个卷积神经网络要完成某项目标如“分类”任务时，会采用两步走战略：第一步对输入的数据提取特征，第二步将提取到的特征映射到分类目标上；这样卷积、池化以及激活函数等操作对应着第一步，做数据的特征工程，全连接层对应着第二步，对特征做特征加权，起到“分类器”的作用。

2

FC层其本质是传统的多层感知机（MLP），如下图所示：

如中间橙色的神经元值计算：

其中w为权重，bias为偏置，f为激活函数，每一个输出的神经元等于前一层中每个神经元的权重和+bias 后再激活。具体的多层感知机的前向和反向传递参考【1】。

而全连接层的激活函数一般使用softmax概率激活函数，使整个输出层的概念之和为1，softmax函数将任意分数的向量压缩成介于0到1之间，总和为1的值，softmax的激活函数的具体解释参见前一篇《激活函数及numpy实现》，

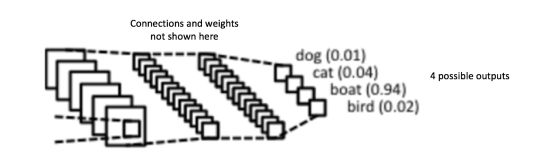
从提取特征到全连接层的操作，一般是将feature map直接展平后，通过全连接层到对应的分支上，如下图：

在输入“7”这张图片后，经过几轮卷积池化等的特征提取后，将feature map 展平成一根长条后，完成全连接操作（这里的图有误导，它没有feature map 展平的操作，但是上层每个神经元与下层feature map的每个值均有权重的连接，本质上是通过全局卷积来替代全连接操作），可以看下面细节图：

在实际使用中，全连接层可以由卷积操作实现，如果前层是卷积，后面是全连接层的网络可以转换成卷积核为h*w的全局卷积，如上图的张细节图所示的一样，例如一个h=3，w=3,channle=3的feature map，如果想输出的FC长度为2，那么则需要两个和feature map一样大的卷积，具体的卷积操作可以参见《卷积算子及numpy实现》，具体的实现大家可以自行推导下，其数学表达是一模一样的。这里推荐上图3D可视化的feature map视图【2】。

而如果前一层是全连接层的，可以通过1×1的卷积实现如下图所示：

一个长度为4的feature map全连接后变成长度为3，其本质与下图是一致的，长度为4的feature map可以看出 h和w均为1，channel为4的feature map, 可以通过输出长度个11输入长度的卷积核，卷积成输出长度的feature map,其数学表达是一样的:

实际上还有一种操作叫全局平均池化（GAP）操作, 以长宽等于feature map的长宽作为池化的size, 这样每一层仅有一个值，整个feature map的一个矩阵Tensor 经过全局池化后则变成一根vector，也完成了全连接的操作，可以说是替代全连接操作的另外一种方式，

据说因为FC层的数据冗余，所以GAP可以一定程度上防止过拟合，但是之前在某篇论文里看到说全局池化相比较FC收敛速度变慢，原因可能是在整个卷积网络中，如果采用FC层，FC层因为参数量大，数据冗余，所以两步走中的分类部分的学习均可以在FC层完成，对前面特征提取部分的压力比较小，但如选择GAP，全局池化比较简单粗暴，会对特征间的相互位置关系的表达不明显，而为了整个网络的有效表达，前面特征提取的卷积层等则要表达的更确切一点，而更确切的另外一层含义是泛化性会弱一些，这样会导致另外一个问题是在迁移学习的时候，特征提取部分要调整参数幅度比全连接层对应的卷积网络的幅度大，这里也说明了含有FC层的卷积神经网络在迁移训练上的泛化能力比较强。这里欢迎小伙伴讨论。

3

FC层的实现torch、tensorflow等框架中均已封装好，拿来即用，非常方便，这边是方便自己理解，通过numpy 从0实现全链接。思路如下，同样考虑继承Layers类，Layer类的代码参见conv算子中Layer类的实现。
FC层继承Layer类，前向和反向实现如下：

import numpy as np
from module import Layers

class FC(Layers):
    """
    前向：

    反向：反向先计算出来的值，需要和之前的输入值相乘，乘完后，再与lr相乘才是梯度
    """

    def __init__(self, name, in_channels, out_channels):
        super(FC).__init__(name)
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.weights = np.random.standard_normal((in_channels, out_channels))
        self.bias = np.zeros(out_channels)
        self.grad_w = np.zeros((in_channels, out_channels))
        self.grad_b = np.zeros((out_channels))

    def forward(self, input):
        self.in_shape = input.shape
        input = np.reshape(input,(input.shape[0], -1))
        self.input = input
        return np.dot(self.input, self.weights) + self.bias 

    def backward(self, grad_out):
        N =grad_out.shape[0]
        dx = np.dot(grad_out,self.weights.T)
        self.grad_w = np.dot(self.input.T, grad_out)
        self.grad_b = np.sum(grad_out, axis=0)
        return dx.reshape(self.input) 

    def zerp_grad(self):
        self.grad_w.fill(0)
        self.grad_b.fill(0)

    def update(self, lr):
        self.weights -=lr*self.grad_w
        self.bias -= lr*self.grad_b

FC层因为数据量大、冗余等原因，一直不太不被人重视，从上面的卷积和全连接可以相互替代，可以看出来，如果卷积是全局卷积，和FC层是一样的，全局卷积可以学习全局信息，全局之间的相互位置信息等，对一般卷积学习局部信息，通过增大感受野来扩大局部学习范围，但是一般卷积的数据量小啊，感觉一般卷积是计算量的一种妥协，现在的transformer等在cv上的应用，通过attention机制来学习整个feature map区域，就有点像全连接层的操作。这是后话，欢迎小伙伴一起讨论。

参考：
[1] https://ujjwalkarn.me/2016/08/09/quick-intro-neural-networks/
[2] https://www.cs.ryerson.ca/~aharley/vis/conv/
[3] https://www.zhihu.com/question/41037974/answer/150522307

更多深度学习请关注公众号“所向披靡的张大刀”