机器学习实践—基于Scikit-Learn、Keras和TensorFlow2第二版—第2章 端到端机器学习项目实践
本章使用California房价数据集进行案例分析
1. 导入所需的库
import os
import tarfile
import urllib
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
for i in [pd,np]:
print(i.__name__,": ",i.__version__,sep="")输出:
pandas: 0.25.3
numpy: 1.17.42. 下载数据集并进行拆分
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handsonml2/master/"
HOUSING_PATH = os.path.join("datasets","housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
os.makedirs(housing_path, exist_ok=True)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
fetch_housing_data()def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path,"housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head()输出:
housing.info()输出:
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
longitude 20640 non-null float64
latitude 20640 non-null float64
housing_median_age 20640 non-null float64
total_rooms 20640 non-null float64
total_bedrooms 20433 non-null float64
population 20640 non-null float64
households 20640 non-null float64
median_income 20640 non-null float64
median_house_value 20640 non-null float64
ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB housing["ocean_proximity"].value_counts()输出:
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
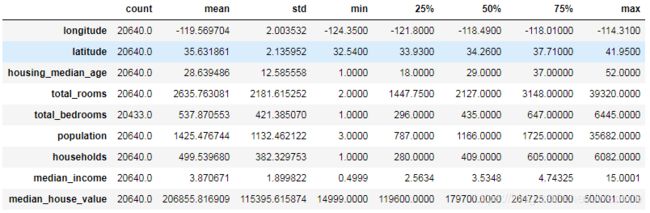
Name: ocean_proximity, dtype: int64housing.describe().T输出:
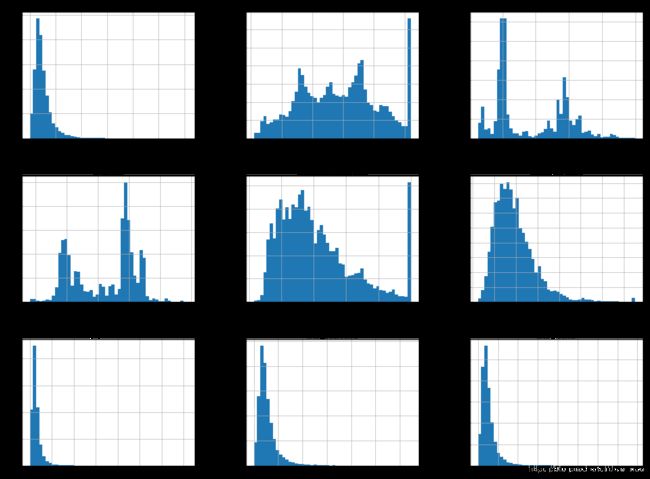
housing.hist(bins=50, figsize=(20,15))
plt.show()输出:
np.random.seed(42)
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data)*test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
print(train_set.shape, test_set.shape)输出:
(16512, 10) (4128, 10)from zlib import crc32
def test_set_check(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio*2**32
def split_train_test_by_id(data, test_ratio, id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio))
return data.loc[~in_test_set], data.loc[in_test_set]由于该数据集没有标识符列,最简单的做法是用行号当作ID:
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
train_set.head()输出:
如果用行号作为唯一标识符,则需要保证每次加入新数据时必须放在数据集的最后,同时需要保证数据集不能删除样本。如果无法保证以上两点,那么就需要重新用比较稳定的特征用标识符。例如,可以用联合经度和纬度作为标识符,因为经度和纬度是固定甚至永久不变的。
housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "id")
print(train_set.head())输出:
longitude latitude housing_median_age total_rooms total_bedrooms \
14196 -117.03 32.71 33.0 3126.0 627.0
8267 -118.16 33.77 49.0 3382.0 787.0
17445 -120.48 34.66 4.0 1897.0 331.0
14265 -117.11 32.69 36.0 1421.0 367.0
2271 -119.80 36.78 43.0 2382.0 431.0
population households median_income median_house_value \
14196 2300.0 623.0 3.2596 103000.0
8267 1314.0 756.0 3.8125 382100.0
17445 915.0 336.0 4.1563 172600.0
14265 1418.0 355.0 1.9425 93400.0
2271 874.0 380.0 3.5542 96500.0
ocean_proximity income_cat
14196 NEAR OCEAN 3
8267 NEAR OCEAN 3
17445 NEAR OCEAN 3
14265 NEAR OCEAN 2
2271 INLAND 3 sklearn中提供了多种函数用于切分数据。
- train_set_split():与split_train_set()函数功能几乎一致,另外增加了几个功能:一是增加了随机状态参数,设置随机种子。二是可以传入多个具有相同行标识符数据集,输出相同索引的切分数据,这在数据本身就分散状态时非常有用。
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
print(test_set.head())输出:
longitude latitude housing_median_age total_rooms total_bedrooms \
20046 -119.01 36.06 25.0 1505.0 NaN
3024 -119.46 35.14 30.0 2943.0 NaN
15663 -122.44 37.80 52.0 3830.0 NaN
20484 -118.72 34.28 17.0 3051.0 NaN
9814 -121.93 36.62 34.0 2351.0 NaN
population households median_income median_house_value \
20046 1392.0 359.0 1.6812 47700.0
3024 1565.0 584.0 2.5313 45800.0
15663 1310.0 963.0 3.4801 500001.0
20484 1705.0 495.0 5.7376 218600.0
9814 1063.0 428.0 3.7250 278000.0
ocean_proximity income_cat
20046 INLAND 2
3024 INLAND 2
15663 NEAR BAY 3
20484 <1H OCEAN 4
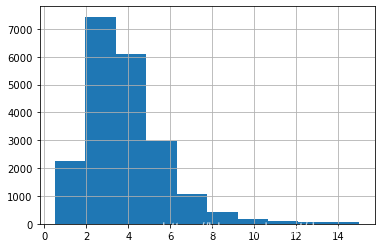
9814 NEAR OCEAN 3 housing["median_income"].hist()输出:
housing["income_cat"] = pd.cut(housing["median_income"],
bins=[0.,1.5,3.0,4.5,6.0,np.inf],
labels=[1,2,3,4,5])
housing["income_cat"].hist()输出:
现在可以根据收入进行分层抽样了:
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
print(strat_train_set.head())输出:
longitude latitude housing_median_age total_rooms total_bedrooms \
17606 -121.89 37.29 38.0 1568.0 351.0
18632 -121.93 37.05 14.0 679.0 108.0
14650 -117.20 32.77 31.0 1952.0 471.0
3230 -119.61 36.31 25.0 1847.0 371.0
3555 -118.59 34.23 17.0 6592.0 1525.0
population households median_income median_house_value \
17606 710.0 339.0 2.7042 286600.0
18632 306.0 113.0 6.4214 340600.0
14650 936.0 462.0 2.8621 196900.0
3230 1460.0 353.0 1.8839 46300.0
3555 4459.0 1463.0 3.0347 254500.0
ocean_proximity
17606 <1H OCEAN
18632 <1H OCEAN
14650 NEAR OCEAN
3230 INLAND
3555 <1H OCEAN strat_test_set["income_cat"].value_counts()/len(strat_test_set)输出:
3 0.350533
2 0.318798
4 0.176357
5 0.114583
1 0.039729
Name: income_cat, dtype: float64housing["income_cat"].value_counts()/len(housing)输出:
3 0.350581
2 0.318847
4 0.176308
5 0.114438
1 0.039826
Name: income_cat, dtype: float64def income_cat_proportions(data):
return data["income_cat"].value_counts()/len(data)
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
compare_props = pd.DataFrame({"Overall":income_cat_proportions(housing),
"Stratified":income_cat_proportions(strat_test_set),
"Random":income_cat_proportions(test_set)}).sort_index()
compare_props["Rand. %error"] = 100*compare_props["Random"]/compare_props["Overall"]-100
compare_props["Strat. %error"] = 100*compare_props["Stratified"]/compare_props["Overall"]-100
compare_props输出:
Overall Stratified Random Rand. %error Strat. %error
1 0.039826 0.039729 0.040213 0.973236 -0.243309
2 0.318847 0.318798 0.324370 1.732260 -0.015195
3 0.350581 0.350533 0.358527 2.266446 -0.013820
4 0.176308 0.176357 0.167393 -5.056334 0.027480
5 0.114438 0.114583 0.109496 -4.318374 0.127011可以看出分层抽样的结果收入分类比例与数据集全局比例基本一致,好于完全随机的抽样。因此说数据集拆分是机器学习项目中非常重要的步骤。
此时,可以将income_cat列删除掉。
for set_ in (strat_train_set, strat_test_set):
set_.drop("income_cat", axis=1, inplace=True)
print(strat_train_set.head())输出:
longitude latitude housing_median_age total_rooms total_bedrooms \
17606 -121.89 37.29 38.0 1568.0 351.0
18632 -121.93 37.05 14.0 679.0 108.0
14650 -117.20 32.77 31.0 1952.0 471.0
3230 -119.61 36.31 25.0 1847.0 371.0
3555 -118.59 34.23 17.0 6592.0 1525.0
population households median_income median_house_value \
17606 710.0 339.0 2.7042 286600.0
18632 306.0 113.0 6.4214 340600.0
14650 936.0 462.0 2.8621 196900.0
3230 1460.0 353.0 1.8839 46300.0
3555 4459.0 1463.0 3.0347 254500.0
ocean_proximity
17606 <1H OCEAN
18632 <1H OCEAN
14650 NEAR OCEAN
3230 INLAND
3555 <1H OCEAN strat_train_set.shape输出:
(16512, 10)3. 数据可视化和探索
此时,把测试集先放一边,专门研究训练集。复制一份训练集,以免在操作过程中修改掉原始训练集。
housing = strat_train_set.copy()3.1 可视化地理信息数据
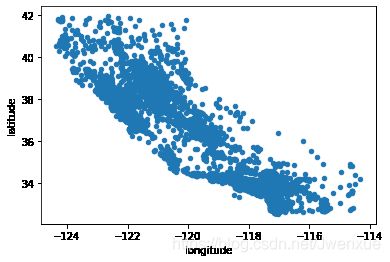
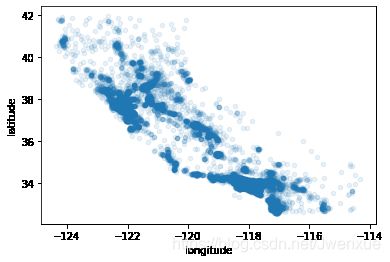
housing.plot(kind="scatter",x="longitude",y="latitude")输出:
根据经度和纬度绘制散点图,其形状很像加利福尼亚地形。但除此之外,很难一眼看出其它含义。
通过设置alpha参数,观察数据分布的密度。
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.1)输出:
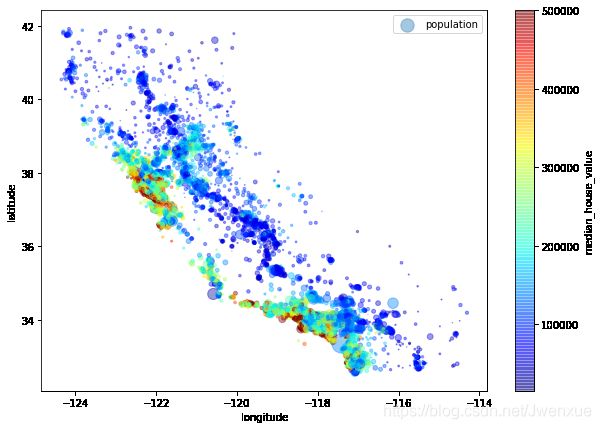
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
plt.legend()输出:
# 下载California地形图片
image_path = os.path.join("./images/end_to_end_project")
os.makedirs(image_path, exist_ok=True)
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
filename = "california.png"
print("Downloading",filename)
url = DOWNLOAD_ROOT + "images/end_to_end_project/"+filename
urllib.request.urlretrieve(url, os.path.join(image_path,filename))import matplotlib.image as mpimg
california_img = mpimg.imread(os.path.join(image_path, filename))
ax = housing.plot(kind="scatter", x="longitude", y="latitude",figsize=(10,7),
s=housing["population"]/100,label="Population",
c="median_house_value",cmap=plt.get_cmap("jet"),
colorbar=False, alpha=0.4)
plt.imshow(california_img, extent=[-124.55,-113.80,32.45,42.05], alpha=0.5,
cmap=plt.get_cmap("jet"))
plt.ylabel("Latitude",fontsize=14)
plt.xlabel("Longitude",fontsize=14)
prices = housing["median_house_value"]
tick_values = np.linspace(prices.min(),prices.max(),11)
cbar = plt.colorbar()
cbar.ax.set_yticklabels(["$%dk"%(round(v/1000)) for v in tick_values],fontsize=14)
cbar.set_label("Median House Value",fontsize=16)
plt.legend(fontsize=16)
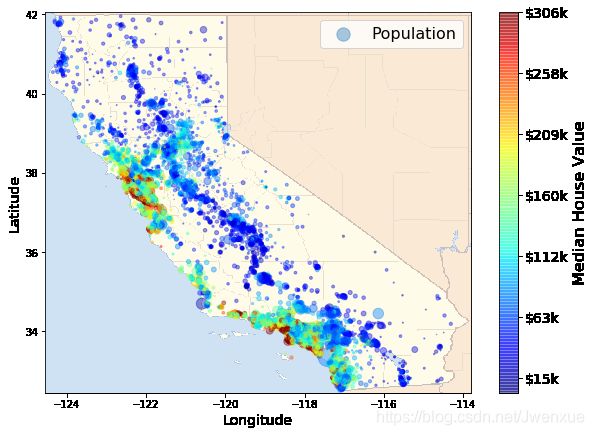
plt.show()输出:
对比地形图可以发现,大部分数据分布在湾区以及洛杉矶和圣地亚哥周围,再加上中央山谷的一长串密度相当高的地区,尤其是萨克拉曼多和弗雷斯诺附近。
这也从侧面反映出房价与地理位置和人口密度密切相关。
3.2 探索相关性
由于训练集不是很大,因此可以计算属性之间的标准相关系数,即皮尔森相关系数。
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)输出:
median_house_value 1.000000
median_income 0.687160
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population -0.026920
longitude -0.047432
latitude -0.142724
Name: median_house_value, dtype: float64相关系数取值-1到1。1表示正相关,-1表示负相关,0表示没有相关性。这种相关系数关系只针对线性相关性,不适应于非线性相关性。
Pandas scatter_matrix()函数可以可视化相关系数关系。由于特征太多,绘制的结果图很大,这里选择几个感兴趣的特征进行分析:
attributes = ["median_house_value","median_income","total_rooms","housing_median_age"]
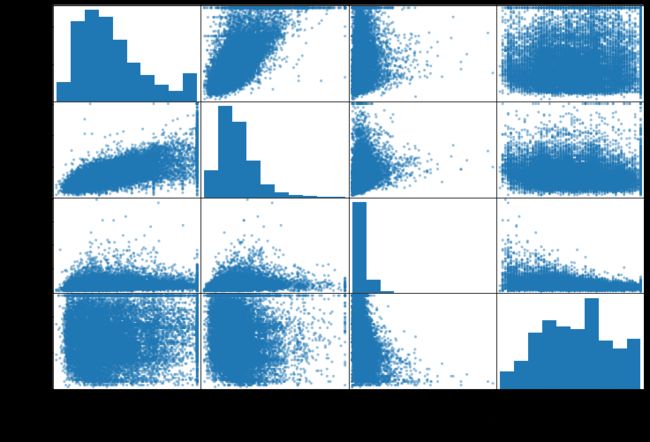
pd.plotting.scatter_matrix(housing[attributes],figsize=(12,8))输出:
从上述图中可以看出,median_house_value和median_income之间有较强的相关性。
将两个属性单独做图进行分析:
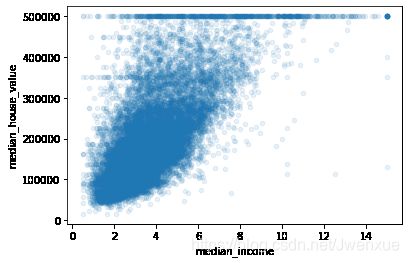
housing.plot(kind="scatter",x="median_income",y="median_house_value",alpha=0.1)输出:
上图表示:两个属性相关性很强,其次在50万附近有一条直线。
3.3 属性组合
如果抛开家庭总数,只关注房间总数就显得没有意义。而是应该关注每个地区平均每个家庭拥有的房间数。卧室数量也是同样的道理。
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"] # 平均每个家庭房屋数
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"] # 平均每个房屋卧室数
housing["population_per_household"] = housing["population"]/housing["households"] # 平均每个家庭人口数
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)输出:
median_house_value 1.000000
median_income 0.687160
rooms_per_household 0.146285
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population_per_household -0.021985
population -0.026920
longitude -0.047432
latitude -0.142724
bedrooms_per_room -0.259984
Name: median_house_value, dtype: float64惊奇地发现,房屋价格除了与收入很相关外,第二相关的就是刚刚新生成的属性平均每个家庭房间数。
同时可以发现,房屋价格与房屋平均卧室数具有最强负相关性,这也容易理解:卧室所占房屋比例越小,价格就越贵。
4. 模型准备数据
先将训练集训练特征与标签拆分开:
housing = strat_train_set.drop("median_house_value",axis=1)
housing_labels = strat_train_set["median_house_value"].copy()4.1 数据清洗
对于数据中的缺失值,有如下三种处理方法:
- 删除缺失值的样本
- 删除有缺失值的整个属性
- 用其它值填充缺失值(例如用0、平均值、中值等)
sample_incomplete_rows = housing[housing.isnull().any(axis=1)] # 取出所有空值的样本
print(len(sample_incomplete_rows))
sample_incomplete_rows.head()输出:
158
longitude latitude housing_median_age total_rooms total_bedrooms \
4629 -118.30 34.07 18.0 3759.0 433.0
6068 -117.86 34.01 16.0 4632.0 433.0
17923 -121.97 37.35 30.0 1955.0 433.0
13656 -117.30 34.05 6.0 2155.0 433.0
19252 -122.79 38.48 7.0 6837.0 433.0
population households median_income ocean_proximity
4629 3296.0 1462.0 2.2708 <1H OCEAN
6068 3038.0 727.0 5.1762 <1H OCEAN
17923 999.0 386.0 4.6328 <1H OCEAN
13656 1039.0 391.0 1.6675 INLAND
19252 3468.0 1405.0 3.1662 <1H OCEAN
说明在该数据集中总共有158条有缺失值的样本。分别用上面提到的三种方法进行处理:
方法一:
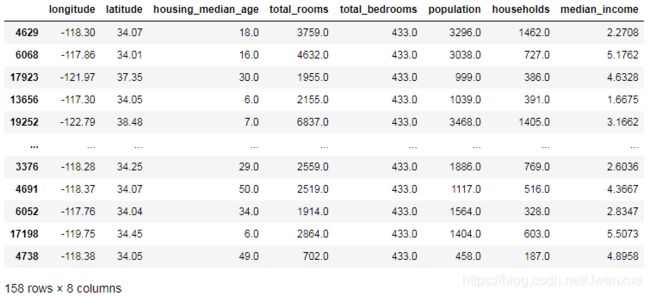
sample_incomplete_rows.dropna(subset=["total_bedrooms"])输出:
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income ocean_proximity方法二:
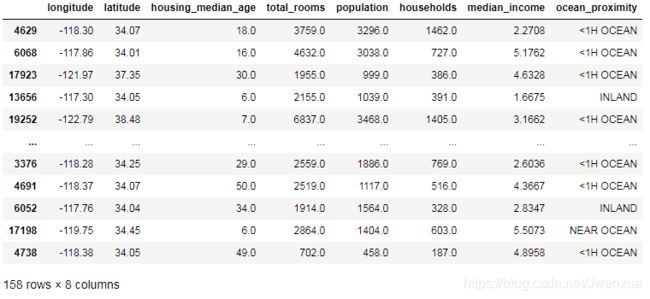
sample_incomplete_rows.drop("total_bedrooms",axis=1)输出:
方法三:
median = housing["total_bedrooms"].median()
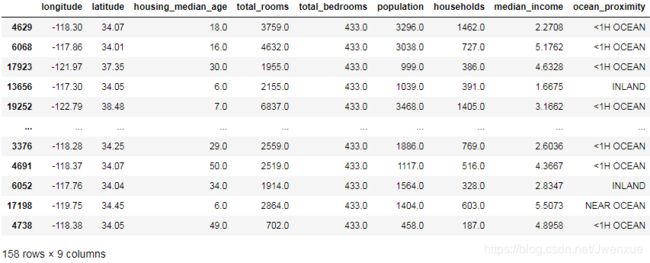
sample_incomplete_rows["total_bedrooms"].fillna(median, inplace=True)
sample_incomplete_rows输出:
注意:使用第三种方法时记得保存计算出的值。因为在测试集中也需要同样的操作。
skleanr提供了SimpleImputer类以方便处理这些缺失值:
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
housing_num = housing.drop("ocean_proximity",axis=1) # 由于中值只能对数字计算,所以删除字符串的列
imputer.fit(housing_num)输出:
SimpleImputer(add_indicator=False, copy=True, fill_value=None,
missing_values=nan, strategy='median', verbose=0)imputer.statistics_输出:
array([-118.51 , 34.26 , 29. , 2119.5 , 433. , 1164. ,
408. , 3.5409])housing_num.median().values输出:
array([-118.51 , 34.26 , 29. , 2119.5 , 433. , 1164. ,
408. , 3.5409])可以看到,imputer简单地计算了中值,并将其存储在statistics_中。
我们已经知道total_bedrooms中存在缺失值,但为了保险起见,对所有属性做中值填充。
X = imputer.transform(housing_num)
type(X)输出:
numpy.ndarray结果是NumPy arrary格式,可以将其再转换为Pandas DataFrame格式:
housing_tr = pd.DataFrame(X, columns=housing_num.columns,index=housing_num.index)
housing_tr.loc[sample_incomplete_rows.index.values]输出:
可以看到total_bedrooms中所有缺失值被填充成中值433
imputer.strategy输出:
'median'4.2 处理文本和类别属性
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)输出:
ocean_proximity
17606 <1H OCEAN
18632 <1H OCEAN
14650 NEAR OCEAN
3230 INLAND
3555 <1H OCEAN
19480 INLAND
8879 <1H OCEAN
13685 INLAND
4937 <1H OCEAN
4861 <1H OCEAN可以看到这些不是随机的文本,这些属于类别属性。sklearn中可以使用OridinalEncoder类将其转换成数字格式:
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded[:10]输出:
array([[0.],
[0.],
[4.],
[1.],
[0.],
[1.],
[0.],
[1.],
[0.],
[0.]])ordinal_encoder.categories_输出:
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]可以使用如上变量输出所有类别值。
对于类别属性,各个类别之间没有大小之分,因此用0,1,2,3,4做属性值时机器学习模型会认为数字越大特征越重要,这样是不符合实际需求的。对于这种情况,one-hot编码是更好的方式,sklearn中提供了OneHotEncoder类:
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot输出:
<16512x5 sparse matrix of type ''
with 16512 stored elements in Compressed Sparse Row format> 返回结果不是NumPy array格式,而是SciPy的稀疏矩阵。如果类别相当多时将会产生大量的新属性(列),并且结果中大部分位置都是0,只有很少位置是1,这就需要大量的存储空间。而稀疏矩阵的优点是只存储非0值的位置,节约空间。如果想转换成NumPy array格式,只需调用toarray()函数即可。
housing_cat_1hot.toarray()输出:
array([[1., 0., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1.],
...,
[0., 1., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 0., 0., 1., 0.]])cat_encoder.categories_输出:
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]或者可以指定sparse=False参数,结果将返回NumPy array格式:
cat_encoder = OneHotEncoder(sparse=False)
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot输出:
array([[1., 0., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 0., 0., 0., 1.],
...,
[0., 1., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 0., 0., 1., 0.]])4.3 自定义数据清洗类
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooom_ix, population_ix, households_ix = 3,4,5,6 # 列编号
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room = True):
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self # 不进行任何处理
def transform(self,X):
rooms_per_household = X[:,rooms_ix]/X[:,households_ix]
population_per_household = X[:,population_ix]/X[:,households_ix]
if self.add_bedrooms_per_room:
bedrooom_per_room = X[:,bedrooom_ix]/X[:,rooms_ix]
return np.c_[X,rooms_per_household,population_per_household,bedrooom_per_room]
else:
return np.c_[X,rooms_per_household,population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)housing_extra_attribs = pd.DataFrame(housing_extra_attribs,
columns=list(housing.columns)+["rooms_per_household","population_per_household"],
index=housing.index)
housing_extra_attribs.head()输出:
longitude latitude housing_median_age total_rooms total_bedrooms \
17606 -121.89 37.29 38 1568 351
18632 -121.93 37.05 14 679 108
14650 -117.2 32.77 31 1952 471
3230 -119.61 36.31 25 1847 371
3555 -118.59 34.23 17 6592 1525
population households median_income ocean_proximity rooms_per_household \
17606 710 339 2.7042 <1H OCEAN 4.62537
18632 306 113 6.4214 <1H OCEAN 6.00885
14650 936 462 2.8621 NEAR OCEAN 4.22511
3230 1460 353 1.8839 INLAND 5.23229
3555 4459 1463 3.0347 <1H OCEAN 4.50581
population_per_household
17606 2.0944
18632 2.70796
14650 2.02597
3230 4.13598
3555 3.04785 4.4 数据归一化
将数据喂入机器学习模型前通常需要做归一化操作,常用的归一化有两种:最小最大归一化和标准归一化。
- 属性值减去最小值再除以最大值,最终将所有值归一化到[0,1]范围内,离群值对这种方法影响大。sklearn中提供MinMaxScaler
- 属性值减去平均值再除以方差,最终数据转化成均值为0、方差为1的正态分布,而有将值限定到某一范围,离群值对这种方法影响小。sklearn中提供了StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
("imputer",SimpleImputer(strategy="median")),
("attribs_adder",CombinedAttributesAdder()),
("std_scaler",StandardScaler())
])
housing_num_tr = num_pipeline.fit_transform(housing_num)
housing_num_tr输出:
array([[-1.15604281, 0.77194962, 0.74333089, ..., -0.31205452,
-0.08649871, 0.15531753],
[-1.17602483, 0.6596948 , -1.1653172 , ..., 0.21768338,
-0.03353391, -0.83628902],
[ 1.18684903, -1.34218285, 0.18664186, ..., -0.46531516,
-0.09240499, 0.4222004 ],
...,
[ 1.58648943, -0.72478134, -1.56295222, ..., 0.3469342 ,
-0.03055414, -0.52177644],
[ 0.78221312, -0.85106801, 0.18664186, ..., 0.02499488,
0.06150916, -0.30340741],
[-1.43579109, 0.99645926, 1.85670895, ..., -0.22852947,
-0.09586294, 0.10180567]])sklearn0.20版本中加入了ColumnTransformer可以同时处理所有列
from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num) # 获取数值属性列名
cat_attribs = ["ocean_proximity"] # 获取类别属性列名
full_pipeline = ColumnTransformer([
("num",num_pipeline,num_attribs),
("cat",OneHotEncoder(),cat_attribs)
])
housing_prepared = full_pipeline.fit_transform(housing)
housing_prepared输出:
array([[-1.15604281, 0.77194962, 0.74333089, ..., 0. ,
0. , 0. ],
[-1.17602483, 0.6596948 , -1.1653172 , ..., 0. ,
0. , 0. ],
[ 1.18684903, -1.34218285, 0.18664186, ..., 0. ,
0. , 1. ],
...,
[ 1.58648943, -0.72478134, -1.56295222, ..., 0. ,
0. , 0. ],
[ 0.78221312, -0.85106801, 0.18664186, ..., 0. ,
0. , 0. ],
[-1.43579109, 0.99645926, 1.85670895, ..., 0. ,
1. , 0. ]])housing_prepared.shape输出:
(16512, 16)housing.shape输出:
(16512, 9)为什么最终是16列属性?数值类型的列是8列,类别属性1列变成5列的OneHot,再加上组合的rooms_per_household等三列属性,最终8+5+3=16列。
OneHotEncoder返回的是稀疏矩阵,而num_pipeline返回的密集矩阵,ColumnTransformer会对最终的矩阵进行密度评估:如果密度小于设置的阈值(默认为0.3)就会返回稀疏矩阵,否则会返回密集矩阵。
此案例中返回的是密集矩阵。可以进行一个大概的判断:num_pipeline处理的数字属性有8列,所有的都有值,而OneHotEncoder后的矩阵是5列,综合起来还是大部分是有值的,因此最终返回密集矩阵。
num_attribs输出:
['longitude',
'latitude',
'housing_median_age',
'total_rooms',
'total_bedrooms',
'population',
'households',
'median_income']cat_encoder.categories_输出:
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]5. 选择模型并训练
5.1 线性回归模型
选择线性回归模型进行训练
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)输出:
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)some_data = housing.iloc[:5]
some_labels = housing_labels[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("Predictions: ", lin_reg.predict(some_data_prepared))
print("Truth Labels: ", list(some_labels))输出:
Predictions: [210644.60459286 317768.80697211 210956.43331178 59218.98886849
189747.55849879]
Truth Labels: [286600.0, 340600.0, 196900.0, 46300.0, 254500.0]预测结果偏差好像有些大。
计算根均方误差看看:
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse) # np.sqrt()开平方根
lin_rmse输出:
68628.19819848923数据集中房价取值范围是120000至120000至265000,而均方根误差达到68628显然不是一个很好的结果,造成些的原因可能是模型欠拟合。
解决欠拟合主要有三个手段:选择更强的模型、喂入更多特征数据、减少对模型的约束。而在本案例中没有对模型进行任何约束,所以从前两个手段入手。
先尝试其它模型试试,例如决策树模型:
5.2 决策树模型
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(housing_prepared, housing_labels)输出:
DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=42, splitter='best')housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse输出:
0.0均方误差为0,不可能这么好运,很可能模型对训练数据进行了过度拟合。如何判断是否过拟合了,使用测试数据集测试一下就知道了,可是测试数据集一般是盖棺定论的时候用的,而更常用的方法是从训练集中分隔出一部分数据当作验证集。而验证集就是训练、调整模型超参数用的。
5.3 交叉验证
普通的做法是将训练集拆分成较小的训练集和验证集,再用拆分的训练集训练模型,用验证集评估模型。但sklearn中提供了更方便的工具:K折交叉验证(K-fold cross-validation):
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error",cv=10)
tree_rmse_scores = np.sqrt(-scores)sklearn交叉验证特征期望函数越大越好,而损失函数越小越好,交叉验证中的scoring函数与MSE函数相反,因此在scores前面加上负号。
def display_scores(scores):
print("Scores: ",scores)
print("Mean: ",scores.mean())
print("Standard deviation: ",scores.std())
display_scores(tree_rmse_scores)输出:
Scores: [70194.33680785 66855.16363941 72432.58244769 70758.73896782
71115.88230639 75585.14172901 70262.86139133 70273.6325285
75366.87952553 71231.65726027]
Mean: 71407.68766037929
Standard deviation: 2439.4345041191004可以看到,误差大概在71407左右,而前非像之前那么好(均方误差为0)。而且决策树的效果似乎还没有线性回归好,线性回归均方误差大概68628左右。
用线性回归试试交叉验证:
lin_scores = cross_val_score(lin_reg, housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)输出:
Scores: [66782.73843989 66960.118071 70347.95244419 74739.57052552
68031.13388938 71193.84183426 64969.63056405 68281.61137997
71552.91566558 67665.10082067]
Mean: 69052.46136345083
Standard deviation: 2731.67400179834255.4 随机森林模型
随机森林是集成算法中的一种,即随机生成多个决策树,最终取平均值。
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=100,random_state=42) # sklearn 0.22版本之后默认值为100
forest_reg.fit(housing_prepared, housing_labels)输出:
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=None, oob_score=False, random_state=42, verbose=0,
warm_start=False)housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse输出:
18603.515021376355很明显,随机森林的效果比之前两个模型都好。再通过交叉验证检查模型是否有过拟合现象:
from sklearn.model_selection import cross_val_score
forest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error",cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)输出:
Scores: [49519.80364233 47461.9115823 50029.02762854 52325.28068953
49308.39426421 53446.37892622 48634.8036574 47585.73832311
53490.10699751 50021.5852922 ]
Mean: 50182.303100336096
Standard deviation: 2097.0810550985693可以看到,训练集上的结果和验证集上的结果还是存在很大的差别,说明模型还是存在一定的过拟合。
5.5 支持向量机
from sklearn.svm import SVR
svm_reg = SVR(kernel="linear")
svm_reg.fit(housing_prepared, housing_labels)
housing_predictions = svm_reg.predict(housing_prepared)
svm_mse = mean_squared_error(housing_labels, housing_predictions)
svm_rmse = np.sqrt(svm_mse)
svm_rmse输出:
111094.6308539982以上输出可以发现,支持向量机模型误差太大,效果很差,说明支持向量机不太适合做线性回归的任务,而更合适做分类的任务。
6. 模型微调(Fine-Tune)
6.1 网络搜索(Grid Search)
基本思想:不断地尝试各种超参数组合,最终筛选出最佳超参数组合。sklearn提供了GridSearchCV工具可以自动化地完成这个工作。
from sklearn.model_selection import GridSearchCV
para_grid = [
{"n_estimators":[3,10,30],"max_features":[2,4,6,8]}, # 3*4=12种组合方式
{"bootstrap":[False],"n_estimators":[3,10],"max_features":[2,3,4]} # 1*2*3=6种组合方式
]
forest_reg = RandomForestRegressor(random_state=42)
grid_search = GridSearchCV(forest_reg, para_grid, cv=5,scoring="neg_mean_squared_error", # 每种组合方式进行折交叉验证
return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)输出:
GridSearchCV(cv=5, error_score='raise-deprecating',
estimator=RandomForestRegressor(bootstrap=True, criterion='mse',
max_depth=None,
max_features='auto',
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
n_estimators='warn', n_jobs=None,
oob_score=False, random_state=42,
verbose=0, warm_start=False),
iid='warn', n_jobs=None,
param_grid=[{'max_features': [2, 4, 6, 8],
'n_estimators': [3, 10, 30]},
{'bootstrap': [False], 'max_features': [2, 3, 4],
'n_estimators': [3, 10]}],
pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
scoring='neg_mean_squared_error', verbose=0)grid_search.best_params_输出:
{'max_features': 8, 'n_estimators': 30}grid_search.best_estimator_输出:
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features=8, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=30,
n_jobs=None, oob_score=False, random_state=42, verbose=0,
warm_start=False)cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score),params)输出:
63669.05791727153 {'max_features': 2, 'n_estimators': 3}
55627.16171305252 {'max_features': 2, 'n_estimators': 10}
53384.57867637289 {'max_features': 2, 'n_estimators': 30}
60965.99185930139 {'max_features': 4, 'n_estimators': 3}
52740.98248528835 {'max_features': 4, 'n_estimators': 10}
50377.344409590376 {'max_features': 4, 'n_estimators': 30}
58663.84733372485 {'max_features': 6, 'n_estimators': 3}
52006.15355973719 {'max_features': 6, 'n_estimators': 10}
50146.465964159885 {'max_features': 6, 'n_estimators': 30}
57869.25504027614 {'max_features': 8, 'n_estimators': 3}
51711.09443660957 {'max_features': 8, 'n_estimators': 10}
49682.25345942335 {'max_features': 8, 'n_estimators': 30}
62895.088889905004 {'bootstrap': False, 'max_features': 2, 'n_estimators': 3}
54658.14484390074 {'bootstrap': False, 'max_features': 2, 'n_estimators': 10}
59470.399594730654 {'bootstrap': False, 'max_features': 3, 'n_estimators': 3}
52725.01091081235 {'bootstrap': False, 'max_features': 3, 'n_estimators': 10}
57490.612956065226 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3}
51009.51445842374 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10}pd.DataFrame(grid_search.cv_results_)输出:
mean_fit_time std_fit_time mean_score_time std_score_time param_max_features param_n_estimators param_bootstrap params split0_test_score split1_test_score ... mean_test_score std_test_score rank_test_score split0_train_score split1_train_score split2_train_score split3_train_score split4_train_score mean_train_score std_train_score
0 0.0558 0.003544 0.0024 4.898819e-04 2 3 NaN {'max_features': 2, 'n_estimators': 3} -3.837622e+09 -4.147108e+09 ... -4.053749e+09 1.519609e+08 18 -1.064113e+09 -1.105142e+09 -1.116550e+09 -1.112342e+09 -1.129650e+09 -1.105559e+09 2.220402e+07
1 0.1714 0.001200 0.0076 4.898624e-04 2 10 NaN {'max_features': 2, 'n_estimators': 10} -3.047771e+09 -3.254861e+09 ... -3.094381e+09 1.327046e+08 11 -5.927175e+08 -5.870952e+08 -5.776964e+08 -5.716332e+08 -5.802501e+08 -5.818785e+08 7.345821e+06
2 0.5212 0.004996 0.0210 8.944157e-04 2 30 NaN {'max_features': 2, 'n_estimators': 30} -2.689185e+09 -3.021086e+09 ... -2.849913e+09 1.626879e+08 9 -4.381089e+08 -4.391272e+08 -4.371702e+08 -4.376955e+08 -4.452654e+08 -4.394734e+08 2.966320e+06
3 0.0826 0.000800 0.0030 0.000000e+00 4 3 NaN {'max_features': 4, 'n_estimators': 3} -3.730181e+09 -3.786886e+09 ... -3.716852e+09 1.631421e+08 16 -9.865163e+08 -1.012565e+09 -9.169425e+08 -1.037400e+09 -9.707739e+08 -9.848396e+08 4.084607e+07
4 0.2712 0.000980 0.0076 4.899014e-04 4 10 NaN {'max_features': 4, 'n_estimators': 10} -2.666283e+09 -2.784511e+09 ... -2.781611e+09 1.268562e+08 8 -5.097115e+08 -5.162820e+08 -4.962893e+08 -5.436192e+08 -5.160297e+08 -5.163863e+08 1.542862e+07
5 0.8270 0.006870 0.0214 1.019805e-03 4 30 NaN {'max_features': 4, 'n_estimators': 30} -2.387153e+09 -2.588448e+09 ... -2.537877e+09 1.214603e+08 3 -3.838835e+08 -3.880268e+08 -3.790867e+08 -4.040957e+08 -3.845520e+08 -3.879289e+08 8.571233e+06
6 0.1112 0.002993 0.0030 1.784161e-07 6 3 NaN {'max_features': 6, 'n_estimators': 3} -3.119657e+09 -3.586319e+09 ... -3.441447e+09 1.893141e+08 14 -9.245343e+08 -8.886939e+08 -9.353135e+08 -9.009801e+08 -8.624664e+08 -9.023976e+08 2.591445e+07
7 0.3696 0.002059 0.0078 3.998995e-04 6 10 NaN {'max_features': 6, 'n_estimators': 10} -2.549663e+09 -2.782039e+09 ... -2.704640e+09 1.471542e+08 6 -4.980344e+08 -5.045869e+08 -4.994664e+08 -4.990325e+08 -5.055542e+08 -5.013349e+08 3.100456e+06
8 1.1250 0.004733 0.0208 4.000187e-04 6 30 NaN {'max_features': 6, 'n_estimators': 30} -2.370010e+09 -2.583638e+09 ... -2.514668e+09 1.285063e+08 2 -3.838538e+08 -3.804711e+08 -3.805218e+08 -3.856095e+08 -3.901917e+08 -3.841296e+08 3.617057e+06
9 0.1398 0.001166 0.0026 4.900182e-04 8 3 NaN {'max_features': 8, 'n_estimators': 3} -3.353504e+09 -3.348552e+09 ... -3.348851e+09 1.241864e+08 13 -9.228123e+08 -8.553031e+08 -8.603321e+08 -8.881964e+08 -9.151287e+08 -8.883545e+08 2.750227e+07
10 0.4698 0.003544 0.0074 4.899598e-04 8 10 NaN {'max_features': 8, 'n_estimators': 10} -2.571970e+09 -2.718994e+09 ... -2.674037e+09 1.392720e+08 5 -4.932416e+08 -4.815238e+08 -4.730979e+08 -5.155367e+08 -4.985555e+08 -4.923911e+08 1.459294e+07
11 1.4162 0.008352 0.0210 6.324851e-04 8 30 NaN {'max_features': 8, 'n_estimators': 30} -2.357390e+09 -2.546640e+09 ... -2.468326e+09 1.091647e+08 1 -3.841658e+08 -3.744500e+08 -3.773239e+08 -3.882250e+08 -3.810005e+08 -3.810330e+08 4.871017e+06
12 0.0834 0.001356 0.0030 1.168008e-07 2 3 False {'bootstrap': False, 'max_features': 2, 'n_est... -3.785816e+09 -4.166012e+09 ... -3.955792e+09 1.900966e+08 17 -0.000000e+00 -0.000000e+00 -0.000000e+00 -0.000000e+00 -0.000000e+00 0.000000e+00 0.000000e+00
13 0.2742 0.001720 0.0086 4.898430e-04 2 10 False {'bootstrap': False, 'max_features': 2, 'n_est... -2.810721e+09 -3.107789e+09 ... -2.987513e+09 1.539231e+08 10 -6.056477e-02 -0.000000e+00 -0.000000e+00 -0.000000e+00 -2.967449e+00 -6.056027e-01 1.181156e+00
14 0.1076 0.002417 0.0032 4.000664e-04 3 3 False {'bootstrap': False, 'max_features': 3, 'n_est... -3.618324e+09 -3.441527e+09 ... -3.536728e+09 7.795196e+07 15 -0.000000e+00 -0.000000e+00 -0.000000e+00 -0.000000e+00 -6.072840e+01 -1.214568e+01 2.429136e+01
15 0.3522 0.003655 0.0086 4.899403e-04 3 10 False {'bootstrap': False, 'max_features': 3, 'n_est... -2.757999e+09 -2.851737e+09 ... -2.779927e+09 6.286611e+07 7 -2.089484e+01 -0.000000e+00 -0.000000e+00 -0.000000e+00 -5.465556e+00 -5.272080e+00 8.093117e+00
16 0.1316 0.002332 0.0032 3.999949e-04 4 3 False {'bootstrap': False, 'max_features': 4, 'n_est... -3.134040e+09 -3.559375e+09 ... -3.305171e+09 1.879203e+08 12 -0.000000e+00 -0.000000e+00 -0.000000e+00 -0.000000e+00 -0.000000e+00 0.000000e+00 0.000000e+00
17 0.4350 0.002608 0.0090 6.324851e-04 4 10 False {'bootstrap': False, 'max_features': 4, 'n_est... -2.525578e+09 -2.710011e+09 ... -2.601971e+09 1.088031e+08 4 -0.000000e+00 -1.514119e-02 -0.000000e+00 -0.000000e+00 -0.000000e+00 -3.028238e-03 6.056477e-03
18 rows × 23 columns通过GridSearch得出最佳的两参数,8和30组合时mean_scores为49682,比之前的50182效果要好。
但稍加观察可以发现这两个数都是候选值中最大的,即边缘值,也就说继续增大参数选择,可能会找到更优的参数。
尝试更佳参数选择:
para_grid = [
{"n_estimators":[30,50,80],"max_features":[8,10,12,14]}, # 3*4=12种组合方式
{"bootstrap":[False],"n_estimators":[20,30,80],"max_features":[4,8,12,14]} # 1*3*4=12种组合方式
]
forest_reg = RandomForestRegressor(random_state=42)
grid_search = GridSearchCV(forest_reg, para_grid, cv=5,scoring="neg_mean_squared_error", # 每种组合方式进行折交叉验证
return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)输出:
GridSearchCV(cv=5, error_score='raise-deprecating',
estimator=RandomForestRegressor(bootstrap=True, criterion='mse',
max_depth=None,
max_features='auto',
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
n_estimators='warn', n_jobs=None,
oob_score=False, random_state=42,
verbose=0, warm_start=False),
iid='warn', n_jobs=None,
param_grid=[{'max_features': [8, 10, 12, 14],
'n_estimators': [30, 50, 80]},
{'bootstrap': [False], 'max_features': [4, 8, 12, 14],
'n_estimators': [20, 30, 80]}],
pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
scoring='neg_mean_squared_error', verbose=0)grid_search.best_params_输出:
{'bootstrap': False, 'max_features': 8, 'n_estimators': 80}grid_search.best_estimator_输出:
RandomForestRegressor(bootstrap=False, criterion='mse', max_depth=None,
max_features=8, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=80,
n_jobs=None, oob_score=False, random_state=42, verbose=0,
warm_start=False)从上述输出结果可以看出,max_features可能8就是最佳参数,而n_estimators继续增大时可能会更好。
6.2 随机搜索
当超参数搜索空间很大时,即参数组合很多时,使用GridSearch进行搜索就显得非常吃力,此时随机搜索就比较有用。
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
para_distribs = {
"n_estimators":randint(low=1,high=200),
"max_features":randint(low=1,high=8)
}
forest_reg = RandomForestRegressor(random_state=42)
rnd_search = RandomizedSearchCV(forest_reg,param_distributions=para_distribs,
n_iter=10, cv=5, scoring="neg_mean_squared_error",
random_state=42)
rnd_search.fit(housing_prepared, housing_labels)输出:
RandomizedSearchCV(cv=5, error_score='raise-deprecating',
estimator=RandomForestRegressor(bootstrap=True,
criterion='mse',
max_depth=None,
max_features='auto',
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
n_estimators='warn',
n_jobs=None, oob_score=False,
random_sta...
warm_start=False),
iid='warn', n_iter=10, n_jobs=None,
param_distributions={'max_features': ,
'n_estimators': },
pre_dispatch='2*n_jobs', random_state=42, refit=True,
return_train_score=False, scoring='neg_mean_squared_error',
verbose=0) cvres = rnd_search.cv_results_
for mean_score, param in zip(cvres["mean_test_score"],cvres["params"]):
print(np.sqrt(-mean_score),param)输出:
49150.657232934034 {'max_features': 7, 'n_estimators': 180}
51389.85295710133 {'max_features': 5, 'n_estimators': 15}
50796.12045980556 {'max_features': 3, 'n_estimators': 72}
50835.09932039744 {'max_features': 5, 'n_estimators': 21}
49280.90117886215 {'max_features': 7, 'n_estimators': 122}
50774.86679035961 {'max_features': 3, 'n_estimators': 75}
50682.75001237282 {'max_features': 3, 'n_estimators': 88}
49608.94061293652 {'max_features': 5, 'n_estimators': 100}
50473.57642831875 {'max_features': 3, 'n_estimators': 150}
64429.763804893395 {'max_features': 5, 'n_estimators': 2}随机搜索出10组超参数组合。
6.3 分析最佳模型
feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances输出:
array([7.58744378e-02, 6.78499428e-02, 4.19007228e-02, 1.48764231e-02,
1.38685455e-02, 1.41736267e-02, 1.38318766e-02, 3.70241621e-01,
4.89380985e-02, 1.10122210e-01, 5.43566571e-02, 5.97927301e-03,
1.62816474e-01, 7.91378906e-05, 2.11403803e-03, 2.97691572e-03])extra_attribs = ["rooms_per_hhold","pop_per_hhold","bedrooms_per_room"]
cat_encoder = full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs +extra_attribs+cat_one_hot_attribs
sorted(zip(feature_importances,attributes),reverse=True)输出:
[(0.3702416205722281, 'median_income'),
(0.16281647391862586, 'INLAND'),
(0.11012221006942573, 'pop_per_hhold'),
(0.07587443781723896, 'longitude'),
(0.06784994279359013, 'latitude'),
(0.05435665711948978, 'bedrooms_per_room'),
(0.04893809850661322, 'rooms_per_hhold'),
(0.041900722751888345, 'housing_median_age'),
(0.014876423067328884, 'total_rooms'),
(0.014173626700600368, 'population'),
(0.01386854546599152, 'total_bedrooms'),
(0.013831876573763422, 'households'),
(0.005979273010634567, '<1H OCEAN'),
(0.00297691571669059, 'NEAR OCEAN'),
(0.0021140380252633183, 'NEAR BAY'),
(7.913789062714212e-05, 'ISLAND')]
以上输出显示了属性或特征的重要性,可以看到很多特征的重要性很低,可以考虑将这些特征删除掉,以减轻模型负担。
同时需要检查模型错误率,并尝试分析错误发生在什么地方:
final_model = grid_search.best_estimator_
X_test = strat_test_set.drop("median_house_value",axis=1)
y_test = strat_test_set["median_house_value"].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse输出:
46736.13265618231from scipy import stats
confidence = 0.95
squared_errors = (final_predictions - y_test)**2
np.sqrt(stats.t.interval(confidence, len(squared_errors)-1,
loc=squared_errors.mean(),
scale=stats.sem(squared_errors)))输出:
array([44718.52821289, 48670.16977354])# 手动计算方式:
m = len(squared_errors)
mean = squared_errors.mean()
tscore = stats.t.ppf((1+confidence)/2,df=m-1)
tmargin = tscore*squared_errors.std(ddof=1)/np.sqrt(m)
np.sqrt(mean-tmargin),np.sqrt(mean+tmargin)输出:
(44718.52821289402, 48670.16977353933)# 也可以使用z-scores代替t-scores:
zscore = stats.norm.ppf((1+confidence)/2)
zmargin = zscore*squared_errors.std(ddof=1)/np.sqrt(m)
np.sqrt(mean-zmargin),np.sqrt(mean+zmargin)输出:
(44719.133276515044, 48669.61382947091)7. 部署、监视并维护模型系统
保存训练的模型,包括全部的预处理过程、预测pipeline等,然后部署到生产环境中进行预测。
可以将模型部署在专用服务器上,也可以部署在云平台上,例如Google AI云平台。