学习记录--SWPU青云杯

1. 7-1 单词翻转（10分）
2. 7-2 装箱问题（10分）
3. 7-3 玩转完全平方数 (15 分)
4. 7-4 列车调度 (20 分)
5. 7-5 完全二叉树的层序遍历 (20 分)
6. 7-6 球队“食物链” (25 分)

1 . 7-1 单词翻转（10分）

问题描述
输入一个句子（一行），将句子中的每一个单词翻转后输出。

输入描述
只有一行，为一个字符串，不超过500个字符。单词之间以空格隔开。

输出描述
翻转每一个单词后的字符串，单词之间的空格需与原文一致。

样例输入1

hello world

样例输出1：

olleh dlrow

样例输入2：

li   hai   la      wo   de      guo

样例输出2：

il   iah   al      ow   ed      oug

代码：

#include
using namespace std;
string s;
void solve()
{
   for(int i=0;i<s.length();i++)
   {
     
       if(s[i]!=' ')
	   {
	   	  int p1=i,p2=i;
	   	  while(s[p2]!=' ' && p2<s.length())
	   	  {
	   	    p2++; 	
		  }
		  p2--;
		  for(int j=p2;j>=p1;j--)
		    cout<<s[j];
		 i=p2;
	   }   	
	   else 
	     cout<<s[i];
  }	
}
int main()
{
	getline(cin,s);
	solve(); 
  return 0;
} 

2 . 7-2 装箱问题（10分）

假设有N项物品，大小分别为s1,s2,…,sn,其中si满足(si>=1 && si<=100)的整数。要把这些物品装入到容量为100的一批箱子（序号1-N）中。装箱方法是：对每项物品, 顺序扫描箱子，把该物品放入足以能够容下它的第一个箱子中。请写一个程序模拟这种装箱过程，并输出每个物品所在的箱子序号，以及放置全部物品所需的箱子数目。

输入格式：输入第一行给出物品个数N（<=1000）;第二行给出N个正整数Si(Si>=1 && Si<=100,表示第i项物品的大小)
输出格式：

按照输入顺序输出每个物品的大小及其所在的箱子序号，每个物品占1行，最后一行输出所需的箱子数目。
输入样例：

8
60 70 80 90 30 40 10 20

输出样例：

60 1
70 2
80 3
90 4
30 1
40 5
10 1
20 2
5

代码：

#include
using namespace std;
int n;
int a[1001];
int b[1001];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
	    cin>>a[i];
	    b[i]=100;
	}
	int k=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(b[j]>=a[i])
			{
				if(b[j]==100)
				  k++;
				cout<<a[i]<<' '<<j<<endl;
				b[j]-=a[i];
				break; 
			}
		}
	}
	cout<<k;
	return 0;
	 
	
}

3 . 7-3 玩转完全平方数 (15 分)

一个整数 a是一个完全平方数，是指它是某一个整数的平方，即存在一个整数 b，使得a=b*。
给定一个正整数 n，请找到最小的正整数 x，使得它们的乘积是一个完全平方数。
输入格式:
输入一行包含一个正整数 n。

输出格式:
输出找到的最小的正整数 x。
数据范围（需要开long long ）
输入样例1:

12

输出样例1:

3

输入样例2:

666

输出样例2:

74

输入样例3:

12345678

输出样例3:

1371742

**思路：**其实就是一道数学题（当时没想到），先从最小的i=2开始，
对于数n的每一层，若要使nx=bb;则每一层都必须是2*k个i相乘，否则对最后的输出ans *i。
代码：

#include
using namespace std;
typedef long long ll;
ll n;
void solve()
{
	ll ans=1;
	ll i=2;
	while(i*i<=n)
	{
		int k=0;
		while(n%i==0)
		{
			k++;
			n/=i;
		}
		if(k%2)
		  ans*=i;
		i++;
	}
	if(n>1)
	  ans*=n;//类似于处理边界
	cout<<ans; 
}
int main()
{
	cin>>n;
	solve();
	return 0;
}

4 . 7-4 列车调度 (20 分)

火车站的列车调度铁轨的结构如下图所示。

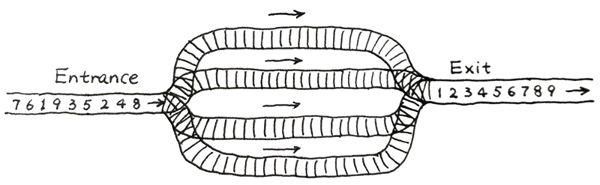
两端分别是一条入口（Entrance）轨道和一条出口（Exit）轨道，它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入，最后从出口离开。在图中有9趟列车，在入口处按照{8，4，2，5，3，9，1，6，7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开，则至少需要多少条平行铁轨用于调度？

输入格式：
输入第一行给出一个整数N[1,1e5],下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。
输出格式：
在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。
输入样例：

9
8 4 2 5 3 9 1 6 7

输出样例：

4

思路：每次插入一个数前，把小于它的数全部删掉，n次操作后，集合里元素的个数即为ans
代码：

#include
using namespace std;

set<int>a;
int n;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		if(a.lower_bound(x)!=a.end())
		  a.erase(a.upper_bound(x));
		a.insert(x);
	}
	cout<<a.size();
	return 0;
	
}

5 . 7-5 完全二叉树的层序遍历 (20 分)

题意：给出一颗N个节点的数，求其层次遍历（简单的递归建树）
代码：

#include
using namespace std;
int n;
int t[1001];
void built(int l,int r,int i)
{
	if(i>n)
	  return;
	int mid=(l+r)>>1;
	if(l<=mid)
	  built(l,mid,i*2);
	if(mid+1<=r)
	  built(mid+1,r-1,i*2+1);
     cin>>t[i];
     
}
int main()
{
	cin>>n;
	built(1,n,1);
	for(int i=1;i<=n;i++)
	{
	    cout<<t[i];
	    if(i!=n)
		  cout<<' '; 
	}
	  
	return 0;
}

6 . 7-6 球队“食物链” (25 分)

某国的足球联赛中有N支参赛球队，编号从1至N。联赛采用主客场双循环赛制，参赛球队两两之间在双方主场各赛一场。

联赛战罢，结果已经尘埃落定。此时，联赛主席突发奇想，希望从中找出一条包含所有球队的“食物链”，来说明联赛的精彩程度。“食物链”为一个1至N的排列{T1,T2,…Tn},满足：球队T1战胜过T2球队，T2球队战胜过T3球队…，Tn战胜过T1球队。现在主席请你从联赛结果中找出“食物链”。若存在多条“食物链”，请找出字典序最小的。

输入格式：
输入第一行给出一个整数N[1,20],，为参赛球队数。随后N行，每行N个字符，给出了N×N的联赛结果表，其中第i行第j列的字符为球队i在主场对阵球队j的比赛结果：W表示球队i战胜球队j，L表示球队i负于球队j，D表示两队打平，-表示无效（当i=j时）。输入中无多余空格。

输出格式：
按题目要求找到“食物链“T1,T2,T3…Tn,将这N个数依次输出在一行上，数字间以1个空格分隔，行的首尾不得有多余空格。若不存在“食物链”，输出“No Solution”。

输入样例1：

5
-LWDW
W-LDW
WW-LW
DWW-W
DDLW-

输出样例1：

1 3 5 4 2

输入样例2：

5
-WDDW
D-DWL
DD-DW
DDW-D
DDDD-

No Solution

思路:…直接可以爆搜（加一点剪枝）
代码：

#include
using namespace std;
bool e[202][202];
int n;
bool vis[202];
vector<int>a;
bool flag=0;
bool pd()
{
	for(int i=2;i<=n;i++)
	{
	
      	if(!vis[i] && e[i][1])
      	  return 1;
    }
	return 0;  
}
void dfs(int pre)
{
	if(a.size()==n)
	{
		flag=1;
		return;
	}
	if(flag || !pd())
	  return;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i] && e[pre][i])
		{
			vis[i]=1;
			a.push_back(i);
			dfs(i);
			if(flag)
			  return;
			a.pop_back();
			vis[i]=0;
		}
	}
}
int main()
{
	cin>>n;
	char c;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>c;
			if(c=='W')
			  e[i][j]=1;
			if(c=='L')
			  e[j][i]=1;
		}
	}
	a.push_back(1);
	vis[1]=1;
	dfs(1);
	if(flag)
	{
		for(int i=0;i<n;i++)
		 {
		 	if(i)
		 	  cout<<' ';
		 	cout<<a[i];
		  } 
	}
	else 
	  cout<<"No Solution";
	return 0;
	
}

Con:我太菜了…
mood: