机器学习笔记(四)BP神经网络模型

写完才感觉自己可能用了很多术语= =大家听不懂就问就行，我之前可能写过但是很杂，我自己都感觉写的太乱了= =。
笔记参考：方巍的Python数据挖掘与机器学习实战

1、基础概念

人工神经网络的概念：其从信息处理角度对人脑神经元网络进行抽象，构建某种简单的模型，按不同的连接方式组成不同的网络。在工程与学术界我们通常把人工神经网络简称为神经网络或类神经网络。

神经网络的概念：是一种运算模型，由大量的节点(也可以说神经元)之间连接构成。每个节点代表一种特定的输出函数，称为激励函数或者激活函数。每两个节点间的连接都代表一个对于通过连接信号的加权值，称之为权重。这相当于人神经的记忆(就是仿生)，神经网络的输出则根据网络的连接方式、权重值和激活函数的不同而不同。而网络本身通常都是对自然界某种算法或函数的逼近，也可能是一种逻辑策略的表达。简单来说，人工神经网络搭建利用函数拟合的性质体现自然规律。

2、结构特点

人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统。具有四个特征。

• 非线性 ：人工神经元处于激活或抑制两种不同的状态，这种行为在数学上表现为一种非线性关系。
• 非局限性：一个神经网络一般由很多神经元组成。一个系统的整体行为不仅取决于单个神经元的特征，而且由单元之间相互作用，相互连接组成，通过单元之间的大量连接模拟大脑的非局限性。
• 非常定性：处理信息的时候，信息可以有各种变化，非线性动力系统本身也在变化，通常用迭代描述这个动力系统的过程。（可以用EM去理解）
• 非凸性：一个系统的演化方向，在一定条件下取决于某个特定的状态函数。

3、网络模型

目前有很多种神经网络模型，这里说下四种

• 前向型：网络中各个神经元接受前一级的输入，并输出到下一级，网络中没有反馈，可以用一个有向无环路图表示。
• 反馈型：网络内神经元有反馈，可以用一个无向的完备图表示。
• 随机型：具有随机性质的模拟退火(SA)算法解决了优化计算过程陷于局限性极小的问题。
• 竞争型：自组织神经网络模拟人脑行为，根据过去经验自动适应周围的环境变化，由于无监督通常采用竞争原则进行网络学习和自动聚类。

4、人工神经网络简介

主要说一下传统神经网络的基本组成部分和前向传播等内容。

4.1、神经元

高中生物上学过(对文科生抱歉= =这个俺真没法讲明白)，一个神经元有多个树突主要用来接受传入信息，轴突只有一条，轴突尾端有许多轴突末梢可以给其他多个神经元传递信息。轴突末梢跟其他神经元的树突产生连接，从而传递信号。这就是突触。

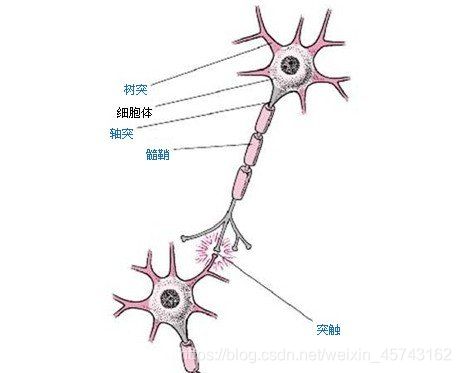
图片来自：http://keertech.blog.ifeng.com/article/29465278.html

神经元模型是一个包含输入、输出与计算功能的模型。具体可以类比人体的神经元。神经元可以使用任何标准函数来处理数据，这些函数就叫激活函数(需要这些函数磕到而且光滑)。一个个神经元连成一个神经网络。

4.2、单层神经网络

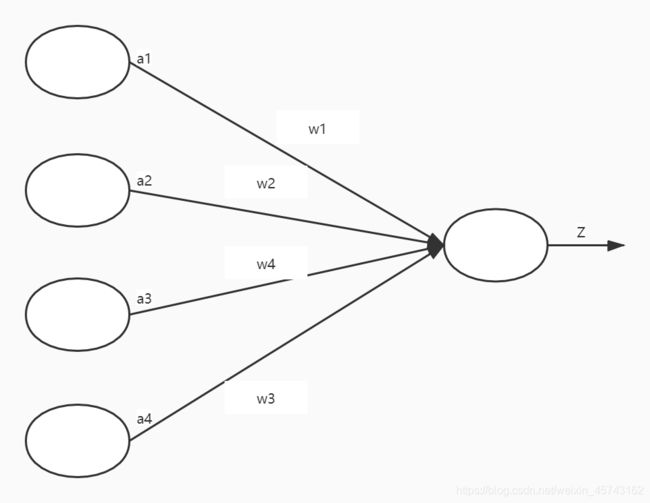
这里神经元是由a1、a2、a3、a4作为输入，w1、w2、w3、w4是权重，输入节点后经过激活节点，输出z，中间那一个激活节点的函数就是激活函数。
我们来看一下sigmoid函数：
f(z) = 1 / (1 + exp(-z))

对于上图： g(W^T*a) = z
W就是[w1,w2,w3,w4]
a是[a1,a2,a3,a4]

4.3、双层神经网络

单层神经元无法解决异或问题，所以我们可以加一给计算层，而且还具有很好的非线性分类效果，但是两层神经网络的计算是个问题。但是这时候我们就可以用BP来解决两层神经网络所需要的复杂计算量问题。两层神经网络除了包含输入层和输出层外还增加了一个中间层，这时候中间层和输出层都是计算层。

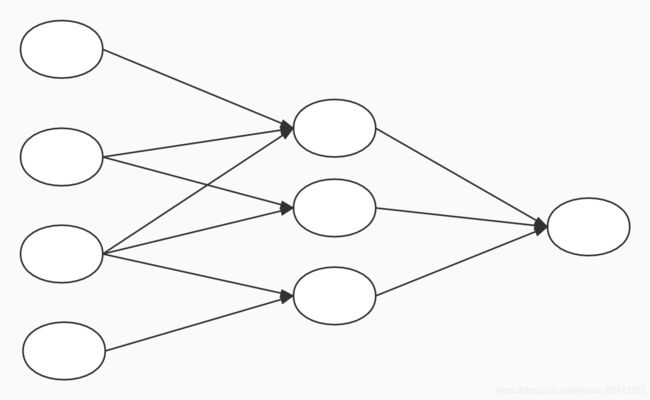
以上就是双层神经网络的格式，中间那个就是中间层。

中间层的节点是默认存在的，它本质上是一个只含有存储功能，且存储值永远为1的单元。在神经网络的每个层次中，除了输出层，都会有一个偏置单元。也就是咱们常说的y = wx + b的b。
所以，每一次神经元的计算可以写成如下：
g(W*a + b) = z

与单层神经网络不同。两层神经网络可以无限逼近任意连续函数。也就是说，面对复杂的非线性分类任务，两层神经网络可以很好的分类。

4.4、多层神经网络

既然有单层神经网络，双层神经网络，现在也存在多层神经网络。Hinton在2006年提出深度信念网络与传统神经网络的不同点在于，多层神经网络有一个预训练的过程，方便神经网络的权值找到一个最优解，之后不断微调，对整个网络进行训练。大幅度减少了寻变脸多层神经网络的时间。
也是一层层进行计算。有点像向前不断推进的感觉，这个过程也叫正向传播。
多层神经网络有什么好处？
能够使神经网络有更强的表现函数的能力。(比如第一层学到的是点的特征，第二层就是学到的是由点组成的线的特征，第三层就是由线组成的面的特征)

5、Bp神经网络

Bp神经网络是一种非线性多层前向反馈网络，一般分三层，分别是输入层、隐含层和输出层，这三层中的每一层只影响下一层的神经元状态，若预期预测结果得不到期望输出，网络则进行反向传播。
主要思路：输入数据，利用反向传播算法不断调整参数，根据最终调整的参数建立模型。
下面是Bp神经网络拓扑结构，来源于百度百科：

图中输入值为X1,X2…Xn,输出值为Y1,Y2,…,Ym,权值为V、W.由图可以看出神经网络是从n个自变量到m个因变量的映射过程。
具体步骤：

1. 初始化网络，通过输入样本来确定输入的维数(n)，输出的维数(m)。初始化输入层、隐含层和输出层神经元之间的权值V、W,初始化隐含层和输出阈值，并设置学习率和激活函数。

2. 计算隐含层输出:
   H_j = f(Σⁿ_i=1 ш_ijx_i+a_j),j = 1,2,…,I
   其中X表示输入变量，ш_ij、a_j表示输入层和隐含层间的连接权值及隐含层阈值，隐含层输出为H，I是隐含层节点数，f为隐含层激活函数。

3. 计算输出层：
   Y_k = Σ^I_j=1H_j ш_jk+b_k,k = 1,2…,m
   其中ш_jkb分别是连接权值和阈值。

4. 计算误差，误差e的计算为(也就是验证集的作用)
   e_k = Y_k - O_k,k=1,2,…m
   Y_k是预测值，O_k也就是实际期望的值。

5. 更新权值和阈值，通过预测误差e对网络连接权值更新。
   ш_ij = ш_ij+лH_j(1-H_j)x_iΣ^m_k=1ш_jke_k,i=1,2,…,n;j=1,2,…,I
   ш_jk=ш_jk+лH_je_k,j=1,2…,I;k=1,2,…m
   a_j = a_j +лH_j(1-H_j)Σ^m_k=1ш_jke_k,j=1,2,…,I
   b_k = b_k+ лe_k,k=1,2,…m
   其中л是学习率

6. 判断迭代是否可以结束，如果没有结束，就返回第(2)步，直到算法结束。

ps：前三步是信号前馈过程，第(4)步到第(7)步是神经网络反向更新参数的过程。

6、实战

#构建一个结构为[10,15,1]的BP神经网络
model = tf.keras.Sequential([tf.keras.layers.Dense(15,activation='relu',input_shape=(10,)),
                             tf.keras.layers.Dense(1)])
model.summary()  #显示网络结构
model.compile(optimizer='SGD',loss='mse')  #定义优化方法为随机梯度下降，损失函数为mse
#x->训练集,y——>bia标签,epochs=10000训练的次数,validation_data=(test_x,test_y)——>验证集
history = model.fit(x,y,epochs=10000,validation_data=(test_x,test_y))