第十三届蓝桥杯大赛软件赛省赛(Java 大学A组)
蓝桥杯 2022年省赛真题
Java 大学A组
- 试题 A: 裁纸刀
- 试题 B: 寻找整数
- 试题 C: 求和
- 试题 D: GCD
- 试题 E: 蜂巢
- 试题 F: 全排列的价值
- 试题 G: 青蛙过河
- 试题 H: 因数平方和
- 试题 I: 最优清零方案
- 试题 J: 推导部分和
小做一会 J A \mathrm{JA} JA 打发时间。
试题 A: 裁纸刀
本题总分: 5 5 5 分
【问题描述】
小蓝有一个裁纸刀,每次可以将一张纸沿一条直线裁成两半。
小蓝用一张纸打印出两行三列共 6 6 6 个二维码,至少使用九次裁出来,下图给出了一种裁法。

在上面的例子中,小蓝的打印机没办法打印到边缘,所以边缘至少要裁 4 4 4 次。另外,小蓝每次只能裁一张纸,不能重叠或者拼起来裁。
如果小蓝要用一张纸打印出 20 20 20 行 22 22 22 列共 440 440 440 个二维码,他至少需要裁多少次?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
443
我们可以仿照两行三列时,题目给出的切分法,写出一个递归程序去计算它的切割次数,
题目给出的方法可以抽象为两部分,
1 、 1、 1、边缘裁剪 4 4 4 次。
2 、 2、 2、选择当前纸片中连接二维码数量最多的一条线,沿其切割,分割成两个小纸片,重复此步直至纸片的某行或某列为 1 1 1。
public class Test {
public static void main(String[] args) { System.out.println(calc(20, 22) + 4); }
static int calc(int row, int col) {
if (row > col) return calc(col, row);
if (col == 1) return row - 1;
if (row == 1) return col - 1;
if (row % 2 == 0) return 2 * calc(row / 2, col) + 1;
return calc(1, col) + 2 * calc(row / 2, col) + 2;
}
}
当然这种方式并非绝对最优,一种较为稳妥的方式是在记忆化处理下暴搜,不过总所周知,记忆化搜索是状压 d p \mathrm{dp} dp 的递归实现,由此,我们可以在状态转移方程上研究出最优方案之间的共性,
设状态 f i , j f_{i,j} fi,j 为 i i i 行 j j j 列的纸片在最优裁剪方案下的步骤数,显然有 f i , j = f j , i f_{i,j} = f_{j,i} fi,j=fj,i、 f i , 1 = i − 1 f_{i,1} = i-1 fi,1=i−1、 f i , j = min { f i ′ , j + f i − i ′ , j , f i , j ′ + f i , j − j ′ } + 1 ∣ 1 ≤ i ′ < i , 1 ≤ j ′ < j f_{i,j}=\min\{f_{i',j}+f_{i-i',j},f_{i,j'} +f_{i,j-j'}\}+1|1\leq i' < i,1\leq j' < j fi,j=min{fi′,j+fi−i′,j,fi,j′+fi,j−j′}+1∣1≤i′<i,1≤j′<j,
当我们知道 f i ′ , j + f i − i ′ , j f_{i',j}+f_{i-i',j} fi′,j+fi−i′,j、 f i , j ′ + f i , j − j ′ f_{i,j'} +f_{i,j-j'} fi,j′+fi,j−j′ 中谁更优时,不妨假设当 i + j = k + g i+j=k+g i+j=k+g 时 f i , j = f k , g f_{i,j} = f_{k,g} fi,j=fk,g,
我们将 f i , j f_{i,j} fi,j 的表达式变形为 f i , j = min { f i ′ , j + f i − i ′ , j + 1 , f i , j ′ + f i , j − j ′ + 1 } − 1 f_{i,j}=\min\{f_{i',j}+f_{i-i',j}+1,f_{i,j'} +f_{i,j-j'}+1\}-1 fi,j=min{fi′,j+fi−i′,j+1,fi,j′+fi,j−j′+1}−1,将 f i , 1 = i − 1 f_{i,1} = i-1 fi,1=i−1 代入式中会发现,无论怎么拆分,最后表达式一定是若干 f 1 , x + 1 f_{1,x}+1 f1,x+1、 f y , 1 + 1 f_{y,1}+1 fy,1+1 和 − 1 -1 −1 的累加,其和一定是 i × j − 1 i×j-1 i×j−1。
耶,我们证明切分次数与切分方案无关,
太棒了,草
试题 B: 寻找整数
本题总分: 5 5 5 分
【问题描述】
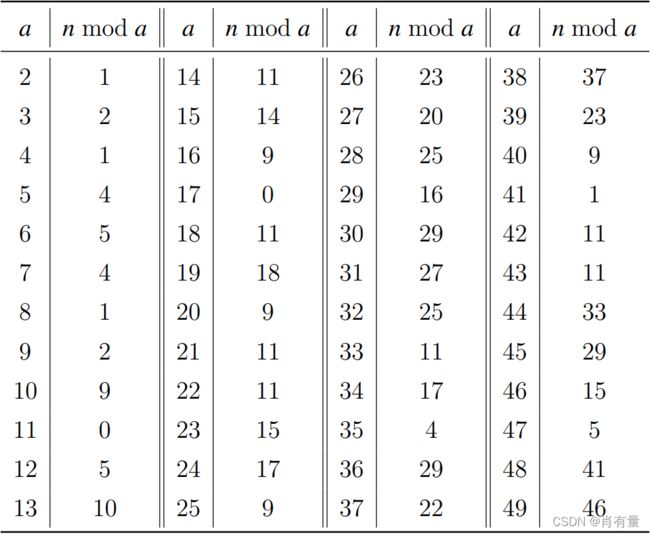
有一个不超过 1 0 17 10^{17} 1017 的正整数 n n n,知道这个数除以 2 2 2 至 49 49 49 后的余数如下表所示,求这个正整数最小是多少。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
2022040920220409
扩展中国剩余定理
对于一元线性同余方程组 : : : { x ≡ r 1 ( m o d n 1 ) x ≡ r 2 ( m o d n 2 ) ⋮ x ≡ r k ( m o d n k ) \begin{cases} x &\equiv r_1 \pmod {n_1} \\ x &\equiv r_2 \pmod {n_2} \\ &\ \vdots \\ x &\equiv r_k \pmod {n_k} \\ \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧xxx≡r1(modn1)≡r2(modn2) ⋮≡rk(modnk) 方程组的唯一是 x = ∑ i = 1 k r i m i i n v ( m i , n i ) ( m o d M ) x = \sum_{i=1}^kr_im_i\mathrm{inv}(m_i,n_i)\pmod M x=∑i=1krimiinv(mi,ni)(modM),其中 M = ∏ i = 1 k n 1 M = \prod_{i=1}^kn_1 M=∏i=1kn1, m i = M n i m_i = \frac{M}{n_i} mi=niM, i n v ( a , b ) \mathrm{inv}(a,b) inv(a,b) 为 a − 1 ( m o d b ) a^{-1}\pmod b a−1(modb)。
可是对于 gcd ( m i , n i ) ≠ 1 \gcd(m_i,n_i)\neq1 gcd(mi,ni)=1 的情况, i n v ( m i , n i ) \mathrm{inv}(m_i,n_i) inv(mi,ni) 不存在,此时无法使用 C R T \mathrm{CRT} CRT 求解。
于是引入扩展中国剩余定理 ( E X C R T ) : \mathrm{(EXCRT)}: (EXCRT):
对于 k = 2 k=2 k=2,即方程组为 : : : { x ≡ r 1 ( m o d n 1 ) x ≡ r 2 ( m o d n 2 ) \begin{cases}x&\equiv r_1 \pmod {n_1} \\ x &\equiv r_2 \pmod {n_2} \\ \end{cases} {xx≡r1(modn1)≡r2(modn2) 我们将 x x x 化为不定方程 x = n 1 p + r 1 = n 2 q + r 2 x=n_1p+r_1=n_2q+r_2 x=n1p+r1=n2q+r2,移项后有 n 1 p − n 2 q = r 2 − r 1 n_1p-n_2q=r_2-r_1 n1p−n2q=r2−r1,若 gcd ( n 1 , n 2 ) ∣ ( r 2 − r 1 ) \gcd(n_1,n_2)|(r_2-r_1) gcd(n1,n2)∣(r2−r1),另 k = n 1 gcd ( n 1 , n 2 ) k =\frac{n_1}{\gcd(n_1,n_2)} k=gcd(n1,n2)n1、 g = n 2 gcd ( n 1 , n 2 ) g =\frac{n_2}{\gcd(n_1,n_2)} g=gcd(n1,n2)n2,容易使用 E X G C D \mathrm{EXGCD} EXGCD 找到一组 p , q p,q p,q 使得 k p + q g = 1 kp+qg=1 kp+qg=1,此时 x ∗ = n 1 p + r 1 = r 2 − r 1 gcd ( n 1 , n 2 ) p + r 1 x^*=n_1p+r_1=\frac{r_2-r_1}{\gcd(n_1,n_2)}p+r_1 x∗=n1p+r1=gcd(n1,n2)r2−r1p+r1 同时满足两式。
当然题目中的方程数列为 48 48 48,我们需要将 x x x 推广到更一般的形式来计算出满足全部方程的 x x x,若 x x x 存在,容易对满足 x ≡ r 1 ( m o d n 1 ) x\equiv r_1 \pmod{n_1} x≡r1(modn1)、 x ≡ r 2 ( m o d n 2 ) x\equiv r_2 \pmod{n_2} x≡r2(modn2) 的特解 x ∗ = n 1 p + r 1 x^* = n_1p+r_1 x∗=n1p+r1 构造出平凡解系 x ∗ + k l c m ( n 1 , n 2 ) x^* + k\mathrm{lcm}(n_1,n_2) x∗+klcm(n1,n2),将两式化为一元线性同余方程 x ≡ x ∗ ( m o d l c m ( n 1 , n 2 ) ) x \equiv x^* \pmod{\mathrm{lcm}(n_1,n_2)} x≡x∗(modlcm(n1,n2))。
这个结论是显然的,但在此之上还有个推论就是一个完全剩余系中有且仅有一个解,
不想证,摆了。
不过这题用 J a v a \mathrm{Java} Java 实现起来较为恶心,因为 ( 1 , 49 ] (1,49] (1,49] 中的质数有 15 15 15 个,粗劣估计它们的乘积一定是会爆 long,
叹息。
import java.math.BigInteger;
public class Test {
public static void main(String[] args) { new Test().run(); }
int[] R = { 0, 0, 1, 2, 1, 4, 5, 4, 1, 2, 9, 0, 5, 10, 11, 14, 9, 0, 11, 18, 9, 11, 11, 15, 17, 9, 23, 20, 25, 16, 29, 27, 25, 11, 17, 4, 29, 22, 37, 23, 9, 1, 11, 11, 33, 29, 15, 5, 41, 46 };
void run() {
BigInteger M = BigInteger.valueOf(2), r = BigInteger.ONE;
for (int i = 3; i <= 49; ++i) {
BigInteger d = exgcd(M, BigInteger.valueOf(i));
exgcd(M.divide(d), BigInteger.valueOf(i).divide(d));
r = r.add(BigInteger.valueOf(R[i]).subtract(r).divide(d).multiply(p).multiply(M));
M = lcm(M, BigInteger.valueOf(i));
r = r.mod(M);
}
System.out.println(r);
}
BigInteger p, q;
BigInteger exgcd(BigInteger a, BigInteger b) {
if (b.equals(BigInteger.ZERO)) {
q = BigInteger.ZERO;
p = BigInteger.ONE;
return a;
}
BigInteger d = exgcd(b, a.mod(b));
BigInteger k = p;
p = q;
q = k.subtract(a.divide(b).multiply(q));
return d;
}
BigInteger lcm(BigInteger a, BigInteger b) { return a.multiply(b).divide(exgcd(a, b)); }
}
也可以在 long 被爆掉之前停下,用当前的 a ∗ a^* a∗ 暴力的搜索 k a ∗ ka^* ka∗, k a ∗ ka^* ka∗ 符合同余方程组且 k k k 最小。
试题 C: 求和
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 10 10 10 分
【问题描述】
给定 n n n 个整数 a 1 , a 2 , ⋯ , a n a_1, a_2, \cdots , a_n a1,a2,⋯,an,求它们两两相乘再相加的和,即 S = a 1 ⋅ a 2 + a 1 ⋅ a 3 + ⋯ + a 1 ⋅ a n + a 2 ⋅ a 3 + ⋯ + a n − 2 ⋅ a n − 1 + a n − 2 ⋅ a n + a n − 1 ⋅ a n 。 S = a_1\cdot a_2 + a_1\cdot a_3 + \cdots + a_1\cdot a_n + a_2\cdot a_3 +\cdots + a_{n−2}\cdot a_{n−1} + a_{n−2}\cdot a_n + a_{n−1}\cdot a_n。 S=a1⋅a2+a1⋅a3+⋯+a1⋅an+a2⋅a3+⋯+an−2⋅an−1+an−2⋅an+an−1⋅an。
【输入格式】
输入的第一行包含一个整数 n n n 。
第二行包含 n n n 个整数 a 1 , a 2 , ⋯ , a n a_1, a_2,\cdots,a_n a1,a2,⋯,an。
【输出格式】
输出一个整数 S S S,表示所求的和。请使用合适的数据类型进行运算。
【样例输入】
4
1 3 6 9
【样例输出】
117
【评测用例规模与约定】
对于 30 % 30\% 30% 的数据, 1 ≤ n ≤ 1000 , 1 ≤ a i ≤ 100 1 ≤ n ≤ 1000,1 ≤ a_i ≤ 100 1≤n≤1000,1≤ai≤100。
对于所有评测用例, 1 ≤ n ≤ 200000 , 1 ≤ a i ≤ 1000 1 ≤ n ≤ 200000,1 ≤ a_i ≤ 1000 1≤n≤200000,1≤ai≤1000。
公式递推
将 S S S 中包含 a 1 a_1 a1 的项整理出来,有:
S = a 1 ⋅ ( a 2 + a 3 + ⋯ + a n ) + a 2 ⋅ a 3 + ⋯ + a n − 2 ⋅ a n − 1 + a n − 2 ⋅ a n + a n − 1 ⋅ a n S=a_1\cdot(a_2+a_3+\cdots+a_n)+ a_2\cdot a_3 +\cdots + a_{n−2}\cdot a_{n−1} + a_{n−2}\cdot a_n + a_{n−1}\cdot a_n S=a1⋅(a2+a3+⋯+an)+a2⋅a3+⋯+an−2⋅an−1+an−2⋅an+an−1⋅an
同样的将余项中包含 a 2 a_2 a2、 a 3 a_3 a3、 ⋯ \cdots ⋯、 a n a_n an 的项整理出来:
S = a 1 ⋅ ( a 2 + a 3 + ⋯ + a n ) + a 2 ⋅ ( a 3 + a 4 + ⋯ + a n ) + ⋯ + a n − 1 ⋅ a n = a 1 ⋅ ∑ i = 2 n a i + a 2 ⋅ ∑ i = 3 n a i + ⋯ + a n − 1 ⋅ ∑ i = n n a i \begin{aligned}S&=a_1\cdot(a_2+a_3+\cdots+a_n)+ a_2\cdot(a_3+a_4+\cdots+a_n)+\cdots+a_{n-1}\cdot a_n\\&=a_1\cdot\sum_{i=2}^na_i+a_2\cdot \sum_{i=3}^na_i+\cdots+a_{n-1}\cdot\sum_{i=n}^{n}a_i\end{aligned} S=a1⋅(a2+a3+⋯+an)+a2⋅(a3+a4+⋯+an)+⋯+an−1⋅an=a1⋅i=2∑nai+a2⋅i=3∑nai+⋯+an−1⋅i=n∑nai
也就 S S S 等于每个元素乘以右边所有元素的和的和,考虑到实现计算的代码量,我们将 S S S 的项重排,重新整理出:
S = a 1 ⋅ ∑ i = 1 0 a i + a 2 ⋅ ∑ i = 1 1 a i + ⋯ + a n ⋅ ∑ i = 1 n − 1 a i S=a_1\cdot\displaystyle\sum_{i=1}^{0}a_i+a_2\cdot \sum_{i=1}^{1}a_i+\cdots+a_{n}\cdot\sum_{i=1}^{n-1}a_i S=a1⋅i=1∑0ai+a2⋅i=1∑1ai+⋯+an⋅i=1∑n−1ai
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
void run() {
int n = nextInt(), sum = 0;
long a, ans = 0;
while(n-- > 0) {
a = nextInt();
ans += a * sum;
sum += a;
}
System.out.println(ans);
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
试题 D: GCD
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 10 10 10 分
【问题描述】
给定两个不同的正整数 a , b a, b a,b,求一个正整数 k k k 使得 gcd ( a + k , b + k ) \gcd(a + k, b + k) gcd(a+k,b+k) 尽可能大,其中 gcd ( a , b ) \gcd(a, b) gcd(a,b) 表示 a a a 和 b b b 的最大公约数,如果存在多个 k k k,请输出所有满足条件的 k k k 中最小的那个。
【输入格式】
输入一行包含两个正整数 a , b a, b a,b,用一个空格分隔。
【输出格式】
输出一行包含一个正整数 k k k。
【样例输入】
5 7
【样例输出】
1
【评测用例规模与约定】
对于 20 % 20\% 20% 的评测用例, a < b ≤ 1 0 5 a < b ≤ 10^5 a<b≤105;
对于 40 % 40\% 40% 的评测用例, a < b ≤ 1 0 9 a < b ≤ 10^9 a<b≤109;
对于所有评测用例, 1 ≤ a < b ≤ 1 0 18 1 ≤ a < b ≤ 10^{18} 1≤a<b≤1018。
更相减损术
更相减损术告诉我们,对于整数 a , b a,b a,b,若 a ≥ b a\geq b a≥b,都有 gcd ( a , b ) = gcd ( a − b , b ) = gcd ( a , a − b ) \gcd(a,b) = \gcd(a-b,b) = \gcd(a,a-b) gcd(a,b)=gcd(a−b,b)=gcd(a,a−b)。
将 k k k 代入到式中,我们的目标就是使 gcd ( a + k , a − b ) \gcd(a+k,a-b) gcd(a+k,a−b)、 gcd ( b + k , a − b ) \gcd(b+k,a-b) gcd(b+k,a−b) 最大。
显然最大为 ∣ a − b ∣ |a-b| ∣a−b∣,此时 k k k 取 min { − a , − b } ( m o d ∣ a − b ∣ ) \min\{-a,-b\} \pmod{|a-b|} min{−a,−b}(mod∣a−b∣) 最小。
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
public class Main {
public static void main(String[] args) { new Main().run(); }
void run() {
InputReader in = new InputReader(System.in);
long a = in.nextLong(), b = in.nextLong();
long c = abs(a - b);
if (c == 0 || c == 1) System.out.print("1");
else System.out.print(min((-a % c + c) % c, (-b % c + c) % c));
}
long min(long arg1, long arg2) { return arg1 < arg2 ? arg1 : arg2; }
long abs(long arg) { return arg > 0 ? arg : -arg; }
class InputReader {
BufferedReader reader;
StringTokenizer token;
InputReader(InputStream in) { this.reader = new BufferedReader(new InputStreamReader(in)); }
String next() {
if (token == null || !token.hasMoreTokens()) {
try {
token = new StringTokenizer(reader.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return token.nextToken();
}
long nextLong() { return Long.parseLong(next()); }
}
}
试题 E: 蜂巢
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 15 15 15 分
【问题描述】
蜂巢由大量的六边形拼接而成,定义蜂巢中的方向为 : : : 0 0 0 表示正西方向, 1 1 1 表示西偏北 60 60 60°, 2 2 2 表示东偏北 60 60 60°, 3 3 3 表示正东, 4 4 4 表示东偏南 60 60 60°, 5 5 5 表示西偏南 60 60 60°。
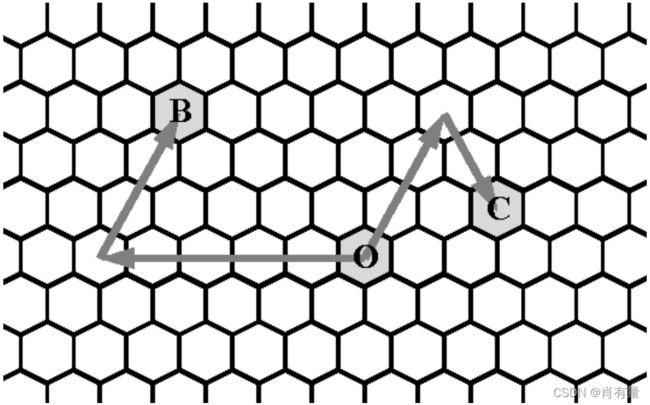
对于给定的一点 O O O,我们以 O O O 为原点定义坐标系,如果一个点 A A A 由 O O O 点先向 d d d 方向走 p p p 步再向 ( d + 2 ) m o d 6 (d + 2)\mod\: 6 (d+2)mod6 方向( d d d 的顺时针 120 120 120° 方向)走 q q q 步到达,则这个点的坐标定义为 ( d , p , q ) (d, p, q) (d,p,q)。在蜂窝中,一个点的坐标可能有多种。
下图给出了点 B ( 0 , 5 , 3 ) B(0, 5, 3) B(0,5,3) 和点 C ( 2 , 3 , 2 ) C(2, 3, 2) C(2,3,2) 的示意。
给定点 ( d 1 , p 1 , q 1 ) (d_1, p_1, q_1) (d1,p1,q1) 和点 ( d 2 , p 2 , q 2 ) (d_2, p_2, q_2) (d2,p2,q2),请问他们之间最少走多少步可以到达?
【输入格式】
输入一行包含 6 6 6 个整数 d 1 , p 1 , q 1 , d 2 , p 2 , q 2 d_1, p_1, q_1, d_2, p_2, q_2 d1,p1,q1,d2,p2,q2 表示两个点的坐标,相邻两个整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示两点之间最少走多少步可以到达。
【样例输入】
0 5 3 2 3 2
【样例输出】
7
【评测用例规模与约定】
对于 25 % 25\% 25% 的评测用例, p 1 , p 2 ≤ 1 0 3 p_1, p_2 ≤ 10^3 p1,p2≤103;
对于 50 % 50\% 50% 的评测用例, p 1 , p 2 ≤ 1 0 5 p_1, p_2 ≤ 10^5 p1,p2≤105;
对于 75 % 75\% 75% 的评测用例, p 1 , p 2 ≤ 1 0 7 p_1, p_2 ≤ 10^7 p1,p2≤107;
对于所有评测用例, 0 ≤ d 1 , d 2 ≤ 5 , 0 ≤ q 1 < p 1 ≤ 1 0 9 , 0 ≤ q 2 < p 2 ≤ 1 0 9 0 ≤ d_1, d_2 ≤ 5,0 ≤ q_1 < p_1 ≤ 10^9,0 ≤ q_2 < p_2 ≤ 10^9 0≤d1,d2≤5,0≤q1<p1≤109,0≤q2<p2≤109。
蜂巢中,两点之间的最短路与欧几里得度量无关,如下图所示 : : :
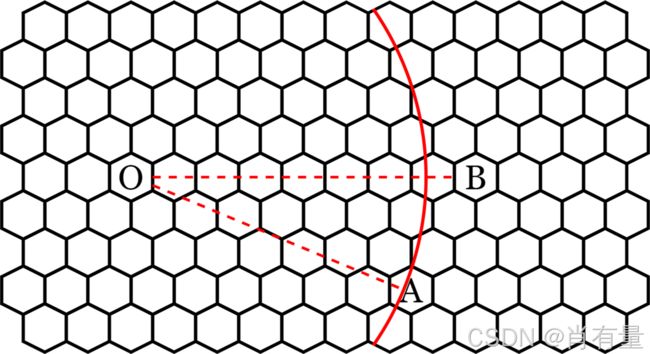
因此我们无法动用欧氏几何中的性质和公式进行计算,但我们可以围绕着原点进行 B F S \mathrm{BFS} BFS 观察一下蜂巢中最短路的性质,如图 : : :

图中颜色越浅的节点表示离原点越远,颜色相同的节点表示从原点出发到该些点的最短路步数均相同,容易发现,它们恰围成一个六边形,如点 A A A 处在从原点 0 0 0 出发向外扩散的第 i i i 层六边形之上,则表示 A A A 与 O O O 之间存在着一条步数为 i i i 的最短路, A A A 与这个六边形边上的节点到达 O O O 的最短路步数均相等。
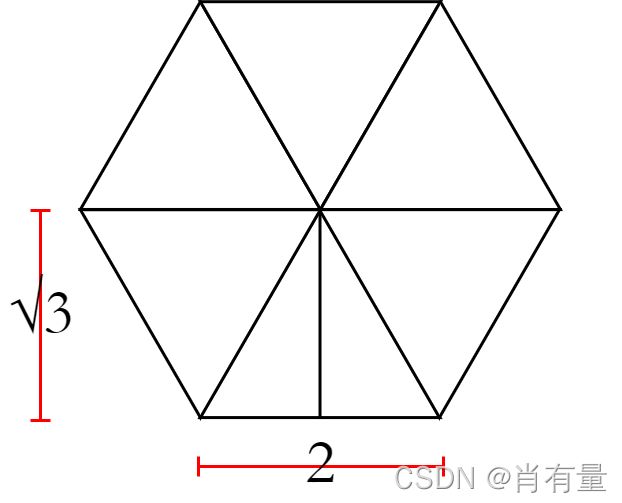
我们定义每个小六边形的中心点为它在平面直角坐标系上的坐标 ( x , y ) (x,y) (x,y),它的边长为 2 2 2,根据勾股定理,它的边心距为 3 \sqrt 3 3,对于题目给定的两点,我们先将其转换为 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)、 ( x 2 , y 2 ) (x_2,y_2) (x2,y2),然后将 ( x 2 , y 2 ) (x_2,y_2) (x2,y2) 变换为 ( x 2 + k , y 2 + 2 k 3 ) (x_2 +k,y_2+2k\sqrt 3) (x2+k,y2+2k3), y 1 = y 2 + 2 k 3 y1 = y_2+2k\sqrt 3 y1=y2+2k3,此时两点间的最短路步数显然为 ∣ x 1 − x 2 2 ∣ \left|\cfrac {x_1-x_2}2\right| ∣∣∣∣∣2x1−x2∣∣∣∣∣,并且按上述性质它与原命题等价,并且 y y y 并不直接参与运算,我们可以对所有的 y y y 除上一个 3 \sqrt 3 3 来保证精度问题。
对于题目给定的坐标到点我们也采用类似的方式转换为平面直角坐标系上坐标,
由于没有数据调试成本太高,所以这里只给出这个思路的基本实现,不保证程序的正确性。
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
int[][] offset = {{-2, 0}, {-1, 1}, {1, 1}, {2, 0}, {1, -1}, {-1, -1}};
void run() {
int d = nextInt();
long p = nextInt();
long q = nextInt();
long x1, y1, x2, y2;
x1 = (offset[d][0] + offset[(d + 2) % 6][0]) * p;
y1 = (offset[d][1] + offset[(d + 2) % 6][1]) * q;
d = nextInt(); p = nextInt(); q = nextInt();
x2 = (offset[d][0] + offset[(d + 2) % 6][0]) * p;
y2 = (offset[d][1] + offset[(d + 2) % 6][1]) * q;
long k = y2 - y1;
System.out.println((min(abs(x1 - k * x2), abs(x1 + k * x2)) + 1) / 2);
}
long min(long arg1, long arg2) { return arg1 < arg2 ? arg1 : arg2; }
long abs(long arg) { return arg > 0 ? arg : -arg; }
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
试题 F: 全排列的价值
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 15 15 15 分
【问题描述】
对于一个排列 A = ( a 1 , a 2 , ⋅ ⋅ ⋅ , a n ) A = (a_1, a_2, · · · , a_n) A=(a1,a2,⋅⋅⋅,an),定义价值 c i c_i ci 为 a 1 a_1 a1 至 a i − 1 a_{i−1} ai−1 中小于 a i a_i ai 的数的个数,即 c i = ∣ { a j ∣ j < i , a j < a i } ∣ c_i = |\{a_j | j < i, a_j < a_i\}| ci=∣{aj∣j<i,aj<ai}∣。定义 A A A 的价值为 ∑ i = 1 n c i \sum_{i=1}^n c_i ∑i=1nci。
给定 n n n,求 1 1 1 至 n n n 的全排列中所有排列的价值之和。
【输入格式】
输入一行包含一个整数 n n n。
【输出格式】
输出一行包含一个整数表示答案,由于所有排列的价值之和可能很大,请输出这个数除以 998244353 998244353 998244353 的余数。
【样例输入 1】
3
【样例输出 1】
9
【样例输入 2】
2022
【样例输出 2】
593300958
【样例说明】
1 1 1 至 3 3 3 构成的所有排列的价值如下 : : :
( 1 , 2 , 3 ) : 0 + 1 + 2 = 3 (1, 2, 3) : 0 + 1 + 2 = 3 (1,2,3):0+1+2=3;
( 1 , 3 , 2 ) : 0 + 1 + 1 = 2 (1, 3, 2) : 0 + 1 + 1 = 2 (1,3,2):0+1+1=2;
( 2 , 1 , 3 ) : 0 + 0 + 2 = 2 (2, 1, 3) : 0 + 0 + 2 = 2 (2,1,3):0+0+2=2;
( 2 , 3 , 1 ) : 0 + 1 + 0 = 1 (2, 3, 1) : 0 + 1 + 0 = 1 (2,3,1):0+1+0=1;
( 3 , 1 , 2 ) : 0 + 0 + 1 = 1 (3, 1, 2) : 0 + 0 + 1 = 1 (3,1,2):0+0+1=1;
( 3 , 2 , 1 ) : 0 + 0 + 0 = 0 (3, 2, 1) : 0 + 0 + 0 = 0 (3,2,1):0+0+0=0;
故总和为 3 + 2 + 2 + 1 + 1 = 9 3 + 2 + 2 + 1 + 1 = 9 3+2+2+1+1=9。
【评测用例规模与约定】
对于 40 % 40\% 40% 的评测用例, n ≤ 20 n ≤ 20 n≤20;
对于 70 % 70\% 70% 的评测用例, n ≤ 5000 n ≤ 5000 n≤5000;
对于所有评测用例, 2 ≤ n ≤ 1 0 6 2 ≤ n ≤ 10^6 2≤n≤106。
公式递推
考虑将价值按每个元素在不同排列中的贡献划分,以样例 1 1 1 为例 : : :
1 1 1 在任何排列中都没有贡献;
2 2 2 在 ( 1 , 2 , 3 ) 、 ( 1 , 3 , 2 ) 、 ( 3 , 1 , 2 ) (1, 2, 3)、(1, 3, 2)、(3, 1, 2) (1,2,3)、(1,3,2)、(3,1,2) 中的贡献均为 1 1 1;
3 3 3 在 ( 1 , 3 , 2 ) 、 ( 2 , 3 , 1 ) (1, 3, 2) 、(2, 3, 1) (1,3,2)、(2,3,1) 的贡献为 1 1 1;在 ( 1 , 2 , 3 ) 、 ( 2 , 1 , 3 ) (1, 2, 3) 、(2, 1, 3) (1,2,3)、(2,1,3) 的贡献为 2 2 2。
设 V a V_a Va 为 a a a 在所有排列中的贡献,则 a n s = ∑ a = 1 n V a \mathrm{ans}=\sum_{a=1}^nV_a ans=∑a=1nVa,而 a a a 能提供的贡献只能是 [ 1 , n ) [1,n) [1,n),考虑按贡献值进一步将 V a V_a Va 拆分为 ∑ i = 1 a − 1 i v a , i \sum_{i=1}^{a-1}iv_{a,i} ∑i=1a−1iva,i, v a , i v_{a,i} va,i 为 a a a 的贡献为 i i i 的排列个数,要使 a a a 的贡献为 i i i,可以将 i i i 个比 a a a 小的数放在 a a a 左侧,剩余 a − i − 1 a-i-1 a−i−1 放在 a a a 右侧,这样的组合个数有 ( a − i − 1 ) ! A a − 1 i (a-i-1)!A_{a-1}^i (a−i−1)!Aa−1i,然后将大于 a a a 的 n − a n-a n−a 个数任意的插入到这个组合中,最终 v a , i = ( a − i − 1 ) ! A a − 1 i A n n − a v_{a,i} = (a-i-1)!A_{a-1}^iA_n^{n-a} va,i=(a−i−1)!Aa−1iAnn−a,
整理可得 : : : a n s = ∑ a = 2 n ∑ i = 1 a − 1 i ( a − 1 ) ! n ! a ! = ∑ a = 2 n n ! a ∑ i = 1 a − 1 i \mathrm{ans}=\sum_{a=2}^n\sum_{i=1}^{a-1}i\frac{(a-1)!n!}{a!}=\sum_{a=2}^n\frac{n!}a\sum_{i=1}^{a-1}i ans=a=2∑ni=1∑a−1ia!(a−1)!n!=a=2∑nan!i=1∑a−1i
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
int p = 998244353, inv2 = 499122177;
void run() {
long ans = 0;
int n = nextInt();
long[] prod = new long[n + 1];
prod[0] = 1;
for (int i = 1; i <= n; ++i) prod[i] = prod[i - 1] * i % p;
for (int a = 2; a <= n; ++a) {
ans = (ans + prod[n] * qpow(a, p - 2) % p * a * (a - 1) % p * inv2) % p;
}
System.out.println(ans);
}
long qpow(long a, int b) {
long res = 1;
while (b > 0) {
if (b % 2 == 1) res = res * a % p;
a = a * a % p;
b /= 2;
}
return res;
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
好像中间推复杂了,
没上过高中,体谅一下。
试题 G: 青蛙过河
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 20 20 20 分
【问题描述】
小青蛙住在一条河边,它想到河对岸的学校去学习。小青蛙打算经过河里的石头跳到对岸。
河里的石头排成了一条直线,小青蛙每次跳跃必须落在一块石头或者岸上。不过,每块石头有一个高度,每次小青蛙从一块石头起跳,这块石头的高度就会下降 1 1 1,当石头的高度下降到 0 0 0 时小青蛙不能再跳到这块石头上 ( ( (某次跳跃后使石头高度下降到 0 0 0 是允许的 ) ) )。
小青蛙一共需要去学校上 x x x 天课,所以它需要往返 2 x 2x 2x 次。当小青蛙具有一个跳跃能力 y y y 时,它能跳不超过 y y y 的距离。
请问小青蛙的跳跃能力至少是多少才能用这些石头上完 x x x 次课。
【输入格式】
输入的第一行包含两个整数 n , x n, x n,x,分别表示河的宽度和小青蛙需要去学校的天数。请注意 2 x 2x 2x 才是实际过河的次数。
第二行包含 n − 1 n − 1 n−1 个非负整数 H 1 , H 2 , ⋯ , H n − 1 H_1, H_2,\cdots, H_{n−1} H1,H2,⋯,Hn−1,其中 H i > 0 H_i > 0 Hi>0 表示在河中与小青蛙的家相距 i i i 的地方有一块高度为 H i H_i Hi 的石头, H i = 0 H_i = 0 Hi=0 表示这个位置没有石头。
【输出格式】
输出一行,包含一个整数,表示小青蛙需要的最低跳跃能力。
【样例输入】
5 1
1 0 1 0
【样例输出】
4
【样例解释】
由于只有两块高度为 1 1 1 的石头,所以往返只能各用一块。第 1 1 1 块石头和对岸的距离为 4 4 4,如果小青蛙的跳跃能力为 3 3 3 则无法满足要求。所以小青蛙最少需要 4 4 4 的跳跃能力。
【评测用例规模与约定】
对于 30 % 30\% 30% 的评测用例, n ≤ 100 n ≤ 100 n≤100;
对于 60 % 60\% 60% 的评测用例, n ≤ 1000 n ≤ 1000 n≤1000;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 , 1 ≤ x ≤ 1 0 9 , 1 ≤ H i ≤ 1 0 4 1 ≤ n ≤ 10^5, 1 ≤ x ≤ 10^9, 1 ≤ H^i ≤ 10^4 1≤n≤105,1≤x≤109,1≤Hi≤104。
二分最大流
可以将转成最大流模型,然后二分答案。
但应付 1 0 5 10^5 105 的数据还是显得捉襟见肘,
摆了,不写了。
试题 H: 因数平方和
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 20 20 20 分
【问题描述】
记 f ( x ) f(x) f(x) 为 x x x 的所有因数的平方的和。例如 : f ( 12 ) = 1 2 + 2 2 + 3 2 + 4 2 + 6 2 + 1 2 2 :f(12) = 1^2 + 2^2 + 3^2 + 4^2 + 6^2 +12^2 :f(12)=12+22+32+42+62+122。
定义 g ( n ) = ∑ i = 1 n f ( i ) g(n) = \sum^n_{i=1}f(i) g(n)=∑i=1nf(i)。给定 n n n, 求 g ( n ) g(n) g(n) 除以 1 0 9 + 7 10^9 + 7 109+7 的余数。
【输入格式】
输入一行包含一个正整数 n n n。
【输出格式】
输出一个整数表示答案 g ( n ) g(n) g(n) 除以 1 0 9 + 7 10^9 + 7 109+7 的余数。
【样例输入】
100000
【样例输出】
680584257
【评测用例规模与约定】
对于 20 % 20\% 20% 的评测用例, n ≤ 1 0 5 n ≤ 10^5 n≤105。
对于 30 % 30\% 30% 的评测用例, n ≤ 1 0 7 n ≤ 10^7 n≤107。
对于所有评测用例, 1 ≤ n ≤ 1 0 9 1 ≤ n ≤ 10^9 1≤n≤109。
数论分块
根据倍数法求 [ 1 , n ] [1,n] [1,n] 中每个数的因数的完备性可得知:
[ 1 , n ] [1,n] [1,n] 中因数有 1 1 1 的数有 ⌊ n 1 ⌋ \lfloor\frac n1\rfloor ⌊1n⌋ 个;
[ 1 , n ] [1,n] [1,n] 中因数有 2 2 2 的数有 ⌊ n 2 ⌋ \lfloor\frac n2\rfloor ⌊2n⌋ 个;
⋯ ⋯ \cdots\cdots ⋯⋯
[ 1 , n ] [1,n] [1,n] 中因数有 n n n 的数有 ⌊ n n ⌋ \lfloor\frac nn\rfloor ⌊nn⌋ 个。
于是我们可以将和式 g ( n ) = ∑ i = 1 n f ( i ) g(n) = \sum^n_{i=1}f(i) g(n)=∑i=1nf(i) 演绎为
g ( n ) = ∑ i = 1 n ( ⌊ n i ⌋ i 2 ) = ∑ l ∣ l ∈ u n i q u e { ⌊ n i ⌋ ∣ i ∈ [ 1 , n ] } ( ⌊ n ⌊ n l ⌋ ⌋ − l + 1 ) ( l 2 + ( l + 1 ) 2 + ⋯ + ⌊ n ⌊ n l ⌋ ⌋ 2 ) \begin{aligned}g(n) &= \sum_{i=1}^n(\lfloor\frac ni\rfloor i^2)\\&=\sum_{l|l\in\mathrm{unique\{\lfloor\frac ni\rfloor|i\in[1,n]\}}}\left(\left\lfloor\dfrac{\ n\ }{\lfloor\frac nl\rfloor}\right\rfloor-l+1\right)(l^2+(l+1)^2+\cdots+\left\lfloor\frac{\ n\ }{\lfloor\frac nl\rfloor}\right\rfloor^2)\end{aligned} g(n)=i=1∑n(⌊in⌋i2)=l∣l∈unique{⌊in⌋∣i∈[1,n]}∑(⌊⌊ln⌋ n ⌋−l+1)(l2+(l+1)2+⋯+⌊⌊ln⌋ n ⌋2)
求解。
容易想到使用数论分块将和式计算的复杂度优化至 O ( n ) O(\sqrt n) O(n)。
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
int p = 1000000007, inv6 = 166666668;
void run() {
int n = nextInt();
long tmp, sum = 0, ans = 0;
for (int l = 1, r; l <= n; l = r + 1) {
r = n / (n / l);
tmp = sum;
sum = r * (r + 1L) % p * (2 * r + 1) % p * inv6 % p;
ans = (ans + (n / l) * (sum - tmp) + p) % p;
}
System.out.println(ans);
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
试题 I: 最优清零方案
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 25 25 25 分
【问题描述】
给定一个长度为 N N N 的数列 A 1 , A 2 , ⋯ , A N A_1, A_2,\cdots, A_N A1,A2,⋯,AN。现在小蓝想通过若干次操作将这个数列中每个数字清零。
每次操作小蓝可以选择以下两种之一 : : :
1. 1. 1. 选择一个大于 0 0 0 的整数,将它减去 1 1 1;
2. 2. 2. 选择连续 K K K 个大于 0 0 0 的整数,将它们各减去 1 1 1。
小蓝最少经过几次操作可以将整个数列清零?
【输入格式】
输入第一行包含两个整数 N N N 和 K K K。
第二行包含 N N N 个整数 A 1 , A 2 , ⋯ , A N A_1, A_2,\cdots, A_N A1,A2,⋯,AN。
【输出格式】
输出一个整数表示答案。
【样例输入】
4 2
1 2 3 4
【样例输出】
6
【评测用例规模与约定】
对于 20 % 20\% 20% 的评测用例, 1 ≤ K ≤ N ≤ 10 1 ≤ K ≤ N ≤ 10 1≤K≤N≤10;
对于 40 % 40\% 40% 的评测用例, 1 ≤ K ≤ N ≤ 100 1 ≤ K ≤ N ≤ 100 1≤K≤N≤100;
对于 50 % 50\% 50% 的评测用例, 1 ≤ K ≤ N ≤ 1000 1 ≤ K ≤ N ≤ 1000 1≤K≤N≤1000;
对于 60 % 60\% 60% 的评测用例, 1 ≤ K ≤ N ≤ 10000 1 ≤ K ≤ N ≤ 10000 1≤K≤N≤10000;
对于 70 % 70\% 70% 的评测用例, 1 ≤ K ≤ N ≤ 100000 1 ≤ K ≤ N ≤ 100000 1≤K≤N≤100000;
对于所有评测用例, 1 ≤ K ≤ N ≤ 1000000 , 1 ≤ A i ≤ 1000000 1 ≤ K ≤ N ≤ 1000000,1 ≤ A_i ≤ 1000000 1≤K≤N≤1000000,1≤Ai≤1000000。
\\ 应该也是贪心,证明太麻烦了,摆
试题 J: 推导部分和
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 25 25 25 分
【问题描述】
对于一个长度为 N N N 的整数数列 A 1 , A 2 , ⋯ , A N A_1, A_2,\cdots,A_N A1,A2,⋯,AN,小蓝想知道下标 l l l 到 r r r 的部分和 ∑ i = l r = A l + A l + 1 + ⋯ + A r \sum_{i=l}^r= A_l + A_{l+1} +\cdots+ A_r ∑i=lr=Al+Al+1+⋯+Ar 是多少?
然而,小蓝并不知道数列中每个数的值是多少,他只知道它的 M M M 个部分和的值。其中第 i i i 个部分和是下标 l i l_i li 到 r i r_i ri 的部分和 ∑ j = l i r i = A l i + A l i + 1 + ⋯ + A r i \sum_{j=l_i}^{r_i}= A_{l_i} + A_{l_i+1} +\cdots+ A_{r_i} ∑j=liri=Ali+Ali+1+⋯+Ari 值是 S i S_i Si。
【输入格式】
第一行包含 3 3 3 个整数 N 、 M N、M N、M 和 Q Q Q。分别代表数组长度、已知的部分和数量和询问的部分和数量。
接下来 M M M 行,每行包含 3 3 3 个整数 l i , r i , S i l_i, r_i, S_i li,ri,Si。
接下来 Q Q Q 行,每行包含 2 2 2 个整数 l l l 和 r r r,代表一个小蓝想知道的部分和。
【输出格式】
对于每个询问,输出一行包含一个整数表示答案。如果答案无法确定,输出 U N K N O W N \mathrm{UNKNOWN} UNKNOWN。
【样例输入】
5 3 3
1 5 15
4 5 9
2 3 5
1 5
1 3
1 2
【样例输出】
15
6
UNKNOWN
【评测用例规模与约定】
对于 10 % 10\% 10% 的评测用例, 1 ≤ N , M , Q ≤ 10 , − 100 ≤ S i ≤ 100 1 ≤ N, M, Q ≤ 10,−100 ≤ S_i ≤ 100 1≤N,M,Q≤10,−100≤Si≤100。
对于 20 % 20\% 20% 的评测用例, 1 ≤ N , M , Q ≤ 20 , − 1000 ≤ S i ≤ 1000 1 ≤ N, M, Q ≤ 20,−1000 ≤ S_i ≤ 1000 1≤N,M,Q≤20,−1000≤Si≤1000。
对于 30 % 30\% 30% 的评测用例, 1 ≤ N , M , Q ≤ 50 , − 10000 ≤ S i ≤ 10000 1 ≤ N, M, Q ≤ 50,−10000 ≤ S_i ≤ 10000 1≤N,M,Q≤50,−10000≤Si≤10000。
对于 40 % 40\% 40% 的评测用例, 1 ≤ N , M , Q ≤ 1000 , − 1 0 6 ≤ S i ≤ 1 0 6 1 ≤ N, M, Q ≤ 1000,−10^6 ≤ S_i ≤ 10^6 1≤N,M,Q≤1000,−106≤Si≤106。
对于 60 % 60\% 60% 的评测用例, 1 ≤ N , M , Q ≤ 10000 , − 1 0 9 ≤ S i ≤ 1 0 9 1 ≤ N, M, Q ≤ 10000,−10^9 ≤ S_i ≤ 10^9 1≤N,M,Q≤10000,−109≤Si≤109。
对于所有评测用例, 1 ≤ N , M , Q ≤ 1 0 5 , − 1 0 12 ≤ S i ≤ 1 0 12 , 1 ≤ l i ≤ r i ≤ N , 1 ≤ l ≤ r ≤ N 1 ≤ N, M, Q ≤ 10^5,−10^{12} ≤ S_i ≤ 10^{12},1 ≤ l_i ≤ r_i ≤ N,1 ≤ l ≤ r ≤ N 1≤N,M,Q≤105,−1012≤Si≤1012,1≤li≤ri≤N,1≤l≤r≤N。数据保证没有矛盾。
树模型
对于每一组 ( l i , r i , S i ) (l_i,r_i,S_i) (li,ri,Si),我们是否能找到一种表示方法,将相关联的区间和用更一般的方式表示出来,显然这是可以的。
对于每一组 ( l i , r i , S i ) (l_i,r_i,S_i) (li,ri,Si),我们将其视为 l i − 1 ⟶ S i r i l_i-1\stackrel{S_i}{\longrightarrow} r_i li−1⟶Siri、 r i ⟶ − S i l i − 1 r_i\stackrel{-S_i}{\longrightarrow} l_i-1 ri⟶−Sili−1 上的有向边,一开始我们维护一个空图,读取完全部部分和后它可能会形成一片森林,对于每一个根节点 l r t l_{rt} lrt,我们做一遍深度优先遍历,下传边权同时对它的子树染色,最后每一个子节点 r s o n r_{son} rson,都维护着 ∑ i = l r t + 1 r s o n \sum_{i=l_{rt}+1}^{r_{son}} ∑i=lrt+1rson 的信息,对于每一个查询 l , r l,r l,r,若 l − 1 l-1 l−1和 r r r 颜色相同,则 r r r 节点维护的信息减去 l − 1 l-1 l−1 所维护的信息,即是这段区间和,否则无法确定这段区间和。
整个过程可以视作不断的在做部分和的部分和,正确性是显然的,主要我不会证。
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.PrintWriter;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
void run() {
PrintWriter out = new PrintWriter(System.out);
int n = nextInt(), m = nextInt(), q = nextInt();
next = new int[m + 2 << 1];
val = new long[m + 2 << 1];
ver = new int[m + 2 << 1];
linked = new int[n + 1];
color = new int[n + 1];
sum = new long[n + 1];
while (m-- > 0)
add(nextInt() - 1, nextInt(), nextLong());
for (int i = 0; i <= n; ++i) dfs(i, ++cur);
while (q-- > 0) {
int l = nextInt() - 1;
int r = nextInt();
if (color[l] == color[r])
out.println(sum[r] - sum[l]);
else
out.println("UNKNOWN");
}
out.flush();
}
void dfs(int root, int c) {
if (color[root] > 0) return;
color[root] = c;
for (int i = linked[root]; i != 0; i = next[i]) {
sum[ver[i]] = sum[root] + val[i];
dfs(ver[i], c);
}
}
void add(int u, int v, long w) {
next[++cur] = linked[u]; linked[u] = cur; ver[cur] = v; val[cur] = w;
next[++cur] = linked[v]; linked[v] = cur; ver[cur] = u; val[cur] = -w;
}
int[] linked, color, next, ver;
long[] val, sum;
int cur;
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
long nextLong() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (long)in.nval;
}
}