哈里斯鹰优化算法(HHO)附matlab code链接
哈里斯鹰优化算法
- 算法简介
- 算法的实现过程
-
- 1. 探索阶段
- 2.探索到开发的转换
- 3.开发阶段
-
- 3.1软围攻
- 3.2硬围攻
- 3.3渐进式快速俯冲的软包围
- 3.4渐进式快速俯冲的硬包围
- 算法示意图
群智能算法学习笔记
笔记内容和仿真代码可能会不断改动
如有不当之处,欢迎指正
算法简介
哈里斯鹰优算法是化(Harris Hawks Optimization,HHO)是Heidari等于2019年提出的一种群体优化算法,该算法模拟哈里斯鹰(美国亚利桑那州南部的猛禽)的捕食行为,主要分为探索阶段、探索与开发转换阶段和开发阶段。
算法的实现过程
1. 探索阶段
哈里斯鹰会利用眼睛追踪和发现猎物,但有时候也会看不到猎物。因此,哈里斯鹰会花费几个小时去等待、观察和监视沙漠地带。在HHO中,哈里斯鹰是候选方案,每一过程中最佳的候选方案被视为是预期的猎物或接近预期的猎物。哈里斯鹰随机栖息在某些位置,并等待根据两种策略探测猎物。如果每种栖息策略的机会q均等,则当q<0.5时,哈里斯鹰会根据其它成员和猎物的位置进行栖息;当q>0.5时,哈里斯鹰会随机栖息在鹰群活动范围内的大树上,具体模型为,![]()
其中, X ( t + 1 ) X(t+1) X(t+1)是下一次迭代过程中鹰的位置向量, X r a b b i t ( t ) X_{rabbit}(t) Xrabbit(t)是猎物的位置(即拥有最优适应度的个体位置), X ( t ) X(t) X(t)是当前鹰的位置向量, r 1 r_1 r1、 r 2 r_2 r2、 r 3 r_3 r3、 r 4 r_4 r4和q是(0,1)中的随机数,LB、UB是是变量的的下限和上限, X r a n d X_rand Xrand是当前种群中随机选择的鹰的位置, X m ( t ) X_m(t) Xm(t)为个体平均位置。
![]()
2.探索到开发的转换
HHO算法可以从探索转移到开发,然后根据猎物的逃逸能量在不同的开发行为之间进行转换。在猎物的逃避过程中,能量将大大降低。猎物的逃逸能量为:
![]()
其中E表示猎物逃逸的能量,T是最大迭代次数, E 0 E_0 E0是其能量的初始状态。在HHO的迭代过程中 E 0 E_0 E0在(-1,1)内随机变化。当 E 0 E_0 E0的值从0减小到-1时,兔子物理标记,而当E0的值从0增大到1时,猎物的活动正在增强。动态逃逸能量E在迭代过程中呈下降趋势。当逃逸能量|E|≥1时,小鹰搜索不同的区域以探索猎物的位置,因此,HHO执行探索阶段;当|E| <1,算法尝试开发 探索阶段时解的邻域。总之,|E|≥1进行探索,|E| <1进行开发。
3.开发阶段
在此阶段中,哈里斯鹰对前一阶段中发现的预定猎物进行突袭。但是,猎物经常试图逃脱危险。因此,在实际情况下会出现不同的追逐风格。根据猎物的逃逸行为和哈里斯鹰的追逐策略,在HHO中提出了四种可能的策略来模拟攻击阶段。
猎物总是试图从危险中逃脱。假设r是猎物在突袭前逃脱的机会,成功逃脱(r <0.5)或未成功逃脱(r≥0.5)。不论猎物做什么,鹰都会以强硬或轻柔的围攻来捕获猎物。这意味着它们将根据猎物的保留能量从不同方向轻柔地或强硬地包围猎物。在实际情况下,鹰会越来越接近预期的猎物,并通过执行突袭而增加了合作杀死猎物的机会。几分钟后,逃逸的猎物将损失越来越多的能量;然后,鹰加强围攻过程,从而毫不费力地抓住疲惫的猎物。为了对该策略进行建模,并使HHO能够在软、硬围攻过程之间切换,使用了E参数。当**|E| ≥0.5时,进行软围攻**;当**|E| <0.5时,进行应围攻**。
3.1软围攻
当r≥0.5且|E|时≥0.5时,兔子仍然有足够的能量,尝试通过一些随机的误导性跳跃逃脱。在这些尝试中,哈里斯的鹰轻柔地包围它,使兔子更加疲惫,然后进行突击突袭。此行为通过以下规则建模:

其中 Δ X ( t ) \varDelta X(t) ΔX(t)为最优个体和当前个体的差值, r 5 r_5 r5 为0 到1 内的随机数, J 为兔子逃跑过程中的跳跃距离。
![]()
3.2硬围攻
当r≥0.5且|E|<0.5时,猎物非常疲惫,逃逸能量低。猎物既没有足够的能量摆脱,也没有逃脱的机会。因此哈里斯鹰使用硬包围的方式进行狩猎,公式如下:
![]()
3.3渐进式快速俯冲的软包围
当r<0.5且|E|>0.5时,猎物有机会从包围圈中逃脱,且逃逸能量足够,因此哈里斯鹰需要在进攻前形成一个更加智能的软包围圈,通过以下两个策略实施。当第一个策略无效时,执行第二个策略。
第一个策略更新公式:
![]()
第二个策略更新公式:
![]()
其中 D 为问题维度,S 是一个D 维的随机向量, LF 为Levy 飞行函数,公式如下:

其中 l l l 和 m m m 为0 到1 内均匀分布的随机数, β \beta β是取值为1.5
的常数。因此该阶段更新策略最终如下:
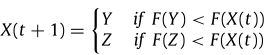
3.4渐进式快速俯冲的硬包围
当r<0.5且|E|<0.5时时,猎物有机会逃逸,但逃逸能量不足,因此哈里斯鹰在突袭前形成一个硬包围圈,缩小它们和猎物的平均距离,采用以下策略进行狩猎:

算法示意图

[1]: Heidari A A, Mirjalili S, Faris H, et al. Harris hawks optimization: Algorithm and applications[J]. Future Generation Computer Systems. 2019, 97: 849-872.
[2]: 汤安迪,韩统,徐登武,等. 混沌精英哈里斯鹰优化算法[J]. 计算机应用. 2021: 1-10.
matlab仿真代码下载链接
CSDN下载链接
原文下载链接