论文阅读Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift

Ar Xiv：1502.03167v3[cs。 LG]2015年3月2日

全文翻译

批量标准化：通过减少内部协方差移位来加速深度网络训练

Sergey Ioffe Google Inc., [email protected]
Christian Szegedy Google Inc., [email protected]
摘要
训练深度神经网络是复杂的，因为每个层的输入分布在训练过程中会随着前一层的参数变化而变化。 这通过要求较低的学习速率和仔细的参数初始化来减缓训练速度，并使训练具有饱和非线性的模型变得众所周知的困难。 我们将这种现象称为内部协变量移位，并通过归一化层输入来解决这个问题。我们的方法从使规范化成为模型体系结构的一部分和为每个训练小批执行规范化中汲取其力量。 批归一化允许我们使用更高的学习速率，并且对初始化不那么小心。 在某些情况下，它还起到了规范的作用，消除了信息漏失。 应用于最先进的图像分类模型，批量归一化实现了相同的精度，减少了14倍的训练步骤，并大大超过了原始模型。 利用批归一化网络的集合，我们改进了图像网分类的最佳发布结果：达到4.9%的前5验证误差（和4.8%的测试误差），超过了人类评分者的精度。
1. 引言
深度学习在视觉、言语和许多其他领域显著地促进了艺术的发展。 随机梯度下降(SGD)已被证明是训练深层网络的一种有效方法，而动量(Sutskever等人，2013年)和Adagrad(Duchi等人，2011年)等SGD变体已被用于实现最先进的性能。 对网络的参数Θ进行SGD优化，使损耗最小

其中x1…N是训练数据集。 使用SGD，训练分步骤进行，在每一步，我们考虑一个尺寸为m的小舱口x1.m。通过计算，小批被用来损失函数相对于参数的梯度。

使用小样本的例子，而不是一次一个例子，在几个方面是有帮助的。 首先，小批损失的梯度是训练集上梯度的估计，随着批处理大小的增加，训练集的质量提高。 其次，由于现代计算平台提供的并行性，批处理上的计算可以比单个示例的m计算更有效。
虽然随机梯度简单有效，但需要仔细调整模型超参数，特别是优化中使用的学习速率，以及模型参数的初始值。 训练是复杂的，因为每个层的输入都受到前面所有层的参数的影响-因此，随着网络的深入，网络参数的微小变化会放大。
层输入分布的变化提出了一个问题，因为层需要不断地适应新的分布。 当学习系统的输入分布发生变化时，据说会经历协变量转移(Shimodaira，2000)。 这通常是通过域适应来处理的(Jiang，2008)。 然而，协变量转移的概念可以扩展到整个学习系统之外，应用于其部分，如子网络或层。 考虑一个网络计算

其中F1和F2是任意变换，参数Θ1，Θ2要学习，以尽量减少损失ℓ。 学习Θ2可以看作是输入x=F1(u，Θ1)被输入到子网络中

例如，梯度下降步骤

(对于批处理大小m和学习速率α)与具有输入x的独立网络F2完全等价。 因此，使训练更有效的输入分布特性-例如在训练和测试数据之间具有相同的分布-也适用于训练子网络。 因此，随着时间的推移，x的分布保持固定是有利的。那么，Θ2也不必重新调整以补偿x分布的变化。
向子网络固定分配输入也会对子网络之外的层产生积极影响。考虑具有s型激活函数的层 其中u是层输入，权重矩阵W和偏置向量b是要学习的层参数， 随着|x|的增加，g‘(X)趋于零。 这意味着对于所有维度 除了绝对值较小的梯度外，流向u的梯度将消失，模型将缓慢训练。然而，由于x受W、b和下面所有层的参数的影响，训练过程中对这些参数的变化可能会将x的多个维度移动到非线性的饱和状态，并减缓收敛速度。这种效应随着网络深度的增加而放大。 在实践中，饱和问题和由此产生的消失梯度通常是通过使用校正线性单元来解决的(Nair & Hinton, 2010) 仔细初始化(Bengio & Glorot, 2010; Saxe et al., 2013) 和小的学习率。 然而，如果我们能够确保非线性输入的分布随着网络的训练而保持更稳定，那么优化器就不太可能陷入饱和状态，训练就会加速。
我们将深度网络内部节点分布的变化称为内部协方差移位。 消除它提供了更快培训的希望。 我们提出了一种新的机制，我们称之为批归一化，它朝着减少内部协变量转移迈出了一步，并在这样做的过程中显着地加速了深度神经网络的训练。它通过一个规范化步骤来完成这一点，该步骤修复了层输入的均值和方差。 批归一化也对通过网络的梯度流有有益的影响，通过减少梯度对参数或其初始值的尺度的依赖。 这使我们能够使用更高的学习率，而不存在发散的风险。 此外，批处理规范化了模型，减少了对数据消失的需求(Srivastava et al., 2014) 最后，批量归一化使使用饱和非线性成为可能，防止网络陷入饱和模式。在证券交易委员会。 在4.2我们将批处理规范化应用于性能最好的Image Net分类网络，并表明我们只能使用7%的训练步骤来匹配它的性能，并且可以进一步大大超过它的准确性。 通过对这些网络进行批量标准化训练的集成，我们实现了前5名的错误率，从而提高了图像网分类的最佳已知结果。
2减少内部协方差移
我们将内部协方差移位定义为由于训练过程中网络参数的变化而导致的网络激活分布的变化。 为了改进训练，我们寻求减少内部协变量转移。 通过固定层输入x的分布随着训练的进行，我们期望提高训练速度。 早已为人所知(LeCun et al., 1998b; Wiesler & Ney, 2011) 如果网络训练的输入被白化，则网络训练收敛得更快-即线性变换为零均值和单位方差，并且与装饰相关。 由于每一层都观察到下面各层产生的输入，因此对每一层的输入实现相同的白化是有利的。 通过将输入白化到每个层，我们将采取一步来实现输入的固定分布，这将消除内部协变量移位的不良影响。我们可以考虑在每个训练步骤或在某个区间进行白化激活，要么直接修改网络，要么改变优化算法的参数以依赖于网络激活值(Wiesler et al., 2014; Raiko et al., 2012; Povey et al., 2014; Desjardins & Kavukcuoglu). 然而，如果这些修改穿插在优化步骤中，那么梯度下降步骤可能会尝试以需要更新规范化的方式更新参数，从而降低梯度步骤的效果。 例如，考虑一个带有输入u的层，该层添加学习的偏置b，并通过减去在训练数据上计算的激活的平均值来将结果规范化：
当
是在训练集上x值的集合

如果梯度下降步骤忽略了E[x] 在b上的依赖，那么它会更新
当
那么

因此，更新到b的组合和随后的归一化变化导致层的输出没有变化，因此也没有损失。 随着训练的继续，b将无限期增长，而损失保持不变。 如果归一化不仅集中在中心，而且还扩展激活，这个问题就会变得更糟。 我们在初始实验中观察到了这一点，当归一化参数在梯度下降步骤之外计算时，模型就会爆炸。
上述方法的问题是，梯度下降优化没有考虑到规范化发生的事实。 为了解决这个问题，我们希望确保，对于任何参数值，网络总是产生具有所需分布的激活。 这样做将允许损失相对于模型参数的梯度来考虑归一化，以及它对模型参数Θ的依赖。再让x是一个层输入，作为一个2向量，X是训练数据集上这些输入的集合。 然后，规范化可以写成转换 这不仅取决于给定的训练示例x，而且取决于所有示例X-每个示例都取决于Θ是否由另一层生成x。 为了反向传播，我们需要计算雅可比行列式

忽略后一项将导致上述爆炸。 在这个框架内，白化层输入是昂贵的，因为它需要计算协方差矩阵Cov[x]=Ex∈X[xxT]]E[x]E[x]T及其逆平方根，以产生白化激活Cov[x]1/2(xÆE[x])，以及这些变换的导数进行反向传播。 这促使我们寻求一种替代方案，以一种可微的方式执行输入归一化，并且不需要在每次参数更新后对整个训练集进行分析。以前的一些方法(e.g. (Lyu & Simoncelli, 2008)) 使用在单个训练示例上计算的统计数据，或者在图像网络的情况下，在给定位置上使用不同的特征映射。 然而，这通过丢弃激活的绝对规模来改变网络的表示能力。我们希望通过规范训练示例中相对于整个训练数据统计的激活来保存网络中的信息。
3.归一化通过小批次统计
由于每个层的输入的完全白化是昂贵的，并且不是到处都是可微的，所以我们做了两个必要的简化。 首先，我们将不将层输入和输出中的特征联合白化，而是通过使每个标量特征具有零的均值和1的方差来独立地归一化。 对于具有d维输入x=(x（1）.x(d))的层，我们将对每个维度进行规范化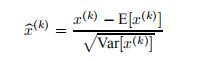
其中期望和方差是在训练数据集上计算的。 如(LeCun et al., 1998b) 这种规范化加速了收敛，即使在特征不相关的情况下也是如此。请注意，简单地规范一个层的每个输入可能会改变该层可以表示的内容。 例如，规范乙状结肠的输入将限制它们到非线性的线性状态。 为了解决这个问题，我们确保插入到网络中的转换能够表示身份转换。为了实现这个目标，对于每个激活x(K)，我们引入了一对参数γ(K)、β(K)，它们缩放和移动归一化值：
这些参数与原始模型参数一起学习，并恢复网络的表示能力。 事实上，通过设置γ(K)=pVar[x(K)]和β(K)=E[x(K)]，我们可以恢复原始激活，如果这是最佳的做法。在批处理设置中，每个训练步骤都基于整个训练集，我们将使用整个集合来规范激活。 然而，当使用随机优化时，这是不切实际的。 因此，我们进行了第二次简化：由于我们在随机梯度训练中使用了小批次，所以每个小批次的均值和方差都会产生每个激活的估计值。 这样，用于规范化的统计就可以完全参与梯度反向传播。请注意，使用小批次是通过计算每维方差而不是联合协方差来实现的；在联合情况下，需要正则化，因为小批次大小可能小于被白化的激活数，从而产生奇异协方差矩阵。考虑一个大小为m的小批B。由于规范化是独立地应用于每个激活，让我们专注于特定的激活x(K)，并省略k以获得清晰性。 我们在小批量中有这个激活的m值，
设归一化值为bx1.m，它们的线性变换为y1.m。我们指的是变换
作为批归一化变换。 我们提出了算法1中的BN变换。 在算法中，o是一个常数添加到小批方差中，以获得数值稳定性

算法1：批量归一化变换，应用于小批上的激活x。可以将BN变换添加到网络中以操作任何激活。在符号y=BNγ中，β(x)，我们相反，BNγ，β(X)既取决于培训示例，也取决于小批中的其他示例。 缩放和移位的值y被传递给其他网络层。 归一化激活bx是我们转换的内部，但它们的存在是至关重要的。指出，γ和β的参数是要学习的，但应该注意的是，BN变换并不独立地处理每个训练示例中的激活。相反，BNγ，β(X)既取决于培训示例，也取决于小批中的其他示例。 缩放和移位的值y被传递给其他网络层。 归一化激活bx是我们转换的内部，但它们的存在是至关重要的。任何bx的值的分布都有0的期望值和1的方差，只要每个小批的元素从相同的分布中采样，如果我们忽略o。 通过观察可以看出这一点
和
接受期望。 每个归一化激活bx(K)可以看作是由线性变换组成的子网络的输入
然后是由原始网络完成的其他处理。 这些子网络输入都有固定的均值和方差，尽管这些归一化的联合分布 在训练过程中可以改变，我们期望引入归一化输入可以加速子网络的训练，从而加速整个网络的训练。在训练过程中，我们需要通过这种变换反向传播损失ℓ的梯度，以及计算BN变换参数的梯度。 我们使用链式规则，如下（简化前）

因此，BN变换是将归一化激活引入网络的一种可微变换。 这确保了当模型是训练时，层可以继续学习内部协变量移动较少的输入分布，从而加速训练。 此外，应用于这些归一化激活的学习仿射变换允许BN变换表示身份变换并保持网络容量
3.1使用批量标准化网络进行培训和推理
根据Alg的说法，为了批处理-规范化网络，我们指定了一个激活子集，并为每个激活子集插入BN变换。 1. 以前接收x作为输入的任何层，现在接收BN(X)。使用批归一化的模型可以使用批处理梯度下降或随机梯度下降来训练，其小批尺寸m>1，或其任何变体，如Adagrad(Duchi et al., 2011). 依赖于小批量的激活的归一化允许有效的训练，但在推理过程中既不必要也不可取；我们希望输出只依赖于输入，确定性。 为此，一旦网络被训练，我们就使用规范化
使用人口，而不是小批量，统计。 忽略o，这些归一化激活具有与训练期间相同的均值0和方差1。我们使用无偏方差估计

其中期望超过训练大小m的小批次，σ2B是它们的样本差异。 使用移动平均线代替，我们可以跟踪模型的准确性，因为它训练。 由于均值和方差在推理过程中是固定的，归一化只是应用于每个激活的线性变换。 它可以进一步由γ的缩放和β的移位组成，以产生一个单一的线性变换，取代BN(X)。 算法2总结了训练批归一化网络的过程。

算法2：训练一个批量归一化网络
3.2批量归一化卷积网络
批归一化可以应用于网络中的任何一组激活。在这里，我们重点讨论由仿射变换和元素非线性组成的变换：
其中W和b是模型的学习参数，G（·）是s型或ReLU等非线性。这种公式包括完全连接层和卷积层。 我们在非线性之前立即添加BN变换，通过归一化x=Wu+b。 我们也可以归一化层输入u，但由于u很可能是另一个非线性的输出，它的分布形状很可能在训练过程中发生变化，限制它的第一和第二矩不会消除协变量位移。 相反，Wu+b更有可能具有对称的、非稀疏的分布，即“more Gaussian”(Hyv¨arinen & Oja, 2000) 归一化它很可能产生具有稳定分布的激活。请注意，由于我们规范了Wu+b，所以偏置b可以忽略，因为它的效果将被随后的平均减法取消(偏置的作用被Alg中的β所包含。 1)。 因此，z=g(Wu+b)被替换为
其中BN变换独立地应用于x=Wu的每个维数，每个维数有一对单独的学习参数γ(K)、β(K)。
对于卷积层，我们还希望归一化服从卷积性质-以便同一特征映射的不同元素在不同的位置以相同的方式归一化。 为了实现这一点，我们在一个小型舱内，在所有地点联合规范所有激活。 在阿尔格。 我们让B是一个特征映射中跨越小批和空间位置的元素的所有值的集合-因此对于一个小批大小m和大小p×q的特征映射，我们使用有效的小批大小 。 我们每个特征映射学习一对参数γ(k)和β(k)，而不是每个激活。 Alg。 对2进行类似的修改，以便在推理过程中，BN变换对给定特征映射中的每个激活应用相同的线性变换。
3.3批量标准化可以提高学习率
在传统的深度网络中，过高的学习速率可能导致梯度爆炸或消失，以及陷入较差的局部极小值。 批归一化有助于解决这些问题。 通过规范整个网络的激活，它防止参数的微小变化放大到梯度激活的更大和次优变化；例如，它防止训练陷入非线性的饱和状态。批量标准化也使训练对参数规模更有弹性。 通常，较大的学习速率可能会增加层参数的规模，从而放大反向传播过程中的梯度，导致模型爆炸。 然而，在批处理归一化的情况下，通过层的反向传播不受其参数规模的影响。 实际上，对于标量a，
我们可以证明这一点
尺度不影响雅可比层，也不影响梯度传播。 此外，较大的权重导致较小的梯度，批归一化将稳定参数的增长。我们进一步推测，批归一化可能导致层雅可比具有接近1的奇异值，这已知有利于训练(Saxe et al., 2013). 考虑两个具有归一化输入的连续层，以及这些归一化向量之间的转换 如果我们假设x和z是高斯和不相关的，对于给定的模型参数，F( x)≈Jx是一个线性变换，则Bx和Bz都具有单位协方差，
因此
因此，J的所有奇异值都等于1，这保留了反向传播过程中的梯度幅度。 在现实中，变换不是线性的，归一化值不能保证是高斯的，也不能独立的，但我们仍然期望批归一化有助于使梯度传播更好地表现出来。 批归一化对梯度传播的精确影响仍是一个有待进一步研究的领域
3.4批量标准化使模型正规化
当使用批归一化进行训练时，将结合小批中的其他示例看到一个训练示例，并且训练网络不再为给定的训练示例生成确定性值。 在我们的实验中，我们发现这种效应有利于网络的泛化。当Whereas Dropout (Srivastava et al., 2014) 通常用于减少过拟合，在批处理归一化网络中，我们发现它可以被移除或降低强度。
4实验
4.1随着时间推移的激活
为了验证内部协变量移位对训练的影响，以及批归一化对抗它的能力，我们考虑了在MNIST数据集上预测数字类的问题(LeCun et al., 1998a). 我们使用了一个非常简单的网络，以28x28二进制图像作为输入

图1：(A)使用和不使用批归一化训练的MNIST网络的测试精度与训练步骤的数量。 批量归一化有助于网络训练更快，达到更高的精度。 (b，c)输入分布在训练过程中演变成典型s型，显示为{15、50、85}百分位数。 批归一化使分布更加稳定，减少内部协变量移位。3个完全连接的隐藏层，每个层有100个激活。 每个隐层计算具有乙状结肠非线性的y=g(Wub)，权值W初始化为小随机高斯值。 最后一个隐藏层后面是一个完全连接的层，有10个激活（每个类一个）和交叉熵损失。 我们对网络进行了50000个步骤的训练，每个小批有60个例子。 我们将批处理规范化添加到网络的每个隐藏层中，如SEC所示。 3.1. 我们感兴趣的是基线网络和批归一化网络之间的比较，而不是在MNIST（描述的体系结构没有)上实现最先进的性能状态）。图1(A)显示了随着训练的进展，两个网络对暂停测试数据的正确预测的分数。 批量归一化网络具有较高的测试精度。 为了研究为什么，我们研究了输入到乙状结肠，在原始网络N和批归一化网络NTRBN(Alg。 在训练过程中2)。 在图中。 我们展示了1(b，c)，对于每个网络的最后一个隐藏层的一个典型激活，它的分布是如何演变的。 随着时间的推移，原始网络中的分布在均值和方差上都有显著的变化，这使得后续层的训练复杂化。 相反，随着训练的进展，批归一化网络中的分布更加稳定，这有助于训练。
4.2图像网分类
我们将批处理规范化应用于Inception网络的一个新变体(Szegedy et al., 2014),像对图网分类任务进行了培训(Russakovsky et al., 2014) 网络有大量的卷积层和池层，用softmax层来预测图像类，有1000种可能性。 卷积层采用ReLU作为非线性。 所述网络的主要区别(Szegedy et al., 2014) 是将5×5卷积层替换为两个连续的3×3卷积层，其滤波器可达128个。 网络包含13.6·106个参数，除了顶层Softmax层之外，没有完全连接的层。详情见附录。 在本文的其余部分中，我们将此模型称为Inception。 该模型使用具有动量的随机梯度下降的版本进行训练(Sutskever et al., 2013), ，使用32的小批量大小。 培训是使用大规模分布式架构进行的（类似于(Dean et al., 2012)）通过计算验证精度@1，即，对所有网络进行评估。 在一个搁置的集合上，使用每幅图像的单个作物，从1000种可能性中预测正确标签的概率。
在我们的实验中，我们评估了几个修改的初始与批量归一化。 在所有情况下，批归一化都以卷积的方式应用于每个非线性的输入，如第3.2节所述，同时保持体系结构的其余部分不变。
4.2.1加速BN网络
简单地将批处理规范化添加到网络中并不能充分利用我们的方法。 为此，我们进一步改变了网络及其训练参数，具体如下：提高学习率。 在批量标准化模型中，我们已经能够从更高的学习率中实现训练速度的提高，没有不良的副作用(SEC。 3.3)。 移除Dropout。 如证券交易委员会所述。 3.4，批量标准化实现了与Dropout相同的一些目标。 从修改后的BN-接收中移除辍学加速了训练，而不增加过度拟合。减少L2权重正则化。 在初始阶段，模型参数上的L2损失控制过拟合，而在修改后的BN-初始阶段，这种损失的重量减少了5倍。 我们发现，这提高了搁置验证数据的准确性。 加速学习速率衰减。 在训练中，学习率呈指数衰减。 因为我们的网络训练比Inception快，所以我们把学习速度降低了6倍。在启动和其他网络时删除本地响应规范化(Srivastava et al., 2014) 从它的好处，我们发现，与批量归一化是不必要的。shuffle训练例子更彻底。 我们启用了延迟内洗牌的训练数据，这防止了相同的例子总是出现在一个小批一起。 这导致了大约1%的验证精度的提高，这与批规范化作为正则化的观点是一致的(SEC。 3.4)：我们的方法中固有的随机化应该是最有益的，当它每次看到一个例子时都会对它产生不同的影响。减少光度扭曲。 由于批量标准化网络训练速度更快，观察每个训练示例的次数也更少，所以我们让培训师通过更少地扭曲它们来关注更多的“真实”图像。

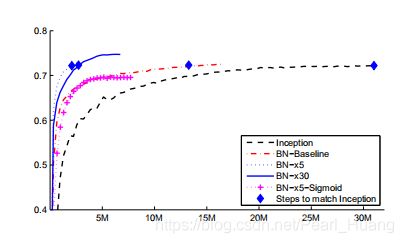
图2：Inception及其批归一化变体的单作物验证精度与训练步骤的数量
4.2.2单网络分类
我们评估了以下网络，所有这些网络都是在LSVRC2012培训数据上进行培训的，并在验证数据上进行了测试：
Inception：在4.2节开始时描述的网络，培训的初始学习率为0.0015。
BN-Baseline：与每次非线性前具有批归一化的初始相同。
BN-x5：批量归一化的初始化和SEC中的修改。 4.2.1. 初始学习率提高了5倍，达到0.0075。 相同的学习速率随原始初始的增加而增加，使模型参数达到机器无穷大
BN-x5-Sigmoid：类似于BN-x5，但具有Sigmoid非线性
而不是ReLU。 我们还尝试用Sigmoid训练原始的Inception，但模型保持了与偶然相等的精度。
在图2中，我们显示了网络的验证精度，作为训练步骤数的函数。 在31·106个训练步骤后，盗梦空间的准确率达到了72.2。 图3显示了对于每个网络，达到相同的72.2%精度所需的培训步骤数，以及网络达到的最大验证精度和达到的步骤数。
通过只使用批归一化(BN-基线)，我们在不到一半的训练步骤中匹配Inception的准确性。 通过应用SEC中的修改。 4.2.1，我们显著提高了网络的训练速度。 BN-x5需要比Inception少14倍的步骤才能达到72.2%的精度。 有趣的是，进一步提高学习速率(BN-x30)会使模型最初的训练速度略慢，但允许它达到更高的最终精度。 经6·106步后达到74.8。 比Inception要求的步骤少5倍，达到72.2%。
我们还验证了内部协变量移位的减少允许具有批归一化的深层网络

图3：对于Inception和批归一化变体，要达到Inception的最大精度（72.2%)所需的），以及网络实现的最大精度。当s型被用作非线性时，尽管训练这种网络是众所周知的困难。 事实上，BN-x5-Sigmoid的准确率达到69.8%。 如果没有批处理规范化，Sigmoid的初始化永远不会达到超过千分之一的精度
4.2.3装配分类
传统模型的深度图像集成技术在图像网大规模视觉识别竞赛中取得了较好的效果(Wu et al., 2015) 的集合模型(He et al., 2015) 后者报告的前5个错误为4.94%，由ILSVRC服务器评估。 在这里，我们报告了4.9%的前5验证错误和4.82%的测试错误(根据ILSVRC服务器)。 这改善了以前的最佳结果，并超过了估计的准确性，根据人类评分者(Russakovsky et al., 2014). 对于我们的集合，我们使用了6个网络。 每种方法都是基于BN-x30，通过以下几种方法进行修改：增加卷积层中的初始权重；使用Dropout(Dropout概率为5%或10%，而原始Inception为40%)；使用非卷积、每激活批归一化和模型的最后隐藏层。 每个网络经过大约6·106个训练步骤，达到了最大的精度。 集合预测是基于由组成网络预测的类概率的算术平均值。 系综和多播推理的细节相似(Szegedy et al., 2014). 我们在图中演示。 该批规范化允许我们在Image Net分类挑战基准上以健康的边缘设置新的最先进的状态。
5结论
我们提出了一种新的机制来显着地加速深度网络的训练。 它是基于协变量移位的前提，它已知使机器学习系统的训练复杂化，根据到子网络和层，并将其从网络的内部激活中删除，可能有助于培训。 我们提出的方法从规范化激活和将这种规范化纳入网络体系结构本身中汲取了它的力量。 这确保规范化被用于训练网络的任何优化方法适当地处理。 为了实现深度网络训练中常用的随机优化方法，我们对每个小批进行归一化，并通过归一化参数反向传播梯度。 批处理规范化每次激活只增加两个额外的参数，这样可以保持网络的表示能力。 我们提出了一种用批归一化网络构造、训练和执行推理的算法。 由此产生的网络可以用饱和非线性训练，更能容忍训练速率的增加，并且通常不需要退出进行正则化。

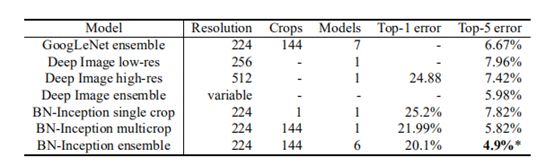
仅仅将批处理规范化添加到最先进的图像分类模型中，可以大大加快训练速度。 通过进一步提高学习率，删除辍学，并应用批量归一化提供的其他修改，我们只需要一小部分训练步骤就能达到以前的艺术状态-然后在单网络图像分类中击败了最先进的状态。 此外，通过将多个模型与批归一化相结合，我们在图像网上的性能优于最著名的系统，具有很大的优势。
有趣的是，我们的方法与标准化层具有相似性(G¨ulc¸ehre & Bengio, 2013) 虽然这两种方法源于非常不同的目标，并执行不同的任务。 批归一化的目标是在整个训练过程中实现激活值的稳定分布，在我们的实验中，我们在非线性之前应用它，因为匹配第一和第二矩更有可能导致稳定的分布。 恰恰相反(G¨ulc¸ehre & Bengio, 2013) 将标准化层应用于非线性的输出，从而导致稀疏激活。 在我们的大规模图像分类实验中，我们没有观察到非线性输入是稀疏的，既没有也没有批归一化。其他显著差异批归一化的特性包括允许BN变换表示标识的学习尺度和移位（标准化层不需要这样做，因为它后面是学习的线性变换，在概念上吸收必要的尺度和移位）、处理卷积层、不依赖于小批处理的确定性推理以及对网络中每个卷积层的批处理。在这项工作中，我们还没有探索批处理规范化可能实现的全部可能性。 我们未来的工作包括我们的方法在递归神经网络中的应用(Pascanu et al., 2013) 其中内部协变量位移和消失或爆炸梯度可能特别严重，这将使我们能够更彻底地检验归一化改善梯度传播的假设(SEC。 3.3)。 我们计划调查批量规范化是否有助于领域适应，在其传统意义上-即。 网络执行的规范化是否会使它更容易地推广到新的数据分布，也许只是重新计算总体均值和方差(Alg。 2)。 最后，我们认为对该算法的进一步理论分析将允许更多的改进和应用。
参考
Bengio, Yoshua and Glorot, Xavier. Understanding the diffificulty of training deep feedforward neural networks. In Proceedings of AISTATS 2010, volume 9, pp. 249– 256, May 2010.
Dean, Jeffrey, Corrado, Greg S., Monga, Rajat, Chen, Kai, Devin, Matthieu, Le, Quoc V., Mao, Mark Z., Ranzato, Marc’Aurelio, Senior, Andrew, Tucker, Paul, Yang, Ke, and Ng, Andrew Y. Large scale distributed deep networks. In NIPS, 2012.
Desjardins, Guillaume and Kavukcuoglu, Koray. Natural neural networks. (unpublished). Duchi, John,Hazan, Elad, and Singer, Yoram. Adaptive subgradient methods for online learning and stochastic 8optimization. J. Mach. Learn. Res., 12:2121–2159, July 2011. ISSN 1532-4435.
G¨ulc¸ehre, C¸ aglar and Bengio, Yoshua. Knowledge matters: Importance of prior information for optimization. CoRR, abs/1301.4083, 2013.
He, K., Zhang, X., Ren, S., and Sun, J. Delving Deep into Rectififiers: Surpassing Human-Level Performance on ImageNet Classifification. ArXiv e-prints, February 2015.
Hyv¨arinen, A. and Oja, E. Independent component analysis: Algorithms and applications. Neural Netw., 13 (4-5):411–430, May 2000.
Jiang, Jing. A literature survey on domain adaptation of statistical classififiers, 2008.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, November 1998a.
LeCun, Y., Bottou, L., Orr, G., and Muller, K. Effificient backprop. In Orr, G. and K., Muller (eds.), Neural Networks: Tricks of the trade. Springer, 1998b.
Lyu, S and Simoncelli, E P. Nonlinear image representation using divisive normalization. In Proc. Computer Vision and Pattern Recognition, pp. 1–8. IEEE Computer Society, Jun 23-28 2008. doi: 10.1109/CVPR. 2008.4587821.
Nair, Vinod and Hinton, Geoffrey E. Rectifified linear units improve restricted boltzmann machines. In ICML, pp. 807–814. Omnipress, 2010.
Pascanu, Razvan, Mikolov, Tomas, and Bengio, Yoshua. On the diffificulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning, ICML 2013,Atlanta, GA, USA, 16- 21 June 2013, pp. 1310–1318, 2013.
Povey, Daniel, Zhang, Xiaohui, and Khudanpur, Sanjeev. Parallel training of deep neural networks with natural gradient and parameter averaging. CoRR, abs/1410.7455, 2014.
Raiko, Tapani, Valpola, Harri, and LeCun, Yann. Deep learning made easier by linear transformations in perceptrons. In International Conference on Artifificial Intelligence and Statistics (AISTATS), pp. 924–932, 2012.
Russakovsky, Olga, Deng, Jia, Su, Hao, Krause, Jonathan, Satheesh, Sanjeev, Ma, Sean, Huang, Zhiheng, Karpathy, Andrej, Khosla, Aditya, Bernstein, Michael, Berg, Alexander C., and Fei-Fei, Li. ImageNet Large Scale Visual Recognition Challenge, 2014.
Saxe, Andrew M., McClelland, James L., and Ganguli, Surya. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. CoRR, abs/1312.6120, 2013.
Shimodaira, Hidetoshi. Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference, 90(2):227–244, October 2000.
Srivastava, Nitish, Hinton, Geoffrey, Krizhevsky, Alex, Sutskever, Ilya, and Salakhutdinov, Ruslan. Dropout: A simple way to prevent neural networks from overfifitting. J. Mach. Learn. Res.,15(1):1929–1958, January 2014.
Sutskever, Ilya, Martens, James, Dahl, George E., and Hinton, Geoffrey E. On the importance of initialization and momentum in deep learning. In ICML (3), volume 28 of JMLR Proceedings, pp. 1139–1147. JMLR.org, 2013.
Szegedy, Christian, Liu, Wei, Jia, Yangqing, Sermanet, Pierre, Reed, Scott, Anguelov, Dragomir, Erhan, Dumitru, Vanhoucke, Vincent, and Rabinovich, Andrew. Going deeper with convolutions.
CoRR, abs/1409.4842, 2014.
Wiesler, Simon and Ney, Hermann. A convergence analysis of log-linear training. In Shawe-Taylor, J., Zemel, R.S., Bartlett, P., Pereira, F.C.N., and Weinberger, K.Q. (eds.), Advances in Neural Information Processing Systems 24, pp. 657–665, Granada, Spain, December 2011.
Wiesler, Simon, Richard, Alexander, Schl¨uter, Ralf, and Ney, Hermann. Mean-normalized stochastic gradient for large-scale deep learning. In IEEE International Conference on Acoustics, Speech, and Signal Processing, pp. 180–184, Florence, Italy, May 2014.
Wu, Ren, Yan, Shengen, Shan, Yi, Dang, Qingqing, and Sun, Gang. Deep image: Scaling up imagerecognition, 2015.
附录
所使用的初始模型的变体
图5记录了相对于Google Net架构进行的更改。 关于本表的解释，请查阅(Szegedy等人，2014年)。 与Google LeNet模型相比，显著的体系结构变化包括：将5×5个卷积层替换为两个连续的3×3个卷积层。 这使网络的最大深度增加了9个9重层。 它还增加了25%的参数，计算成本增加了30%左右%。
从2到3。 增加了28×28个起始模块
在模块内部，有时采用平均池，有时采用最大池。 这在表的池层对应的条目中表示。
在任何两个Inception模块之间没有跨板池层，但在模块3c、4e中的滤波器级联之前，使用了stage-2卷积/池层。
我们的模型在第一卷积层上采用了深度乘法器8的可分离卷积。 这降低了计算成本，同时增加了训练时的内存消耗。

学习记录

参考资料： Batch Normalization原理与实战
在卷积网络六大模块中的BN（批批标准化）所指的就是Batch Normalization，该算法15年提出，现在已经成为深度学习中经常使用的技术，可以极大的提高网络的处理能力。
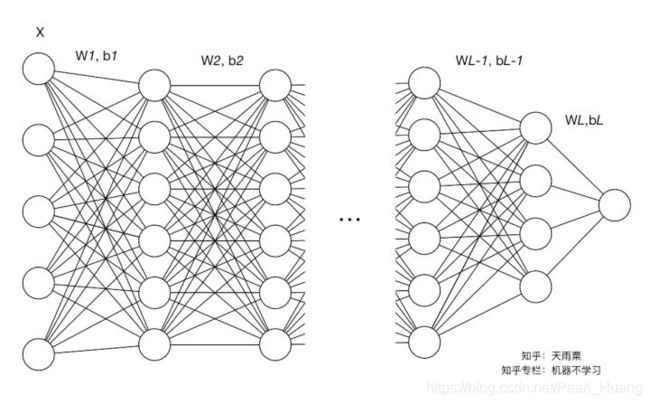
如论文指出：在深度学习中，由于问题的复杂性，我们往往会使用较深层数的网络进行训练，在这个过程中，尤其是对深层神经网络的训练调参。我们需要去尝试不同的学习率、初始化参数方法（例如Xavier初始化）等方式来帮助我们的模型加速收敛。深度神经网络之所以如此难训练，其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。

内部协方差移位

Batch Normalization的原论文作者给了Internal Covariate Shift一个较规范的定义：在深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。

Internal Covariate Shift会带来的问题

（1）上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低
（2）网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度

解决Internal Covariate Shift会带来的问题方法和弊病

要缓解ICS的问题，就要明白它产生的原因。ICS产生的原因是由于参数更新带来的网络中每一层输入值分布的改变，并且随着网络层数的加深而变得更加严重，因此我们可以通过固定每一层网络输入值的分布来对减缓ICS问题。

当时提出的解决方法

（1）白化（Whitening）
白化（Whitening）是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换，进而达到以下两个目的：
1.使得输入特征分布具有相同的均值与方差。其中PCA白化保证了所有特征分布均值为0，方差为1；而ZCA白化则保证了所有特征分布均值为0，方差相同；
2.去除特征之间的相关性。
通过白化操作，我们可以减缓ICS的问题，进而固定了每一层网络输入分布，加速网络训练过程的收敛（LeCun et al.,1998b；Wiesler&Ney,2011）。
白化主要有以下两个问题：
1.白化过程计算成本太高，并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作；
2.白化过程由于改变了网络每一层的分布，因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
既然有了上面两个问题，那我们的解决思路就很简单，一方面，我们提出的normalization方法要能够简化计算过程；另一方面又需要经过规范化处理后让数据尽可能保留原始的表达能力。于是就有了简化+改进版的白化——Batch Normalization。

Batch Normalization的思路

既然白化计算过程比较复杂，那我们就简化一点，比如我们可以尝试单独对每个特征进行normalizaiton就可以了，让每个特征都有均值为0，方差为1的分布就OK。

另一个问题，既然白化操作减弱了网络中每一层输入数据表达能力，那我就再加个线性变换操作，让这些数据再能够尽可能恢复本身的表达能力就好了。

因此，基于上面两个解决问题的思路，作者提出了Batch Normalization

算法思路

在深度学习中，由于采用full batch的训练方式对内存要求较大，且每一轮训练时间过长；我们一般都会采用对数据做划分，用mini-batch对网络进行训练。因此，Batch Normalization也就在mini-batch的基础上进行计算。

使用小样本的例子，而不是一次一个例子，在几个方面是有帮助的。 首先，小批损失的梯度是训练集上梯度的估计，随着批处理大小的增加，训练集的质量提高。 其次，由于现代计算平台提供的并行性，批处理上的计算可以比单个示例的m计算更有效。——原论文

算法步骤

Batch Normalization的优势

（1）BN使得网络中每层输入数据的分布相对稳定，加速模型学习速度
（2）BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定
在神经网络中，我们经常会谨慎地采用一些权重初始化方法（例如Xavier）或者合适的学习率来保证网络稳定训练。

注：公式中的 u 是当前层的输入，也是前一层的输出

（3）BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题
（4）BN具有一定的正则化效果
在Batch Normalization中，由于我们使用mini-batch的均值与方差作为对整体训练样本均值与方差的估计，尽管每一个batch中的数据都是从总体样本中抽样得到，但不同mini-batch的均值与方差会有所不同，这就为网络的学习过程中增加了随机噪音，与Dropout通过关闭神经元给网络训练带来噪音类似，在一定程度上对模型起到了正则化的效果。

另外，原作者通过也证明了网络加入BN后，可以丢弃Dropout，模型也同样具有很好的泛化效果。

再看BN应用

参考资料: BN(Batch Normalization) 原理与使用过程详解

BN层是如何实现的

从论文中给出的伪代码可以看出来BN层的计算流程是：

1.计算样本均值。

2.计算样本方差。

3.样本数据标准化处理。

4.进行平移和缩放处理。引入了γ和β两个参数。来训练γ和β两个参数。引入了这个可学习重构参数γ、β，让我们的网络可以学习恢复出原始网络所要学习的特征分布。

卷积过程可以得出一张55的图片经过卷积核33的卷积之后得到一张33的特征图。特征图就会包含了9个特征值，这9个特征值就是我们上面所提到的样本。假设我们的batch-size设为m，那么就会有m9个特征值传到BN层里面作为样本来训练参数γ和β。

在网络训练中以batch-size作为最小单位来不断迭代。每当有新的batch-size进入到网络里面就会产生新的γ和β。也就是说我们训练过程中要生成 图片总量/batch-size 组参数。

图像卷积的过程中，通常是使用多个卷积核，得到多张特征图，对于多个的卷积核需要保存多个的γ与β。

BN层的整体流程如下图：

输入：待进入激活函数的变量
输出：
1.这里的K，在卷积网络中可以看作是卷积核个数，如网络中第n层有64个卷积核，就需要计算64次。
需要注意，在正向传播时，会使用γ与β使得BN层输出与输入一样。
2.在反向传播时利用γ与β求得梯度从而改变训练权值（变量）。
3.通过不断迭代直到训练结束，求得关于不同层的γ与β。
4.不断遍历训练集中的图片，取出每个batch_size中的γ与β，最后统计每层BN的γ与β各自的和除以图片数量得到平均直，并对其做无偏估计值作为每一层的E[x]与Var[x]。
5.在预测的正向传播时，对测试数据求取γ与β，并使用该层的E[x]与Var[x]，通过图中所表示的公式计算BN层输出。
注意，在预测时，BN层的输出已经被改变，所以BN层在预测的作用体现在此处。

用法总结

链接: 批标准化（Batch Normalization）总结