ML/DL学习笔记3——梯度下降Gradient Descent

课程链接

什么是梯度？

    梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

    通俗的来说梯度是要解决这么一个问题
    函数在变量空间(变量的维度可能很高)的某一点，沿着那个方向有最大的变化率？梯度退化到xoy平面的二维空间，其实就是导数的概念。

    需要注意如下几点：
    1.梯度是一个向量，既有大小又有方向。
    2.梯度的方向是最大方向导数的方向。
    3.梯度的模是方向导数的最大值。

    为什么说梯度方向与等高线切线方向垂直
    推导了一下附上截图哈哈（字有点丑-_-）

回顾

    前面预测宝可梦cp值的例子里，已经初步介绍了Gradient Descent的用法：

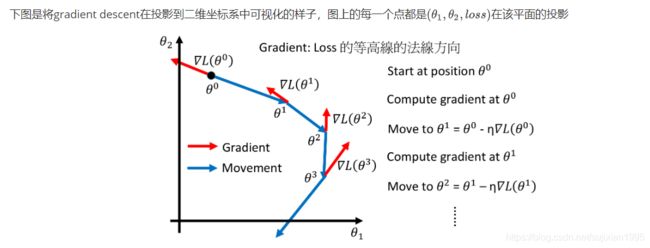
    红色箭头是指在(${\theta }_1$,${\theta }_2$)这点的梯度，梯度方向即箭头方向(从低处指向高处)，梯度大小即箭头长度(表示在${\theta }^i$点处最陡的那条切线的导数大小，该方向也是梯度上升最快的方向)

    因此，在整个gradient descent的过程中，梯度不一定是递减的(红色箭头的长度可以长短不一)，但是沿着梯度下降的方向，函数值loss一定是递减的，且当gradient=0时，loss下降到了局部最小值，总结：梯度下降法指的是函数值loss随梯度下降的方向减小

    初始随机在三维坐标系中选取一个点，这个三维坐标系的三个变量分别为(${\theta }_1$,${\theta }_2$,loss)，我们的目标是找到最小的那个loss也就是三维坐标系中高度最低的那个点，而gradient梯度可以理解为高度上升最快的那个方向，它的反方向就是梯度下降最快的那个方向，于是每次update沿着梯度反方向，update的步长由梯度大小和learning rate共同决定，当某次update完成后，该点的gradient=0，说明到达了局部最小值

Learning rate存在的问题

gradient descent过程中，影响结果的一个很关键的因素就是learning rate的大小
    (1)如果learning rate刚刚好，就可以像下图中红色线段一样顺利地到达到loss的最小值
    (2)如果learning rate太小的话，像下图中的蓝色线段，虽然最后能够走到local minimal的地方，但是
    它可能会走得非常慢，以至于你无法接受
    (3)如果learning rate太大，像下图中的绿色线段，它的步伐太大了，它永远没有办法走到特别低的
    地方，可能永远在这个“山谷”的口上振荡而无法走下去
    (4)如果learning rate非常大，就会像下图中的黄色线段，一瞬间就飞出去了，结果会造成update参
    数以后，loss反而会越来越大(这一点在上次的demo中有体会到，当lr过大的时候，每次更新loss反
    而会变大)

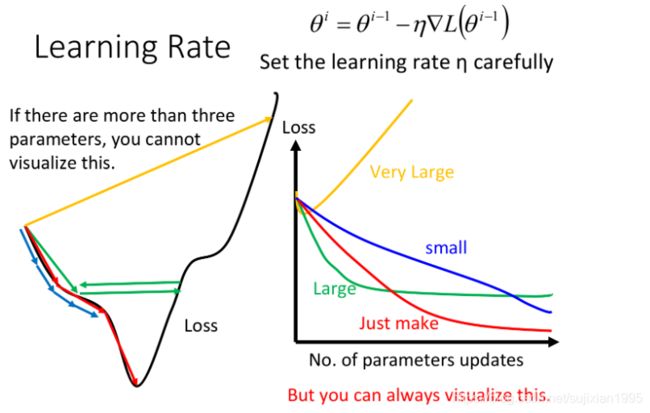
当参数有很多个的时候(>3)，其实我们很难做到将loss随每个参数的变化可视化出来(因为最多只能可视化出三维的图像，也就只能可视化三维参数)，但是我们可以把update的次数作为唯一的一个参数，将loss随着update的增加而变化的趋势给可视化出来(上图右半部分)

所以做gradient descent一个很重要的事情是，要把不同的learning rate下，loss随update次数的变化曲线给可视化出来，它可以提醒你该如何调整当前的learning rate的大小，直到出现稳定下降的曲线

Adaptive Learning rates(自适应学习率)

手动去调节学习率是一件很麻烦的事情我们需要一种自动调节学习率的方法

最基本、最简单的大原则是：learning rate通常是随着参数的update越来越小的

因为在起始点的时候，通常是离最低点是比较远的，这时候步伐就要跨大一点；而经过几次update以后，会比较靠近目标，这时候就应该减小learning rate，让它能够收敛在最低点的地方

举例：假设到了第t次update，此时：

这种方法使所有参数以同样的方式同样的learning rate进行update，而最好的状况是每个参数都给他不同的learning rate去update

Adagrad
Adagrad就是将不同参数的learning rate分开考虑的一种算法(adagrad算法update到后面速度会越来越慢，当然这只是adaptive算法中最简单的一种)

这里的w是function中的某个参数，t表示第t次update，$g^t$表示Loss对w的偏微分，而${\sigma }^t$是之前所有Loss对w偏微分的均方根(根号下的平方均值)，这个值对每一个参数来说都是不一样的

Adagrad的矛盾解释

Adagrad的表达式有一个矛盾的地方，就是偏微分越大参数应该变化越大，但是偏微分越大分母(均方根)也就越大那么参数的变化又会变小似乎是矛盾了这是为什么呢？

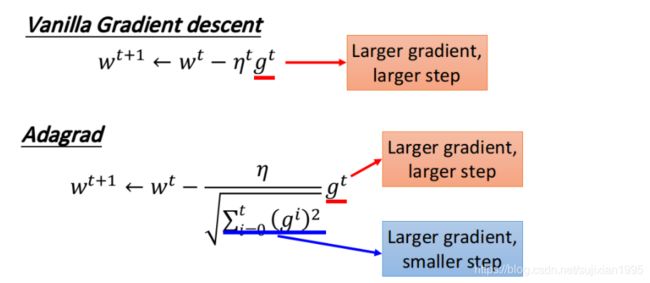
在一些paper里是这样解释的：Adagrad要考虑的是，这个gradient有多surprise，即反差有多大，假设t=4的时候$g^4$与前面的gradient反差特别大，那么$g^t$与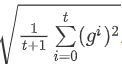
之间的大小反差就会比较大，它们的商就会把这一反差效果体现出来(没太明白再研究研究)

gradient越大，离最低点越远这件事情在有多个参数的情况下是不一定成立的

如下图所示，w1和w2分别是loss function的两个参数，loss的值投影到该平面中以颜色深度表示大小，分别在w2和w1处垂直切一刀(控制变量)，对应的情况为右边的两条曲线，可以看出，比起a点，c点距离最低点更近，但是它的gradient却越大

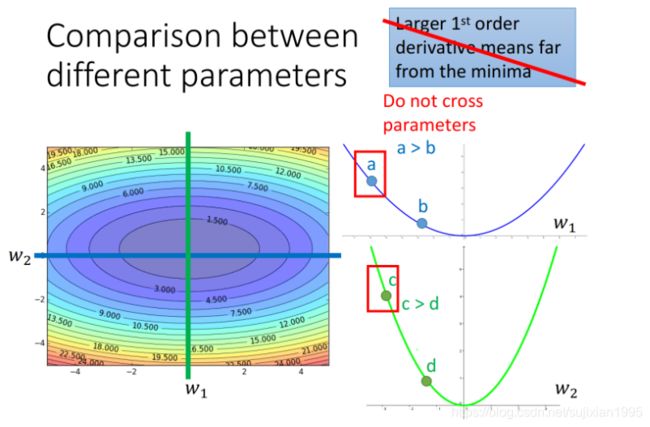
从图中可以看出绿色线中等高线变换越密集说明越陡峭，偏微分越大。

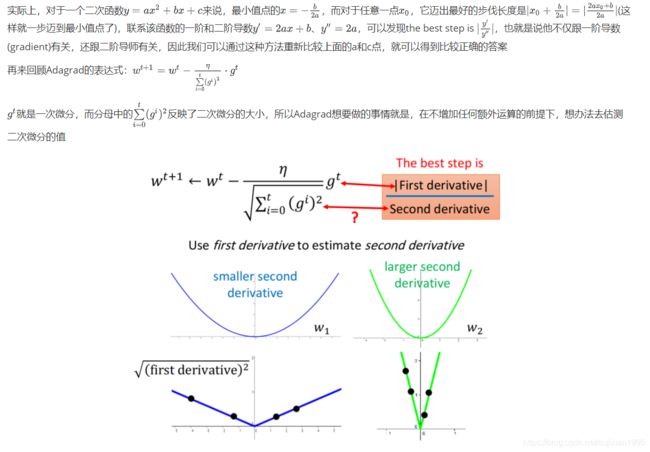
为什么均方根可以估计二次微分呢没搞明白

Stochastic Gradicent Descent（随机梯度下降法）

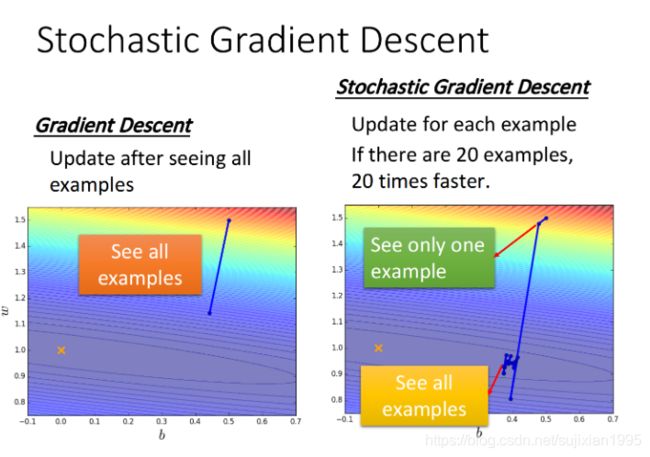
随机梯度下降的方法可以让训练更快速，传统的gradient descent的思路是看完所有的样本点之后再构建loss function，然后去update参数；而stochastic gradient descent的做法是，看到一个样本点就update一次，因此它的loss function不是所有样本点的error平方和，而是这个随机样本点的error平方

stochastic gradient descent与传统gradient descent的效果对比如下：

Feature Scaling（特征缩放）

概念介绍
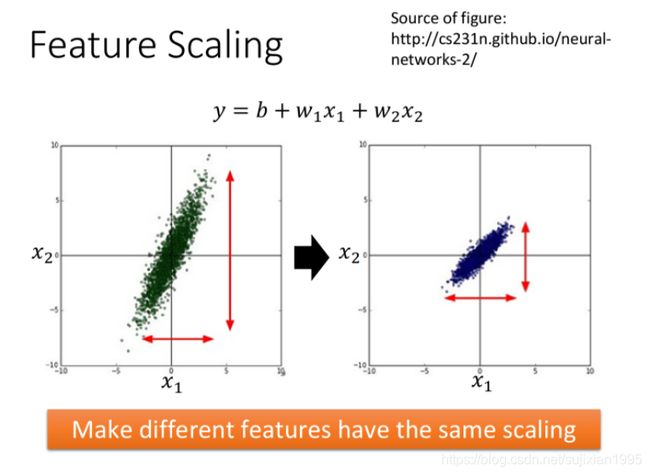
特征缩放，当多个特征的分布范围很不一样时，最好将这些不同feature的范围缩放成一样

原理解释
$y=b+w_1{x}_1+w_1{x}_2$,设x1的值都是很小的，比如1,2…；x2的值都是很大的，比如100,200…此时去画出loss的error surface，如果对w1和w2都做一个同样的变动$\Delta w$，那么w1的变化对y的影响是比较小的，而w2的变化对y的影响是比较大的

左边的error surface表示，w1对y的影响比较小，所以w1对loss是有比较小的偏微分的，因此在w1的方向上图像是比较平滑的；w2对y的影响比较大，所以w2对loss的影响比较大，因此在w2的方向上图像是比较sharp的
如果x1和x2的值，它们的scale是接近的，那么w1和w2对loss就会有差不多的影响力，loss的图像接近于圆形，那这样做对gradient descent有什么好处呢？

对gradient decent的帮助

之前我们做的demo已经表明了，对于这种长椭圆形的error surface，如果不使用Adagrad之类的方法，是很难搞定它的，因为在像w1和w2这样不同的参数方向上，会需要不同的learning rate，用相同的lr很难达到最低点

如果有scale的话，loss在参数w1、w2平面上的投影就是一个正圆形，update参数会比较容易

而且gradient descent的每次update并不都是向着最低点走的，每次update的方向是顺着等高线的方向(梯度gradient下降的方向)，而不是径直走向最低点；但是当经过对input的scale使loss的投影是一个正圆的话，不管在这个区域的哪一个点，它都会向着圆心走。因此feature scaling对参数update的效率是有帮助的

如何做feature scaling(后面的内容都是数学的知识可以不用理解大体知道过程就可以了)

这里没有弄明白后面有时间再学习一下

Gradient Descent的理论基础

Taylor Series(泰勒级数)




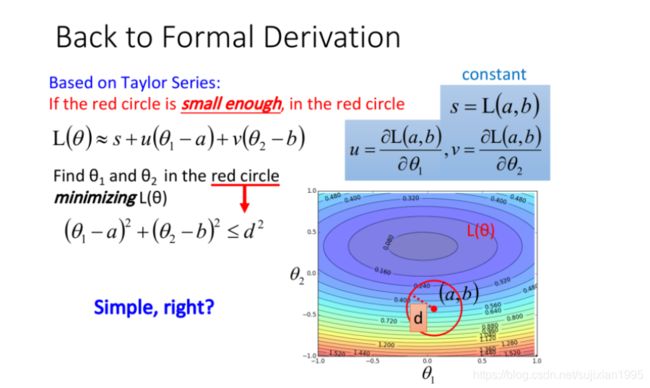
Gradient Descent的限制

之前已经讨论过，gradient descent有一个问题是它会停在local minima的地方就停止update了

事实上还有一个问题是，微分值是0的地方并不是只有local minima，settle point的微分值也是0
以上都是理论上的探讨，到了实践的时候，其实当gradient的值接近于0的时候，我们就已经把它停下来了，但是微分值很小，不见得就是很接近local minima，也有可能像下图一样在一个高原的地方

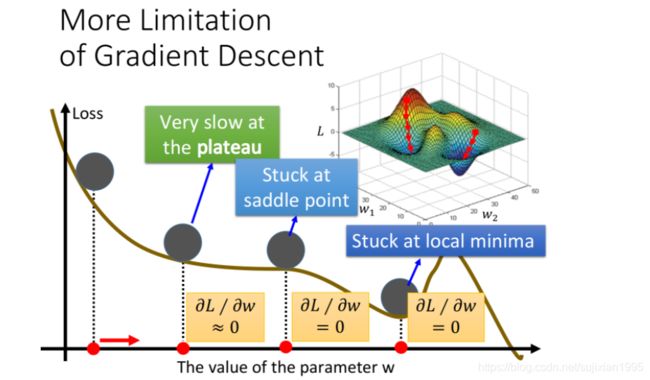
所以说梯度下降的限制是：通过梯度下降方法找到的loss最小的点不一定是全局最小值还有可能是局部最小值或者鞍点甚至是loss值很高的平缓高原plateau

例子代码

用gradient descent把b和w找出来
这里采用最简单的linear model：y_data=b+w*x_data

需要引入的库文件
运行程序时会报错将引入的 Agg 改成TKAgg即可使用

import matplotlib
import matplotlib.pyplot as plt
matplotlib.use('TKAgg')
import random as random
import numpy as np
import csv

数据准备

# 假设x_data和y_data都有10笔，分别代表宝可梦进化前后的cp值
x_data=[338.,333.,328.,207.,226.,25.,179.,60.,208.,606.]
y_data=[640.,633.,619.,393.,428.,27.,193.,66.,226.,1591.]
# 这里采用最简单的linear model：y_data=b+w*x_data
# 我们要用gradient descent把b和w找出来

准备好b、w、loss的图像数据

# 生成一组b和w的数据图，方便给gradient descent的过程做标记
x = np.arange(-200,-100,1) # bias
y = np.arange(-5,5,0.1) # weight
Z = np.zeros((len(x),len(y))) # color
X,Y = np.meshgrid(x,y)
for i in range(len(x)):
    for j in range(len(y)):
        b = x[i]
        w = y[j]
        
        # Z[j][i]存储的是loss
        Z[j][i] = 0
        for n in range(len(x_data)):
            Z[j][i] = Z[j][i] + (y_data[n] - (b + w * x_data[n]))**2
        Z[j][i] = Z[j][i]/len(x_data)

计算梯度微分的函数getGrad()

# 计算梯度微分的函数getGrad()
def getGrad(b,w):
    # initial b_grad and w_grad
    b_grad=0.0
    w_grad=0.0
    for i in range(10):
        b_grad+=(-2.0)*(y_data[i]-(b+w*x_data[i]))
        w_grad+=(-2.0*x_data[i])*(y_data[i]-(b+w*x_data[i]))
    return (b_grad,w_grad)

规定迭代次数和learning rate，进行第一次尝试

# y_data = b + w * x_data
b = -120 # initial b
w = -4 # initial w
lr = 0.0000001 # learning rate
iteration = 100000 # 这里直接规定了迭代次数，而不是一直运行到b_grad和w_grad都为0(事实证明这样做不太可行)
​
# store initial values for plotting，我们想要最终把数据描绘在图上，因此存储过程数据
b_history = [b]
w_history = [w]
​
# iterations
for i in range(iteration):
    
    # get new b_grad and w_grad
    b_grad,w_grad=getGrad(b,w)
    
    # update b and w
    b -= lr * b_grad
    w -= lr * w_grad
    
    #store parameters for plotting
    b_history.append(b)
    w_history.append(w)
​
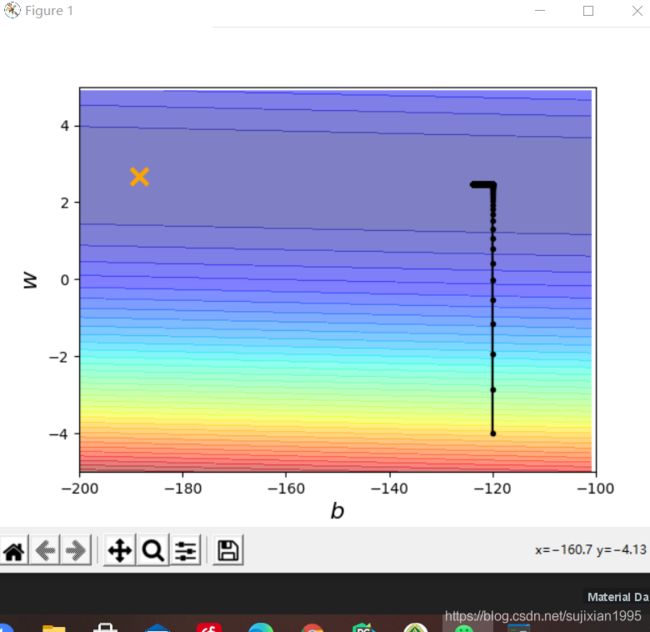
# plot the figure
plt.contourf(x,y,Z,50,alpha=0.5,cmap=plt.get_cmap('jet'))
plt.plot([-188.4],[2.67],'x',ms=12,markeredgewidth=3,color='orange')
plt.plot(b_history,w_history,'o-',ms=3,lw=1.5,color='black')
plt.xlim(-200,-100)
plt.ylim(-5,5)
plt.xlabel(r'$b$',fontsize=16)
plt.ylabel(r'$w$',fontsize=16)
plt.show()

距离黄色叉号位置还有很大的距离

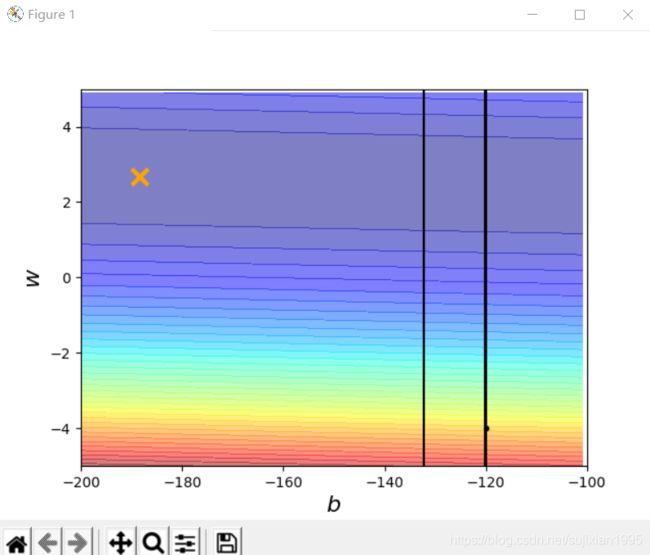
将学习率增大十倍

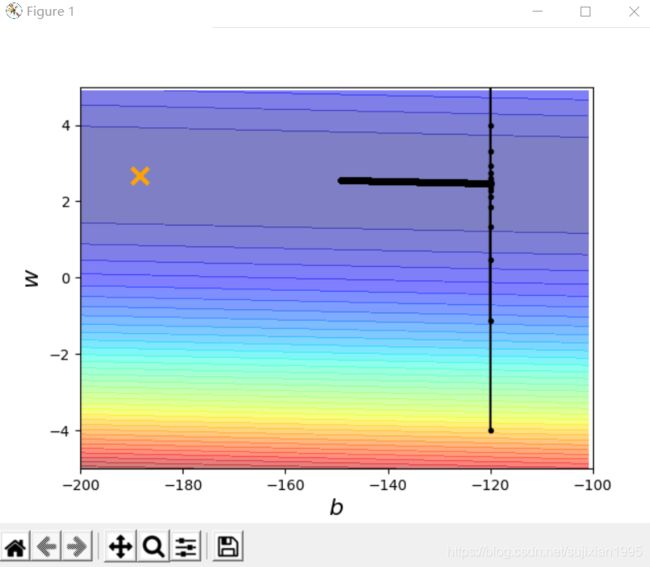
我们发现距离目标距离更近了一步但是出现了剧烈的上下震荡

继续增大学习率变为原来的十倍

超出了标注范围，烂掉了

b和w，gradient descent搞半天都搞不定，这里我们用Adagrad

让w和b它们两个的learning rate不一样

# 这里给b和w不同的learning rate

# y_data = b + w * x_data
b = -120  # initial b
w = -4  # initial w
lr = 1  # learning rate 放大10倍
iteration = 100000  # 这里直接规定了迭代次数，而不是一直运行到b_grad和w_grad都为0(事实证明这样做不太可行)

# store initial values for plotting，我们想要最终把数据描绘在图上，因此存储过程数据
b_history = [b]
w_history = [w]

lr_b = 0
lr_w = 0

# iterations
for i in range(iteration):
    # get new b_grad and w_grad
    b_grad, w_grad = getGrad(b, w)

    # get the different learning rate for b and w
    lr_b = lr_b + b_grad ** 2
    lr_w = lr_w + w_grad ** 2

    # 这一招叫做adagrad，之后会详加解释
    # update b and w with new learning rate
    b -= lr / np.sqrt(lr_b) * b_grad
    w -= lr / np.sqrt(lr_w) * w_grad

    # store parameters for plotting
    b_history.append(b)
    w_history.append(w)

    # output the b w b_grad w_grad
    # print("b: "+str(b)+"\t\t\t w: "+str(w)+"\n"+"b_grad: "+str(b_grad)+"\t\t w_grad: "+str(w_grad)+"\n")

# output the final function and its error
print("the function will be y_data=" + str(b) + "+" + str(w) + "*x_data")
error = 0.0
for i in range(10):
    print("error " + str(i) + " is: " + str(np.abs(y_data[i] - (b + w * x_data[i]))) + " ")
    error += np.abs(y_data[i] - (b + w * x_data[i]))
average_error = error / 10
print("the average error is " + str(average_error))

# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet'))
plt.plot([-188.4], [2.67], 'x', ms=12, markeredgewidth=3, color='orange')
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$', fontsize=16)
plt.ylabel(r'$w$', fontsize=16)
plt.show()