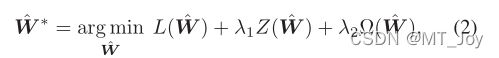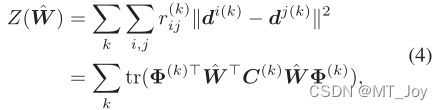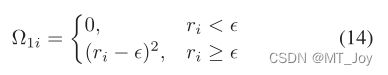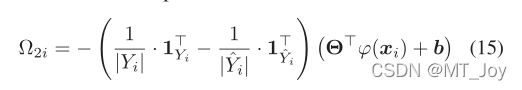Partial Multi-Label Learning with Label Distribution-(PML-LD)-文献翻译

 论文链接：Partial Multi-Label Learning with Label Distribution | Proceedings of the AAAI Conference on Artificial Intelligence

                                                                AAAI-2020

摘要

        部分多标签学习（PML）旨在从训练示例中学习，每个训练示例都与一组候选标签相关联，其中只有一个子集对训练示例有效。诱导预测模型的常用策略是尝试消除候选标签集的歧义，例如通过利用每个候选标签的置信度来识别真实标签或估计候选标签集中的噪声标签。尽管如此，这些策略忽略了考虑与每个实例对应的基本标签分布，因为标签分布在训练集中没有明确可用。在本文中，提出了一种名为 PML-LD 的新的部分多标签学习策略，通过标签增强从部分多标签示例中学习。具体来说，通过利用特征空间的拓扑信息和标签之间的相关性来恢复标签分布。之后，通过将正则化多输出回归器与恢复的标签分布拟合来学习多类预测模型。合成数据集和真实数据集的实验结果清楚地验证了 PMLLD 解决 PML 问题的有效性。

一 介绍

        部分多标签学习处理每个训练示例与一组候选标签相关联的问题，其中只有一个子集对应于groundtruth标签。近年来，从具有部分多标签的数据中学习的需求自然出现在许多实际应用中（Zhou 2018；Xie and Huang 2018）。例如，在在线对象注释中（图 1），由于潜在的不可靠注释器，注释器给出的候选标签中只有一部分是有效的。部分多标签学习旨在从 PML 训练示例中引入多标签分类器，该分类器可以为未见过的实例分配一组适当的标签。

        直观地说，处理 PML 问题的基本策略是消歧，即从候选标签集中识别真实标签。最近的一项尝试是利用每个候选标签作为真实标签的置信度（Xie and Huang 2018）。尽管如此，置信度分数很容易出错，尤其是在假阳性标签比例很高的情况下，因为它忽略了非候选标签的不相关性。采用低秩假设来识别噪声标签以进行消歧（Yu et al. 2018; Sun et al. 2019）。对于可靠的标签提取技术，从候选标签集中识别出真实标签，以对未见过的实例进行最终预测（Fang 和 Zhang 2019）。

        为了处理部分多标签学习中的歧义，我们可以明确地为每个标签分配一个描述度，而不是去歧义。所有标签的描述度 构成一个实值向量，称为标签分布（Geng 2016），它描述了实例比逻辑标签更全面。这里 ∈ [0, 1] 和 = 1。请注意，在部分多标签学习问题中，标签分布比逻辑标签更重要，因为标签与实例的相关性或不相关性主要在三个方面是相对的：

                        图 2：关于 PML 中候选标签和非候选标签之间区别的示例

1、候选标签和非候选标签之间的区别是相对的。在部分多标签学习中，相关标签和不相关标签之间的界限并不清晰，这可能会导致分区将一些不相关的标签分配到候选标签集中。例如，在面部表情注释中（图 2），面部表情通常传达基本情绪的复杂混合（Zhou, Xue, and Geng 2015）。由不可靠的注释器选择的阈值导致候选标签集（例如，悲伤、惊讶、愤怒、厌恶和恐惧），其中惊喜无效。

2、候选标签之间的相关性是不同的，而不是完全相等的。例如，一张自然场景图像可能会同时使用候选标签天空、水、建筑物和云进行标注，但每个标签与该图像的相关性是不同的。

3、每个非候选标签的不相关性可能非常不同。例如，对于汽车，标签飞机比标签罐更无关紧要。

        尽管标签分布在部分多标签训练集中没有明确可用，但可以通过某种方式从训练集中恢复，这是一个名为标签增强的过程（Xu、Tao 和 Geng 2018）。因此，本文提出了一种新的局部多标签学习算法PML-LD，即Partial Multi-label Learning with Label Distribution。 PML-LD 通过利用特征空间的拓扑信息和标签之间的相关性来恢复标签分布。之后，通过将正则化多输出回归器与恢复的标签分布拟合来学习多类预测模型。

        本文的其余部分安排如下。首先，简要回顾了部分多标签学习的相关工作。其次，介绍了该方法的技术细节。第三，报告了比较实验的结果。最后，我们总结了这篇论文。

相关工作

        部分多标签学习与两个流行的学习框架密切相关，即多标签学习（Zhang 和 Zhou 2014；Gibaja 和 V entura 2015；Zhou 和 Zhang 2017）和部分标签学习（Cour、Sapp 和 Taskar 2011；Liu和 Dietterich 2012；张、宇和唐 2017）。

        在多标签学习 (MLL) 中，每个示例同时与多个有效标签相关联。基于用于模型训练的标签相关性顺序（Zhang and Zhou 2014），多标签学习方法可以大致分为三种类型。最简单的是一阶类型，它将问题分解为一系列二元分类问题，每个问题对应一个标签（Boutell et al. 2004; Zhang and Zhou 2007）。一阶方法忽略了一个标签的信息可能有助于学习另一个标签的事实。二阶方法考虑类标签对之间的相关性（Elisseeff 和 Weston 2002；Fürnkranz 等人 2008）。但是诸如 CLR (Fürnkranz et al. 2008) 和 RankSVM (Elisseeff and Weston 2002) 等二阶方法只关注相关标签和不相关标签之间的差异。高阶方法考虑标签子集或所有类标签之间的相关性（Read et al. 2011; Tsoumakas, Katakis, and Vlahavas 2011）。 MLL 和 PML 都旨在诱导预测模型，该模型可以为看不见的实例分配适当的标签集。尽管如此，PML 的任务比 MLL 更具挑战性，因为 PML 学习算法不能直接访问 ground-truth。        

        在部分标签学习（PLL）中，每个示例都与多个候选标签相关联，其中只有一个是有效的。部分标签学习的任务是引入一个多类预测模型，该模型可以为看不见的实例分配一个适当的标签，其中现有的 PLL 方法通过消除候选标签集的歧义（Cour、Sapp 和 Taskar 2011；Yu 和 Zhang 2017）或转换部分标签学习问题转化为典型的监督学习问题（Zhang, Yu, and Tang 2017）。 PLL 和 PML 都从带有标签噪声的训练示例中学习，其中假阳性标签驻留在候选标签集中。尽管如此，PML 的任务比 PLL 更具挑战性，因为需要从 PML 训练示例中引入多标签预测器而不是单标签预测器。

        为了解决部分多标签学习问题，处理 PML 问题的基本策略是消歧，即从候选标签集中识别真实标签。最近的一项尝试是利用每个候选标签作为真实标签的置信度（Xie and Huang 2018）。尽管如此，置信度分数很容易出错，尤其是在假阳性标签比例很高的情况下，因为它忽略了非候选标签的不相关性。采用低秩假设来识别噪声标签以进行消歧（Yu et al. 2018; Sun et al. 2019）。对于可靠的标签提取技术，从候选标签集中识别出真实标签，以对未见过的实例进行最终预测（Fang 和 Zhang 2019）。

        在下一节中，将介绍一种新颖的部分多标签学习方法。与现有的部分多标签学习方法不同，标签分布被恢复并用于促进学习过程。

提出方法

        标签分布估计

   表示c维的逻辑向量

表示候选标签集

 L表示逻辑标签矩阵

 标签分布矩阵来自逻辑标签矩阵L

PML—LDj假定参数模型

  一个权重矩阵和是一个基向量

 是一个非线性变换对x到更高维的特征空间

是集合

我们方法的目标是确定最优模型 ^W ∗ 最小化

 L是一个损失函数，是利用特征空间的拓扑信息的函数，Z是利用标签之间相关性的功能

 把公式（2)定义为最小二乘（LS）损失函数

 

         局部标签相关性 (Tsoumakas et al. 2009) 被认为可以提供有用的额外信息来从多标签中恢复标签分布。具体来说，两个标签的相关性越高，对应的描述度就应该越接近。换句话说，如果第 i 个和第 j 个标签更相关，则 di 应该更类似于 dj。这里di是第i个标签的所有描述度构成的向量

 是对应于所有实例的标签分布，是表示实例的高维特征的特征矩阵

 

 根据平滑假设（Zhu、Lafferty 和 Rosenfeld 2005），彼此靠近的点更有可能共享一个标签。直观地说，如果 xi 和 xj 具有高度相似性，用 aij 表示，那么 di 和 dj 应该彼此接近。因此，可以通过利用特征空间的拓扑信息（Ning, An, and Xin 2018）从训练示例中挖掘隐藏标签分布，这导致方程中的以下函数 Ω( ^W )。 (2):

    其中局部相似度矩阵 A 中的每个元素 aij 可以由下式计算     

 如果 xi 在 xj 的 K-最近邻中，否则 aij = 0。这里 K 设置为 c + 1。 G = ^A - A 是图拉普拉斯算子，^A 是其元素 ar 的对角矩阵

 

   将标签增强问题公式化为方程式上的优化框架。 (3)，等式。 (5) 和等式。 (4)，得到如下优化问题：              

 

 Predictive Model Induction

        在标签分布恢复的第一阶段之后，原始 PML 训练集 D 已转换为其基本对应物：E = {(xi, di)|1 ≤ i ≤ n}。在第二阶段，PML-LD 旨在基于 E 诱导出预测模型 f : X ?→ Y。考虑到 E 中每个训练样例的 di 实际上都是实值的，因此很自然地采用多-输出回归技术。与 MSVR 类似（Chung et al. 2015; Sánchez-Fernández et al. 2004），我们推广回归器来解决多维情况。然后，PML-LD 通过最小化以下损失函数来诱导回归模型：

         

 

 

结论

        在本文中，研究了 PML 的问题，提出了一种新的方法 PML-LD。与现有策略不同，PML-LD 考虑了训练数据集中的标签分布。由于训练集中没有明确的标签分布，PML-LD通过利用特征空间的拓扑信息和标签之间的相关性来恢复标签分布，然后基于多输出回归分析得出预测模型。通过对合成数据集和真实世界 PML 数据集的综合实验验证了所提出方法的有效性。