机器学习的概率统计模型(附代码)(二)
目录
数理统计
2.1 抽样分布
1)卡方()分布
2)t分布
3)F分布
2.2 大数定律
2.3中心极限定理
总结
系列文章目录
数理统计
数理统计是数学的一个分支,分为描述统计和推断统计。它以概率论为基础,研究大量随机现象的统计规律性。描述统计的任务是搜集资料,进行整理、分组,编制次数分配表,绘制次数分配曲线,计算各种特征指标,以描述资料分布的集中趋势、离中趋势和次数分布的偏斜度等。推断统计是在描述统计的基础上,根据样本资料归纳出的规律性,对总体进行推断和预测。
由于本文章会多次运用到matplotlib库的知识,如有需要请移步前往matplotlib库巩固知识点。
2.1 抽样分布
1)卡方(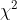 )分布
)分布
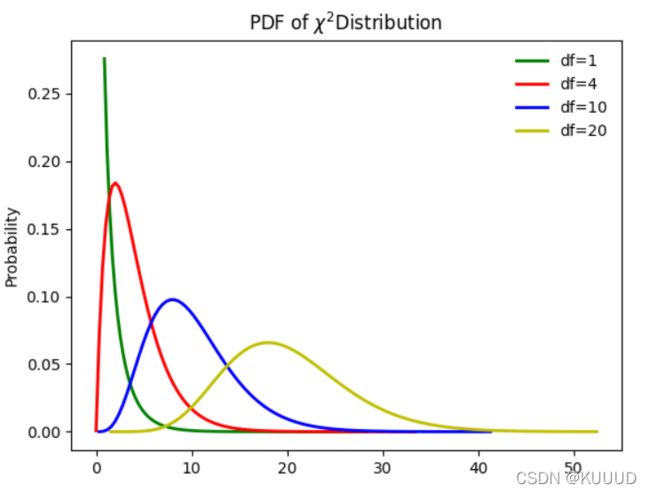
若n个相互独立的随机变量ξ₁,ξ₂,...,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
def diff_chi2_dis():
'''
不同参数下的卡方分布
:return:
'''
chi2_dis_0_5 = stats.chi2(df = 0.5)
chi2_dis_1 = stats.chi2(df = 1)
chi2_dis_4 = stats.chi2(df = 4)
chi2_dis_10 = stats.chi2(df = 10)
chi2_dis_20 = stats.chi2(df = 20)
#x1 = np.linspace(chi2_dis_0_5.ppf(0.01), chi2_dis_0_5.ppf(0.99), 100)
x2 = np.linspace(chi2_dis_1.ppf(0.65), chi2_dis_1.ppf(0.9999999), 100)
x3 = np.linspace(chi2_dis_4.ppf(0.000001), chi2_dis_4.ppf(0.999999), 100)
x4 = np.linspace(chi2_dis_10.ppf(0.000001), chi2_dis_10.ppf(0.99999), 100)
x5 = np.linspace(chi2_dis_20.ppf(0.00000001), chi2_dis_20.ppf(0.9999), 100)
fig, ax = plt.subplots(1,1)
#ax.plot(x1, chi2_dis_0_5.pdf(x1), 'k-', lw=2, label= 'df=0.5')
ax.plot(x2, chi2_dis_1.pdf(x2), 'g-', lw=2, label= 'df=1')
ax.plot(x3, chi2_dis_4.pdf(x3), 'r-', lw=2, label= 'df=4')
ax.plot(x4, chi2_dis_10.pdf(x4), 'b-', lw=2, label= 'df=10')
ax.plot(x5, chi2_dis_20.pdf(x5), 'y-', lw=2, label= 'df=20')
plt.ylabel('Probability')
plt.title(r'PDF of $\chi^2$Distribution')
ax.legend(loc='best', frameon=False)
plt.show()
diff_chi2_dis()当自由度df等于1或2时,函数图像都呈单调递减的趋;当df大于或等于3时,呈先增后减的趋势。从定义上来看,df的值只能取正整数。
2)t分布
t-分布用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
def diff_t_dis():
'''
不同参数下的卡方分布
:return:
'''
norm_dis = stats.norm()
t_dis_1 = stats.t(df = 1)
t_dis_4 = stats.t(df = 4)
t_dis_10 = stats.t(df = 10)
t_dis_20 = stats.t(df = 20)
x1 = np.linspace(norm_dis.ppf(0.000001), norm_dis.ppf(0.999999), 1000)
x2 = np.linspace(t_dis_1.ppf(0.04), t_dis_1.ppf(0.96), 1000)
x3 = np.linspace(t_dis_4.ppf(0.001), t_dis_4.ppf(0.999), 1000)
x4 = np.linspace(t_dis_10.ppf(0.001), t_dis_10.ppf(0.999), 1000)
x5 = np.linspace(t_dis_20.ppf(0.0001), t_dis_20.ppf(0.999), 1000)
fig, ax = plt.subplots(1,1)
ax.plot(x1, norm_dis.pdf(x1), 'k-', lw=2, label= r'N(0,1)')
ax.plot(x2, t_dis_1.pdf(x2), 'g-', lw=2, label= 'df=1')
ax.plot(x3, t_dis_4.pdf(x3), 'r-', lw=2, label= 'df=4')
ax.plot(x4, t_dis_10.pdf(x4), 'b-', lw=2, label= 'df=10')
ax.plot(x5, t_dis_20.pdf(x5), 'y-', lw=2, label= 'df=20')
plt.ylabel('Probability')
plt.title(r'PDF of t Distribution')
ax.legend(loc='best', frameon=False)
plt.show()
diff_t_dis()从上图可以看出,t分布和标准正态分布之间的差别还是比较大的,但当自由度n趋近于无穷大时,t分布与标准正态分布没有区别(推导后的公式也将变得完全一样);而当自由度n较小时,t分布比标准正态分布的尾部更宽,因此也比正态分布更慢地趋近于0。
3)F分布
F分布是两个服从卡方分布的独立随机变量各除以其自由度后的比值的抽样分布,是一种非对称分布,且位置不可互换。F分布有着广泛的应用,如在方差分析、回归方程的显著性检验中都有着重要的地位。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
def diff_F_dis():
'''
不同参数下的卡方分布
:return:
'''
#F_dis_0_5 = stats.F(dfn = 10, dfd = 1)
F_dis_1_30 = stats.f(dfn = 1, dfd = 30)
F_dis_30_5 = stats.f(dfn = 30, dfd = 5)
F_dis_30_30 = stats.f(dfn = 30, dfd = 30)
F_dis_30_100 = stats.f(dfn = 30, dfd = 100)
F_dis_10_100 = stats.f(dfn = 100, dfd = 100)
#x1 = np.linspace(F_dis_0_5.ppf(0.01), F_dis_0_5.ppf(0.99), 100)
x2 = np.linspace(F_dis_1_30.ppf(0.65), F_dis_1_30.ppf(0.99), 100)
x3 = np.linspace(F_dis_30_5.ppf(0.00001), F_dis_30_5.ppf(0.999), 100)
x4 = np.linspace(F_dis_30_30.ppf(0.00001), F_dis_30_30.ppf(0.999), 100)
x5 = np.linspace(F_dis_30_100.ppf(0.0001), F_dis_30_100.ppf(0.999), 100)
x6 = np.linspace(F_dis_10_100.ppf(0.0001), F_dis_10_100.ppf(0.9999), 100)
fig, ax = plt.subplots(1,1,figsize=(20,10))
#ax.plot(x1, F_dis_0_5.pdf(x1), 'k-', lw=2, label= 'F(0.5,0.5)')
ax.plot(x2, F_dis_1_30.pdf(x2), 'g-', lw=2, label= 'F(1,30)')
ax.plot(x3, F_dis_30_5.pdf(x3), 'r-', lw=2, label= 'F(30,5)')
ax.plot(x4, F_dis_30_30.pdf(x4), 'b-', lw=2, label= 'F(30,30)')
ax.plot(x5, F_dis_30_100.pdf(x5), 'y-', lw=2, label= 'F(30,100)')
ax.plot(x6, F_dis_10_100.pdf(x6), 'y-', lw=2, label= 'F(100,100)')
plt.ylabel('Probability')
plt.title(r'PDF of F Distribution')
ax.legend(loc='best', frameon=False)
plt.show()
diff_F_dis()2.2 大数定律
在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律。通俗地说,这个定理就是,在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。偶然中包含着某种必然。
2.3中心极限定理
中心极限定理,是指概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量近似服从正态分布的条件。它是概率论中最重要的一类定理,有广泛的实际应用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。
总结
本文为大家重点介绍了与人工智能有关的梳理统计方法,概率统计知识在人工智能领域发挥着非常重要的作用,如深度学习理论,概率图模型等都依赖于概率分布作为框架的基本建模语言,学习了解机器学习的概率统计对你的掌握百利无一害~~
欢迎大家留言一起讨论问题~~~
系列文章目录
第一章:机器学习的概率统计模型(附代码)(一)
第二章:机器学习的概率统计模型(附代码)(二)