- 数字孪生技术为UI前端注入新活力:实现产品设计的沉浸式体验
ui设计前端开发老司机
ui
hello宝子们...我们是艾斯视觉擅长ui设计、前端开发、数字孪生、大数据、三维建模、三维动画10年+经验!希望我的分享能帮助到您!如需帮助可以评论关注私信我们一起探讨!致敬感谢感恩!一、引言:从“平面交互”到“沉浸体验”的UI革命当用户在电商APP中翻看3D家具模型却无法感知其与自家客厅的匹配度,当设计师在2D屏幕上绘制汽车内饰却难以预判实际乘坐体验——传统UI设计的“平面化、静态化、割裂感”
- matlab卷积矩阵绝对值,MATLAB矩阵分析和计算
weixin_39928736
matlab卷积矩阵绝对值
MATLAB矩阵分析和计算编辑锁定讨论上传视频本词条缺少概述图,补充相关内容使词条更完整,还能快速升级,赶紧来编辑吧!《MATLAB矩阵分析和计算》是清华大学出版社出版的一本图书。[1]书名MATLAB矩阵分析和计算作者杜树春出版社清华大学出版社出版时间2019年6月1日定价59元ISBN9787302524816印次1-1印刷日期2019.04.23MATLAB矩阵分析和计算图书内容编辑本书侧重
- 提升企业级数据处理效率!TDengine 四个集群优化点详解
TDengine (老段)
TDengine运维大数据数据库物联网时序数据库服务器运维tdengine
为了帮助企业更好地进行大数据处理,我们在此前TDengine3.x系列版本中进行了几项与集群相关的优化和新功能开发,以提升集群的稳定性和在异常情况下的恢复能力。这些优化包括clusterID隔离、leaderrebalance、raftlearner和restorednode。本文将对这几项重要优化进行详细阐述,以解答企业在此领域的疑问,并帮助大家更好地应对相关挑战。clusterID隔离问题fi
- 中国银联豪掷1亿采购海光C86架构服务器
信创新态势
海光芯片C86国产芯片海光信息
近日,中国银联国产服务器采购大单正式敲定,基于海光C86架构的服务器产品中标,项目金额超过1亿元。接下来,C86服务器将用于支撑中国银联的虚拟化、大数据、人工智能、研发测试等技术场景,进一步提升其业务处理能力、用户服务效率和信息安全水平。作为我国重要的银行卡组织和金融基础设施,中国银联在全球183个国家和地区设有银联受理网络,境内外成员机构超过2600家,是世界三大银行卡品牌之一。此次中国银联发力
- 全面探索Kafka:架构、应用与流处理
Kafka:企业级消息系统与流处理平台的深度解析ApacheKafka作为分布式流处理平台,广泛应用于大数据处理和实时分析领域。本文将基于其官方文档,详细探讨Kafka的核心功能、应用场景以及如何进行有效管理。背景简介Kafka作为高吞吐量的消息系统,支持企业级的发布-订阅模式。它能够处理大量实时数据,并支持高并发读写操作。本文将依据Kafka官方文档的内容,逐层深入,从入门到高级应用,帮助读者全
- Flink时间窗口详解
bxlj_jcj
Flinkflink大数据
一、引言在大数据流处理的领域中,Flink的时间窗口是一项极为关键的技术,想象一下,你要统计一个电商网站每小时的订单数量。由于订单数据是持续不断产生的,这就形成了一个无界数据流。如果没有时间窗口的概念,你就需要处理无穷无尽的数据,难以进行有效的统计分析。而时间窗口的作用,就是将这无界的数据流按照时间维度切割成一个个有限的“数据块”,方便我们对这些数据进行处理和分析。比如,我们可以定义一个1小时的时
- 探索实时流处理的未来:Kafka Streams 深度指南
秋或依
探索实时流处理的未来:KafkaStreams深度指南项目介绍欢迎进入KafkaStreams:实时流处理的世界!这不仅仅是一本书,更是一个通往流处理领域深层奥秘的门户。由PrashantPandey编著,这本书以ApacheKafka2.1中的KafkaStreams库为核心,为读者铺就了一条从理解基础概念到熟练掌握KafkaStreams编程的路径。无论是软件工程师、数据架构师,还是对大数据处
- Elasticsearch搜索引擎存储:从原理到实践的全景解析
Python×CATIA工业智造
搜索引擎elasticsearch大数据
引言在大数据时代,数据规模呈指数级增长,传统数据库的模糊查询、实时分析能力逐渐成为瓶颈。Elasticsearch(简称ES)凭借其分布式架构、实时搜索和灵活的数据分析能力,成为企业级搜索与存储的核心引擎。截至2025年,ES在全球日志分析、电商搜索、实时监控等场景的市场占有率超过60%。本文将从存储架构、核心技术、应用场景及优化策略四个维度,深入解析Elasticsearch的设计哲学与实践价值
- Matlab裁剪降水数据:1km掩膜制作实战
咋(za)说
matlab降水数据处理裁剪掩膜制作降水数据裁剪China_Pre
1km降水数据处理-制作数据裁剪掩膜1.数据概述2掩膜文件制作示例2.1数据准备2.2matlab掩膜制作示例代码3结语 中国1km分辨率逐月降水量数据集(1901-2024)是高精度、长时间序列的气候数据产品,广泛应用于水文、生态、农业等领域的研究。本篇基于应用需要,以该数据集为输入,结合研究区shp边界文件,制作用于数据提取/裁剪的掩膜文件。下面为具体内容。1.数据概述 中国1km分辨率逐
- 【Kafka专栏 13】Kafka的消息确认机制:不是所有的“收到”都叫“确认”!
作者名称:夏之以寒作者简介:专注于Java和大数据领域,致力于探索技术的边界,分享前沿的实践和洞见文章专栏:夏之以寒-kafka专栏专栏介绍:本专栏旨在以浅显易懂的方式介绍Kafka的基本概念、核心组件和使用场景,一步步构建起消息队列和流处理的知识体系,无论是对分布式系统感兴趣,还是准备在大数据领域迈出第一步,本专栏都提供所需的一切资源、指导,以及相关面试题,立刻免费订阅,开启Kafka学习之旅!
- MATLAB实现快速非局部均值图像去噪方法
一只爪子
本文还有配套的精品资源,点击获取简介:非局部均值滤波是一种先进的图像去噪技术,与传统方法相比,它利用图像的全局信息来去除噪声,同时保持图像细节。该算法通过搜索和利用整个图像中相似的像素块,对每个像素点进行去噪处理。本文提供的MATLAB代码FAST_NLM_II.m实现此算法,并包含必要的参数设置、相似性计算、加权平均和图像更新步骤。了解并应用此代码是学习和进一步改进非局部均值滤波技术的基础。1.
- C语言学生成绩管理系统<;自创>;(功能7有小错误,但可运行)
han_xue_feng
java
腾讯云加速企业和个人开发创新公开直播预告直播预告:07/18(周四)15:00-16:00随着人工智能与大模型的蓬勃发展,我们正步入一个由技微信实习第一天周五入职,早上早早来到了公司,发现好多人都没上班,到十点才陆陆续续有人来,办理完入职后,mentor中联夏令营遗憾没有入选不过hr的回复真的很好,辛苦啦#提前批简历挂麻了怎么办##机械制造投递记录#大数据开发的工作有点过于简单了吧sq大数据开发的
- Python爬虫:从图片或扫描文档中提取文字数据的完整指南
Python爬虫项目
2025年爬虫实战项目python爬虫开发语言数据挖掘c++
1.引言随着大数据技术的不断进步,图像数据逐渐成为了许多行业中重要的数据源之一。图像中不仅包含了丰富的视觉信息,还可能蕴含着大量的文字数据。对于科研、企业、政府等多个领域而言,如何从图片或扫描文档中提取出有价值的文字信息是一个亟待解决的问题。在这一过程中,OCR(OpticalCharacterRecognition,光学字符识别)技术成为了解决这一问题的重要工具。在本文中,我们将探讨如何使用Py
- 【C语言经典面试题】memcpy函数有没有更高效的拷贝实现方法?
架构师李肯
嵌入式物联网开发进阶c语言面试性能优化
【C语言经典面试题】memcpy函数有没有更高效的拷贝实现方法?我相信大部分初中级C程序员在面试的过程中,可能都被问过关于memcpy函数的问题,甚至需要手撕memcpy。本文从另一个角度带你领悟一下memcpy的面试题,你可以看看是否能接得住?文章目录1写在前面2源码实现2.1函数申明2.2简单的功能实现2.3满足大数据量拷贝的功能实现3源码测试4小小总结5更多分享1写在前面假如你遇到下面的面试
- python基于Hadoop的NBA球员大数据分析与可视化系统
目录技术栈介绍具体实现截图系统设计研究方法:设计步骤设计流程核心代码部分展示研究方法详细视频演示试验方案论文大纲源码获取/详细视频演示技术栈介绍Django-SpringBoot-php-Node.js-flask本课题的研究方法和研究步骤基本合理,难度适中,本选题是学生所学专业知识的延续,符合学生专业发展方向,对于提高学生的基本知识和技能以及钻研能力有益。该学生能够在预定时间内完成该课题的设计。
- 大数据技术之集群数据迁移
dfs.namenode.rpc-address.nameservice1.namenode30hadoop104:8020dfs.namenode.rpc-address.nameservice1.namenode37hadoop106:8020dfs.namenode.http-address.nameservice1.namenode30hadoop104:9870dfs.namenode.
- 如何通过YashanDB优化企业大数据处理流程
数据库
在当今数据驱动的商业环境中,企业面临着巨大的数据处理挑战。性能瓶颈、数据一致性问题和可扩展性需求使得大数据处理成为一项复杂任务。作为一种新兴的数据库管理系统,YashanDB以其独特的架构设计和强大的数据处理能力,在解决这些挑战方面提供了有效的手段。本文旨在探讨如何利用YashanDB优化大数据处理流程,为企业提供高效、可靠的解决方案。YashanDB的体系架构与部署形态YashanDB支持多种部
- matlab画信号图方法,献给初学者:手把手教你绘制信号通路图
信号通路是指能将细胞外的分子信号经细胞膜传入细胞内发挥效应的一系列酶促反应通路。细胞信号通路图是科研研究过程中最常见也是最常用到的,如何绘制适合我们自己科研课题的信号通路图呢?可以试试pathwaybuildertool软件。这款软件简单易学,即便是零基础的同学,也可以做出漂亮的信号通路。1.首先,打开PathwayBuilderTool2.0软件,软件自带分子生物学会用到的基本元素,如不同的细胞
- Pandas 学习教程
_pass_
Data-Alaysispandas信息可视化
目录定义基本操作一维数组操作二维数组操作数据选择过滤数据处理数据清洗数据转换数据分析排序分组聚合数据透视表高级操作合并数据时间序列处理自定义函数调用数据可视化集成数据导出和导入大数据分块处理定义全称:'paneldata'and'pythondataanalysis'Analy:Series(一维数据)、DataFrame(二维数据)主要应用:数据清洗:处理缺失数据、重复数据等数据转换:改变数据的
- 如何通过YashanDB提升客户体验
数据库
如何优化查询速度?这是许多企业在使用数据库技术时常常会遇到的问题。查询速度的快慢直接影响到用户的体验,尤其是在大数据量和高并发的使用场景中。顾客期望迅速获取信息,若响应时间过长,可能导致客户流失。因此,优化数据库的性能成为提升客户体验的关键举措之一。YashanDB作为一种高性能的数据库技术架构,提供了多种优化机制,以提升系统的查询速度和整体处理能力。多种部署架构YashanDB支持多种部署架构,
- 如何通过YashanDB数据库实现企业级数据分区管理?
数据库
在当今大数据时代,企业面临着海量数据的管理和优化访问的问题。如何有效地组织和划分庞大的数据集,以提升查询性能和运维效率,成为数据库系统设计的核心挑战。数据分区技术作为解决大规模数据处理的关键手段,能够显著减少无关数据的访问,优化资源利用率。本文聚焦于YashanDB数据库,详细解析其数据分区管理的实现机制及应用,为企业级应用提供高效、灵活的数据分区解决方案。YashanDB中的数据分区基础Yash
- 国产开源高性能对象存储RustFS保姆级上手指南
光爷不秃
对象存储rust国产开源软件rust云计算开源软件github开源数据仓库database
在云计算与大数据爆发的时代,企业和开发者对存储方案的要求愈发严苛——不仅要能扛住海量数据的读写压力,还得兼顾安全性、可扩展性和兼容性。今天给大家介绍一款基于Rust语言开发的开源分布式对象存储系统——RustFS,它不仅是MinIO的国产化优秀替代方案,更是AI、大数据和云原生场景的理想之选。本文将从基础介绍到实战操作,带大家快速上手这款"优雅的存储解决方案"。一、RustFS核心特性解析Rust
- 【论文复现】Taylor算法用于TOA(到达时间)的三维标签位置解算,360个标签、12个基站的环境作为验证,附MATLAB例程
MATLAB卡尔曼
论文复现算法matlab开发语言
本文给出论文《基于Taylor-Chan算法的改进UWB室内三维定位方法》中的Taylor算法来解算TOA的复现程序(MATLAB)。使用论文中给定的12个锚点/360个测试的标签用来测试算法性能文章目录运行结果程序介绍核心功能概述结果输出应用场景MATLAB源代码运行结果误差输出:程序介绍本程序基于Taylor迭代算法,实现了对三维空间内360个目标点的TOA(TimeofArrival)定位解
- 通过YashanDB提升大数据处理能力的指南
数据库
数据的急剧增长给数据库技术领域带来了诸多挑战,包括性能瓶颈、数据一致性问题及处理效率低下等。为了应对这些挑战,企业需采取有效的技术手段来提升大数据处理能力。YashanDB作为一款高性能的数据库产品,通过其先进的体系架构、优化的数据存储形式以及强大的并发控制能力,有效地提升了大数据环境下的处理性能。本文旨在为技术人员和决策者提供深入的技术分析和可操作的建议,通过YashanDB的功能特性来实现大数
- matlab计算转子系统的固有频率、振型、不平衡响应
可以计算转子系统的固有频率、振型、不平衡响应MatrixRiccati/code/Dichotomy_1(2).m,2210MatrixRiccati/code/Dichotomy_1.m,2210MatrixRiccati/code/RiccatiSY_1.m,2756MatrixRiccati/code/Trans1x(2).m,451MatrixRiccati/code/Trans1x.m,
- 基于MATLAB的语音信号预处理
3.1.语音信号的预加重处理对语音的的高频部分进行加重以去除口唇部分的影响,就必须要对输入的数字语音信号进行预加重处理,以此来增加语音的高频分辨率。通常通过传递函数为的一阶FIR高通数字滤波器来实现预加重,其中为预加重系数,0.9<<1.0。设n时刻的语音采样值为X(n),经过预加重处理的结果为,这里取=0.98。图3.1为该高通滤波器的幅频特性及相频特性。图3.2中分别给出了预加重前和预加重后的
- Java多线程实战指南:从基础到高并发的核心技术解析
添砖Java中
javapython开发语言springbootspringcloudspring
一、为什么必须掌握多线程?在单核CPU时代,多线程主要用于提高程序响应速度;在如今的多核处理器时代,多线程已成为榨干硬件性能的必备技能。无论是高并发Web服务器、实时数据处理系统,还是游戏引擎,都离不开多线程技术的支撑。典型案例:电商秒杀系统:1秒内处理10万+请求大数据处理:并行计算TB级数据金融交易系统:毫秒级订单撮合二、线程创建的四大核心方式1.继承Thread类(不推荐)classMyTh
- 3D 可视化技术开启污水治理全新发展阶段
广州华锐视点
3d
3D可视化大屏展示技术在污水厂的应用,已然开启了污水处理的全新篇章。它不仅为污水厂解决了当下管理和展示的难题,更如同一座灯塔,照亮了未来污水处理领域的发展道路。随着科技的持续进步,3D可视化大屏展示技术必将迎来更加辉煌的发展。一方面,其与人工智能、大数据、物联网等前沿技术的融合将愈发紧密。借助人工智能算法,大屏系统将具备更强大的自主学习和分析能力,能够根据实时数据和历史经验,自动优化污水处理工艺参
- UI前端大数据可视化实战策略:如何设计交互式数据探索界面?
UI前端开发工作室
ui前端信息可视化
hello宝子们...我们是艾斯视觉擅长ui设计、前端开发、数字孪生、大数据、三维建模、三维动画10年+经验!希望我的分享能帮助到您!如需帮助可以评论关注私信我们一起探讨!致敬感谢感恩!一、引言:从“被动观看”到“主动探索”的可视化革命传统大数据可视化常陷入“图表堆砌”的困境:企业dashboard上布满折线图、饼图,却难以回答“销售额下降的核心区域是哪里”“用户流失与哪个行为强相关”等深度问题。
- 【HTML网页】智能健康监测——全方位健康管理专家(包含网页源代码)
智能健康监测分析系统智能健康监测分析系统是一种基于物联网、大数据、人工智能等技术的综合性健康管理解决方案。它具有以下六大核心功能:实时监测系统通过智能传感器和可穿戴设备,实时采集用户的生理数据,例如心率、血压、血氧饱和度、血糖水平和睡眠质量等,确保用户随时掌握自己的身体状况。健康数据分析利用人工智能和大数据分析技术,系统对采集到的数据进行处理和分析,提取有价值的健康信息,如心率变异性、呼吸频率等,
- 关于旗正规则引擎下载页面需要弹窗保存到本地目录的问题
何必如此
jsp超链接文件下载窗口
生成下载页面是需要选择“录入提交页面”,生成之后默认的下载页面<a>标签超链接为:<a href="<%=root_stimage%>stimage/image.jsp?filename=<%=strfile234%>&attachname=<%=java.net.URLEncoder.encode(file234filesourc
- 【Spark九十八】Standalone Cluster Mode下的资源调度源代码分析
bit1129
cluster
在分析源代码之前,首先对Standalone Cluster Mode的资源调度有一个基本的认识:
首先,运行一个Application需要Driver进程和一组Executor进程。在Standalone Cluster Mode下,Driver和Executor都是在Master的监护下给Worker发消息创建(Driver进程和Executor进程都需要分配内存和CPU,这就需要Maste
- linux上独立安装部署spark
daizj
linux安装spark1.4部署
下面讲一下linux上安装spark,以 Standalone Mode 安装
1)首先安装JDK
下载JDK:jdk-7u79-linux-x64.tar.gz ,版本是1.7以上都行,解压 tar -zxvf jdk-7u79-linux-x64.tar.gz
然后配置 ~/.bashrc&nb
- Java 字节码之解析一
周凡杨
java字节码javap
一: Java 字节代码的组织形式
类文件 {
OxCAFEBABE ,小版本号,大版本号,常量池大小,常量池数组,访问控制标记,当前类信息,父类信息,实现的接口个数,实现的接口信息数组,域个数,域信息数组,方法个数,方法信息数组,属性个数,属性信息数组
}
&nbs
- java各种小工具代码
g21121
java
1.数组转换成List
import java.util.Arrays;
Arrays.asList(Object[] obj); 2.判断一个String型是否有值
import org.springframework.util.StringUtils;
if (StringUtils.hasText(str)) 3.判断一个List是否有值
import org.spring
- 加快FineReport报表设计的几个心得体会
老A不折腾
finereport
一、从远程服务器大批量取数进行表样设计时,最好按“列顺序”取一个“空的SQL语句”,这样可提高设计速度。否则每次设计时模板均要从远程读取数据,速度相当慢!!
二、找一个富文本编辑软件(如NOTEPAD+)编辑SQL语句,这样会很好地检查语法。有时候带参数较多检查语法复杂时,结合FineReport中生成的日志,再找一个第三方数据库访问软件(如PL/SQL)进行数据检索,可以很快定位语法错误。
- mysql linux启动与停止
墙头上一根草
如何启动/停止/重启MySQL一、启动方式1、使用 service 启动:service mysqld start2、使用 mysqld 脚本启动:/etc/inint.d/mysqld start3、使用 safe_mysqld 启动:safe_mysqld&二、停止1、使用 service 启动:service mysqld stop2、使用 mysqld 脚本启动:/etc/inin
- Spring中事务管理浅谈
aijuans
spring事务管理
Spring中事务管理浅谈
By Tony Jiang@2012-1-20 Spring中对事务的声明式管理
拿一个XML举例
[html]
view plain
copy
print
?
<?xml version="1.0" encoding="UTF-8"?>&nb
- php中隐形字符65279(utf-8的BOM头)问题
alxw4616
php中隐形字符65279(utf-8的BOM头)问题
今天遇到一个问题. php输出JSON 前端在解析时发生问题:parsererror.
调试:
1.仔细对比字符串发现字符串拼写正确.怀疑是 非打印字符的问题.
2.逐一将字符串还原为unicode编码. 发现在字符串头的位置出现了一个 65279的非打印字符.
- 调用对象是否需要传递对象(初学者一定要注意这个问题)
百合不是茶
对象的传递与调用技巧
类和对象的简单的复习,在做项目的过程中有时候不知道怎样来调用类创建的对象,简单的几个类可以看清楚,一般在项目中创建十几个类往往就不知道怎么来看
为了以后能够看清楚,现在来回顾一下类和对象的创建,对象的调用和传递(前面写过一篇)
类和对象的基础概念:
JAVA中万事万物都是类 类有字段(属性),方法,嵌套类和嵌套接
- JDK1.5 AtomicLong实例
bijian1013
javathreadjava多线程AtomicLong
JDK1.5 AtomicLong实例
类 AtomicLong
可以用原子方式更新的 long 值。有关原子变量属性的描述,请参阅 java.util.concurrent.atomic 包规范。AtomicLong 可用在应用程序中(如以原子方式增加的序列号),并且不能用于替换 Long。但是,此类确实扩展了 Number,允许那些处理基于数字类的工具和实用工具进行统一访问。
- 自定义的RPC的Java实现
bijian1013
javarpc
网上看到纯java实现的RPC,很不错。
RPC的全名Remote Process Call,即远程过程调用。使用RPC,可以像使用本地的程序一样使用远程服务器上的程序。下面是一个简单的RPC 调用实例,从中可以看到RPC如何
- 【RPC框架Hessian一】Hessian RPC Hello World
bit1129
Hello world
什么是Hessian
The Hessian binary web service protocol makes web services usable without requiring a large framework, and without learning yet another alphabet soup of protocols. Because it is a binary p
- 【Spark九十五】Spark Shell操作Spark SQL
bit1129
shell
在Spark Shell上,通过创建HiveContext可以直接进行Hive操作
1. 操作Hive中已存在的表
[hadoop@hadoop bin]$ ./spark-shell
Spark assembly has been built with Hive, including Datanucleus jars on classpath
Welcom
- F5 往header加入客户端的ip
ronin47
when HTTP_RESPONSE {if {[HTTP::is_redirect]}{ HTTP::header replace Location [string map {:port/ /} [HTTP::header value Location]]HTTP::header replace Lo
- java-61-在数组中,数字减去它右边(注意是右边)的数字得到一个数对之差. 求所有数对之差的最大值。例如在数组{2, 4, 1, 16, 7, 5,
bylijinnan
java
思路来自:
http://zhedahht.blog.163.com/blog/static/2541117420116135376632/
写了个java版的
public class GreatestLeftRightDiff {
/**
* Q61.在数组中,数字减去它右边(注意是右边)的数字得到一个数对之差。
* 求所有数对之差的最大值。例如在数组
- mongoDB 索引
开窍的石头
mongoDB索引
在这一节中我们讲讲在mongo中如何创建索引
得到当前查询的索引信息
db.user.find(_id:12).explain();
cursor: basicCoursor 指的是没有索引
&
- [硬件和系统]迎峰度夏
comsci
系统
从这几天的气温来看,今年夏天的高温天气可能会维持在一个比较长的时间内
所以,从现在开始准备渡过炎热的夏天。。。。
每间房屋要有一个落地电风扇,一个空调(空调的功率和房间的面积有密切的关系)
坐的,躺的地方要有凉垫,床上要有凉席
电脑的机箱
- 基于ThinkPHP开发的公司官网
cuiyadll
行业系统
后端基于ThinkPHP,前端基于jQuery和BootstrapCo.MZ 企业系统
轻量级企业网站管理系统
运行环境:PHP5.3+, MySQL5.0
系统预览
系统下载:http://www.tecmz.com
预览地址:http://co.tecmz.com
各种设备自适应
响应式的网站设计能够对用户产生友好度,并且对于
- Transaction and redelivery in JMS (JMS的事务和失败消息重发机制)
darrenzhu
jms事务承认MQacknowledge
JMS Message Delivery Reliability and Acknowledgement Patterns
http://wso2.com/library/articles/2013/01/jms-message-delivery-reliability-acknowledgement-patterns/
Transaction and redelivery in
- Centos添加硬盘完全教程
dcj3sjt126com
linuxcentoshardware
Linux的硬盘识别:
sda 表示第1块SCSI硬盘
hda 表示第1块IDE硬盘
scd0 表示第1个USB光驱
一般使用“fdisk -l”命
- yii2 restful web服务路由
dcj3sjt126com
PHPyii2
路由
随着资源和控制器类准备,您可以使用URL如 http://localhost/index.php?r=user/create访问资源,类似于你可以用正常的Web应用程序做法。
在实践中,你通常要用美观的URL并采取有优势的HTTP动词。 例如,请求POST /users意味着访问user/create动作。 这可以很容易地通过配置urlManager应用程序组件来完成 如下所示
- MongoDB查询(4)——游标和分页[八]
eksliang
mongodbMongoDB游标MongoDB深分页
转载请出自出处:http://eksliang.iteye.com/blog/2177567 一、游标
数据库使用游标返回find的执行结果。客户端对游标的实现通常能够对最终结果进行有效控制,从shell中定义一个游标非常简单,就是将查询结果分配给一个变量(用var声明的变量就是局部变量),便创建了一个游标,如下所示:
> var
- Activity的四种启动模式和onNewIntent()
gundumw100
android
Android中Activity启动模式详解
在Android中每个界面都是一个Activity,切换界面操作其实是多个不同Activity之间的实例化操作。在Android中Activity的启动模式决定了Activity的启动运行方式。
Android总Activity的启动模式分为四种:
Activity启动模式设置:
<acti
- 攻城狮送女友的CSS3生日蛋糕
ini
htmlWebhtml5csscss3
在线预览:http://keleyi.com/keleyi/phtml/html5/29.htm
代码如下:
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title>攻城狮送女友的CSS3生日蛋糕-柯乐义<
- 读源码学Servlet(1)GenericServlet 源码分析
jzinfo
tomcatWebservlet网络应用网络协议
Servlet API的核心就是javax.servlet.Servlet接口,所有的Servlet 类(抽象的或者自己写的)都必须实现这个接口。在Servlet接口中定义了5个方法,其中有3个方法是由Servlet 容器在Servlet的生命周期的不同阶段来调用的特定方法。
先看javax.servlet.servlet接口源码:
package
- JAVA进阶:VO(DTO)与PO(DAO)之间的转换
snoopy7713
javaVOHibernatepo
PO即 Persistence Object VO即 Value Object
VO和PO的主要区别在于: VO是独立的Java Object。 PO是由Hibernate纳入其实体容器(Entity Map)的对象,它代表了与数据库中某条记录对应的Hibernate实体,PO的变化在事务提交时将反应到实际数据库中。
实际上,这个VO被用作Data Transfer
- mongodb group by date 聚合查询日期 统计每天数据(信息量)
qiaolevip
每天进步一点点学习永无止境mongodb纵观千象
/* 1 */
{
"_id" : ObjectId("557ac1e2153c43c320393d9d"),
"msgType" : "text",
"sendTime" : ISODate("2015-06-12T11:26:26.000Z")
- java之18天 常用的类(一)
Luob.
MathDateSystemRuntimeRundom
System类
import java.util.Properties;
/**
* System:
* out:标准输出,默认是控制台
* in:标准输入,默认是键盘
*
* 描述系统的一些信息
* 获取系统的属性信息:Properties getProperties();
*
*
*
*/
public class Sy
- maven
wuai
maven
1、安装maven:解压缩、添加M2_HOME、添加环境变量path
2、创建maven_home文件夹,创建项目mvn_ch01,在其下面建立src、pom.xml,在src下面简历main、test、main下面建立java文件夹
3、编写类,在java文件夹下面依照类的包逐层创建文件夹,将此类放入最后一级文件夹
4、进入mvn_ch01
4.1、mvn compile ,执行后会在
![]()
![]() ,
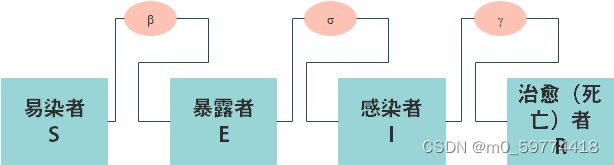
,![]() ,a.
,a.![]() ,
,![]() ,a分别为潜伏期自愈转化为康复者,即接触过感染者但未被感染,患病者治愈后转为康复者的概率,潜伏者对易感人群的传染率。
,a分别为潜伏期自愈转化为康复者,即接触过感染者但未被感染,患病者治愈后转为康复者的概率,潜伏者对易感人群的传染率。![]()
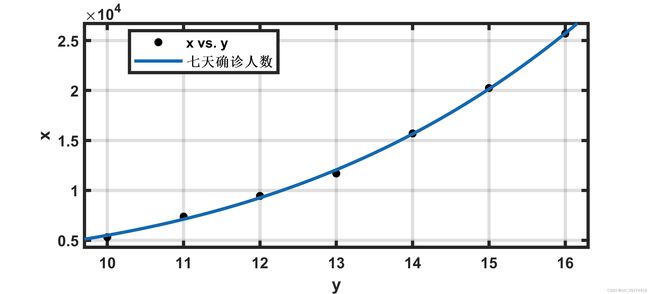
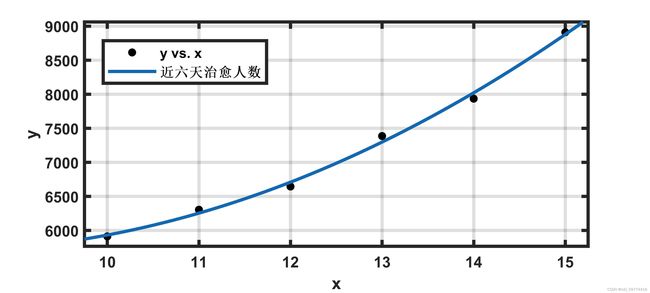
![]() 。查找近七天的数据,运用MATLAB拟合工具箱对数据进行拟合。
。查找近七天的数据,运用MATLAB拟合工具箱对数据进行拟合。![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()