基于SEIR的传播动力学模型

问题提出

问题1：请收集前期疫情发病数据，根据疫病传播过程中的实际情况，结合实际，建立一个真正能够预测以及能为预防和控制提供可靠、足够信息的传播模型；并且对于所采取的措施做出评论，如：提前或延后5天采取严格的隔离措施，对疫情传播所造成的影响做出估计。

问题2：请查阅相关资料，建立一个真正能够预测以及能为预防和控制提供可靠、足够的信息的传播模型，评价其合理性和实用性。

问题3：现在疾病已经在大范围内流行，请查找相关资料，建立一个对于世界的疫情传播模型，并评价模型的合理性和有效性。

问题4：收集疫情对经济某个方面影响的数据，建立相应的数学模型并进行预测。

模型假设

1.忽略超级传播者，病毒突变等等此类造成大规模传染的事件。
2.环境一个封闭空间，不考虑外来病例的输入。
3.官方发布的信息与防控措施无需时间延迟，即完成效率为100%。
4.人口在疫情发病期间不更新。
5.病毒在接触到人体有效感染部位就立即感染。
6.传播空间中人群均匀分布，不存在大型集会事件。
7.病人和潜伏期患者的使健康人患病的能力一致。
8.潜伏期的病人不被发现也不接受治疗。
9.每天治愈病患的人数在不受任何措施的影响下是一个定值。
10.生产技术条件不变。

名词定义与符号说明

4.1名词定义
1.减弱系数：采取疫情防控措施后，有效感染能力降低的比例参数。
2.有效感染能力：病人或者感染者接触健康人并成功使其转化为潜伏期患者的能力。
3.临界接种水平：人群获得免疫的临界平衡比例，(当达到此水平时，传染病才会逐渐停止传播。
4.2符号说明
表1：符号说明
符号 意义
I(t) 当前时刻病人所占总人数的比例函数
Q(t) 当前时刻潜伏期人数占总人数的比例函数
S(t) 当前时刻健康人所占总人数的比例函数
R(t) 当前时刻移出者所占总人数的比例函数
D(t) 当前时刻死亡人数所占总人数的比例函数
Q(t)t-i 当前t时刻的t-i时刻潜伏期人数占总人数的比例函数（滞后变量）
λ(t) 当前时刻有效个人感染函数
W(t) t时刻内移出者占总人数的比例
K(t) t时刻的资金函数
P(t) t时刻的产值函数
L(t) t时刻的劳动力函数
d 死亡率
μ 治愈率
t 时间变量
α 滞后变量的权数
i 单位变量
N 人口总数
c
K 减弱系数
每天治愈的人数
m
Vc 免疫系数
临界接种水平

模型的建立与求解

与传统的SEIR模型不同，处于潜伏期的病人具有传染能力，传染期的患者成为病人的期间有一个2-14天的爆发时间，由此我们引入了时间滞后变量，通过分布滞后模型的经验加权法得出Q(t)本身的时间分布。而实际情况中λ的并不是一共定值，因为病人，潜伏期患者，健康人和移出者是随时间的变化而不断变化的，λ(t)函数理应纳入到模型的建立之中，综合传统的SEIR模型，对之进行符合实际情况的改进，从而得出最终的病毒预测模型。根据实际情况，疫情的发展分为两个阶段，一是自由传播而不采取防控措施，二是防控阶段，具体如下。
5.1.1通过经验加权法对滞后变量权数的求解
根据病情发作的特点、实际的数据经验给各滞后变量指定权数，滞后变量通过权数进行线性组合最终得到新的变量。由题意得，病情的发作时间为2-14天，其中5.2天时为均值即发病较为集中，因此我们选取的权数据类型倒V型。定义13个滞后变量：〖Q(t)〗(t-2) 、〖Q(t)〗(t-3) 、〖Q(t)〗(t-4) 、…〖Q(t)〗(t-14)
以下是对Q(t)的线性函数定义：
Q(∆t)=∑_(i=2)^14▒〖α_i 〖Q(t)〗_(t-i) 〗

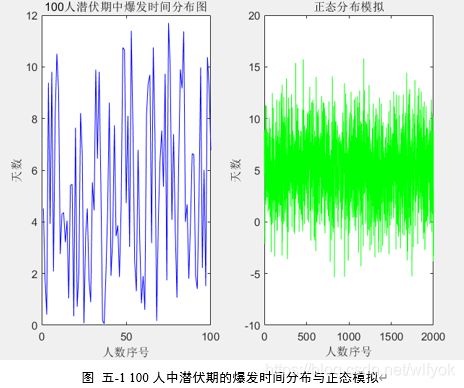
在大样本条件下，由中心极限定理知疫情在潜伏期内的发病分布服从正态分布，即有
lim┬(n→∞)⁡〖(|∑_(i=1)^n▒x_i -nE(x)|)=1〗。

图 五 1 100人中潜伏期的爆发时间分布与正态模拟
在大样本数据下（数据表格见附录）求得x ̅=5.2308，s=3.3439取定
α_i=∫_(i-0.5)^(i+0.5)▒〖1/√2Πσ e^(〖(x-u)〗2/(2σ^2 )) 〗
解得α_i的值分别为[0.09,0.11,0.13,0.13,0.13,0.12,0.10,0.07,0.05,0.03,0.02，0.01，0.005]。
5.1.2优化后的传染病模型的建立
模型一共把人群分为五大部分，分别为健康人、病人、潜伏期患者、移出者和死亡者。通过考虑潜伏期患者的潜伏期对于发病的时间滞后效应，与传播者有效感染函数和SEIR模型结合实际，通过对数据处理和适当假设下建立了疫情发展模型。

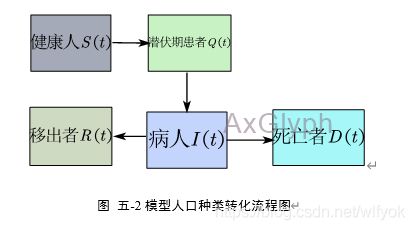
图 五 2模型人口种类转化流程图
经过计算化简得单位时间内病人的变化量是潜伏期患者的转化量减去病人的治愈数，则有
(dI(t))/dt=∑_(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗(t-i)-ui(t)〗-dI(t)
单位时间内潜伏期患者的变化量等于潜伏期患者转化为病人的减少量的负值加上单位时间内健康人被转化为潜伏期患者的数量，由微分方程定义得
(dQ(t))/dt=-∑(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗(t-i) 〗+λ(t)s(t)[I(t)+Q(t)]
健康人数的变化量为健康人转化为潜伏期患者的负值
(dS(t))/dt=-λ(t)s(t)[I(t)+Q(t)]
根据有效接触感染的定义得，其与健康人，病人，潜伏期患者均有关系，经推导有
(dλ(t))/dt=kλ(t)s(t)
而对于死亡者单位时间的变化量有
(dD(t))/dt=dI(t)
移出者所占比例为
(dR(t))/dt=μI(t)
经过时间推移，疫情的严重性引起了高度重视，采取了严格的防控措施。在第二阶段，病人的变化量为
(dI(t))/dt=Q(t)=∑(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗(t-i)-μi(t) 〗-dI(t)
防控期间，病人得到隔离不再具有传播病毒能力，同时潜伏期患者传播病毒的能力也大大减小，但不可忽视，故而引入减弱系数c，所以潜伏期患者的方程为
(dQ(t))/dt=-∑(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗_(t-i) 〗+cλ(t)s(t)Q(t)
相应地，由于病人不再传播病毒，健康人转化为潜伏期患者的关系变为
(dS(t))/dt=-cλ(t)s(t)Q(t)
不难推知，有效感染函数与死亡者函数的形式不变
(dλ(t))/dt=kλ(t)s(t)
(dD(t))/dt=dI(t)
此事，由于采取了一定的措施，加大了医疗强度，故使得每天治愈患者的人数得到提高，此时每天治愈患者的人数为μ_1，移出者所占比例的微分为为
(dR(t))/dt=μ_1 I(t)
5.1.2模型的求解
设定初值为[0.0000575 0 0.9999525 15 0.0217],分别对应病人，潜伏期患者，健康人，有效传染指数和死亡率，用Matlab编写程序求解得

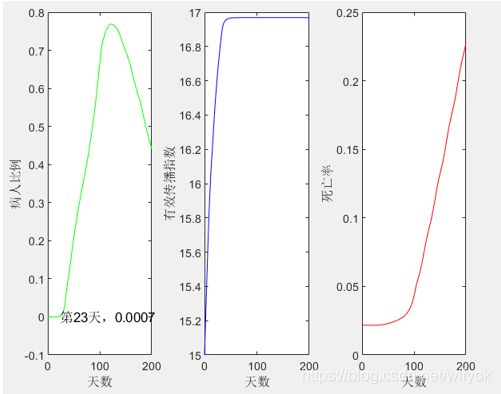
图 五 3病人比例、有效感染指数与死亡率趋势图(如为未采取防控措施)
当采取措施后，取定病人比例的初值为0.0007，带入采取措施后的模型中计算画图得

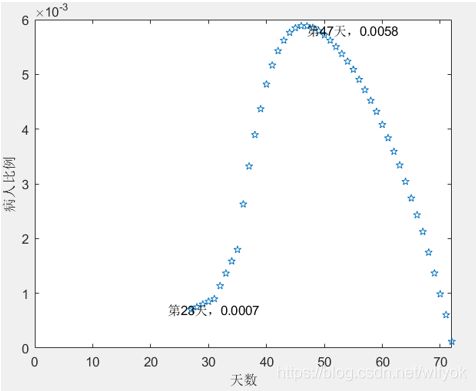
图 五 4 发病第23天采取防控措施后病人比例趋势图

政策——“群体免疫”。在治愈率较低以及防控措施不到位的情况下，采用适应实际情况的优化后的微分方程模型对其进行趋势预测。
5.3.1数据处理
根据预测截至到3.24日的数据(见附录),对数据进行可视化处理

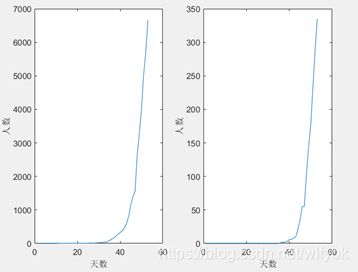
图 五 6 确诊人数与死亡人数的时间分布图
5.3.2病毒传播模型的动态模拟
在治愈率相对较低与防控措施不齐全的前提下，通过Matlab对病情的传播进行了模拟。

图 五 7病毒传播动态模拟图(1)

病情初始，病毒在人群中爆炸式扩散，大部分人群被病毒感染。

图 五 8病毒传播动态模拟图(2)

随着时间推移，移出者逐渐出现，最后形成“群体免疫”，渡过这次疫情。显然，这是要付出沉重代价的。
5.3.3模型的建立
人群种类分为：病人，潜伏期患者，移出者，群体移出者，死亡者和健康者。

图 五 9人群种类转化示意图
病人在单位时间内的增加量为，潜伏期患者的转化量减去病人治愈数、死亡数和获得群体免疫的人群数，所以
(dI(t))/dt=∑_(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗(t-i)-μi(t)〗-dI(t)-w(t)i(t)
单位时间潜伏期患者数变化量为，健康人转化为潜伏期患者的数量减去转化为病人的数量，故
(dQ(t))/dt=-∑(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗_(t-i) 〗+λ(t)s(t)[I(t)+Q(t)]
单位时间健康人变化量为减少的健康人数量
(dS(t))/dt=-λ(t)s(t)[I(t)+Q(t)]
有效感染函数可写为
(dλ(t))/dt=k^’ λ(t)s(t)
单位时间内移出者的变化量为治愈的病人的变化量
(dR(t))/dt=μ^’ I(t)
单位时间死亡者的变化量为死亡率乘病人数量
(dD(t))/dt=d^’ I(t)
单位时间群体移出者的变化量，与免疫函数乘病人比例函数成比
(dW(t))/dt=k^’’ W(t)I(t)
有效传播指数和非免疫人群比例的乘积为1时，恰好是临界接种水平 ，即是病毒的传播被遏止了。故可以得到公式：
λ(t)(1-Vc)=1
而当λ(t)(1-Vc)>1时，传染病就会继续传播，而当λ(t)(1-Vc)<1时，传染病随时间而慢慢停息。
以上预测的前提是感染后的幸存者获得完美的免疫力，事实往往是不尽如人意的。因此我们还要加上一个参数L(疫苗对抗传播的有效性),来表达在感染过程中免疫的效果。最后得到公式为
λ(t)(1-Vc*L)=1
Vc=(1-1/λ(t))/L
故当L<1时，即感染后的免疫效果并不完美时，需要更大的Vc, 即更大比例的病人和移出者，才能阻遏传染病。
5.3.4模型的求解
取定初值为[0.0001 0.0003 0.9996 2.68 0 0.0503 0.0001]，分别对应病人，潜伏期患者，健康人，有效传染指数，移出者，死亡率和移出者，采用Matlab编程计算。

图 五 10病人、健康人、移出者、群体免疫变化趋势图
如图所示，自3月24日之后的29.18天，病人比例达到0.7143，此时由λ(t)*(1-Vc)>=1知，研究对象获得了群体免疫。最后，群体移出者占总人数的0.6761，移出者占0.0878。由5.03%的死亡率知，这次疫情将死去228.97万人。
5.3.5模型的改进
模型三中未对加强措施之后进行分析，在某种程度上产生了一部分失真，在其基础上建立第二阶段的模型改变其中的参数来预测政府采取措施之后的情况更佳。
5.4问题四
经济发展与人类资源，资金和技术等等因素息息相关。病情影响经济发展，尤其是需要人力资源的行业，比如说包装业。本模型在模型一的基础上加以改进，结合经济增长模型和道格拉斯函数，对包装行业经济发展进行预测。其中和模型一一样，分为防控前和防控后，详细如下：
5.4.1模型的建立
劳动力与健康人和移出者占总人数的比例有关，故引用模型一的公式来解决问题，在第一阶段，没有进行很严格的防控，故此时的五种人比例变化情况分别为
(dI(t))/dt=∑_(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗(t-i)-ui(t)〗-dI(t)
(dQ(t))/dt=-∑(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗(t-i) 〗+λ(t)s(t)[I(t)+Q(t)]
(dS(t))/dt=-λ(t)s(t)[I(t)+Q(t)]
(dλ(t))/dt=kλ(t)s(t)
(dD(t))/dt=dI(t)
(dR(t))/dt=μI(t)
产值与资金、劳动力和技术有关，所以有
Q(t)=f_0 〖L(t)〗^α 〖K(t)〗^β
两边同时取对数有,其中α和β为对应函数的待测算参数
Ln Q(t)=Lnf_0+αLn L(t)+βLn K(t)
而时间内劳动力的变化量为，移出者减去健康人转化为潜伏期患者的数量，h为可参加劳动者中为劳动者的比例
(dL(t))/dt=μI(t)-λ(t)S(t)(I(t)+Q(t))
单位时间间隔内资金的变化量与产值成比例，g为比例系数
(dK(t))/dt=gP(t)
在第二阶段，由于进行了必要的防控，其使得一些量发生了变化。具体情况如下：
(dI(t))/dt=∑(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗(t-i)-μ_1 i(t)〗-dI(t)
由于此时防控力度的加大，使得感染率大大降低，此时潜伏期人数所占比例变化为：
(dQ(t))/dt=-∑(j=2)^{14▒〖∑_(i=2)}j▒α_i 〖Q(t)〗_(t-i) 〗+cλ(t)s(t)[I(t)+Q(t)]
大力干预，使得健康人下降的比例大量减少：
(dS(t))/dt=-cλ(t)s(t)[I(t)+Q(t)]
病人的治愈率大大提高
(dR(t))/dt=μ_1 I(t)
其他参数基本不变:
(dλ(t))/dt=kλ(t)s(t)
dD(t)/dt=dI(t)

5.4.2模型的求解
通过Matlab对第一阶段的产值变化情况进行求解，设其产量初值为1584.15万元，则解题情况为下图：

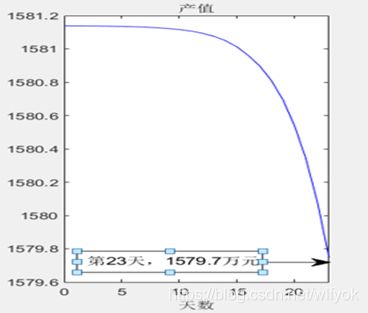
图 五 11产值趋势图
由图分析得到，产值一直保持稳定，在大约10天左右开始下降，到第23天左右下降到1579.7万元，这时开始由于开始干预，导致其出现了一些变化。进入第二阶段，其求解情况如下：

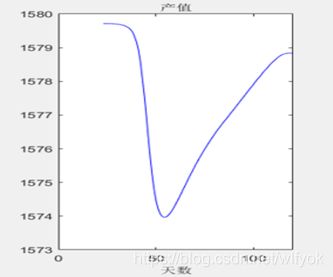
图 五 12产值趋势图
由图我们可以知道，在进行疫情防控之后的一段时间后，企业的产值开始出现上升。
5.4.3模型的改进
对于模型四的改进，模型四中仅考虑了对劳动力对其的影响，若在此基础上综合考虑多种因素利用层次分析法进行权重的判断从而建立更有效地模型来预测未来变化更加。

模型的分析

6.1模型的误差分析

1. 在模型一中。将治愈率的值设为一简单的函数。但是在实际情况平均每个人每天所接触的人数和他每接触一个人患病概率的乘积，它也会产生一定的误差。下面对模型一进行检验适当，之后模型也用类似方法。
   在已知u=5.2求σ^{2的置信区间，枢轴量((n-1)s}2)/σ^2 ~X^2 (n-1)，且满足条件P(X_(α/2)≤((n-1) s^2)/σ2 ≤X_(1-α/2) )=1-α
   考虑括号内的不等式解得σ^2的置信区间为[((n-1) s^{2)/(X_(1-α/2)}2 (n-1) ),((n-1) s^2)/(X_(α/2)2 (n-1) )]，取定1-α=0.95，查表得X_0.025 (100)=129.56〖,X〗_0.975 (100)=74.22带入数据可得置信度为0.95的置信区间为[2.5551.4603]，可见估计效果良好符合实际。

2.模型二中将其假设为自由传播，但在实际情况中居民会采取一定的措施，还有就是在达到一定程度后会进行适当的防控，未考虑到。
3.模型四中对产值的影响仅考虑了劳动力的影响，并未考虑对其的一些措施产生的影响。

参考文献

[1] https://zhuanlan.zhihu.com/p/113393938
[2] https://blog.csdn.net/Zengmeng1998/article/details/104231869
[3] 王建宁. 河北省人才资本对经济增长的贡献研究[D]. 首都经济贸易大学.
[4] 数学模型（第五版）姜启源、谢金星、叶俊 高等教育出版社 2018-05-23
[5] https://www.zhihu.com/question/367643582/answer/984277887

附录

%滞后变量权数的求解
suiji=rand(1,100)*12;
mean(suiji)
xigama=std(suiji)
zhengtai=normrnd(5.2,3.3439,1,2000);
mean(zhengtai)
i=1:100;
j=1:2000;
subplot(1,2,1),plot(i,b,'b-')
xlabel('人数序号'),ylabel('天数');
subplot(1,2,2),plot(j,R,'g')
xlabel('人数序号'),ylabel('天数')               %100人中潜伏期的爆发时间分布与正态模拟
syms x;
zhengtai_hanshu=1/(xigama*sqrt(2*pi))*exp(-(x-5.2)^2/(2*xigama^2));
for i=1:13
    aerfa(i)=int(zhengtai_hanshu,i+1+0.5,i+1-0.5);
end
aerfa=vpa(aerfa/sum(aerfa))      %权系数的归一化与输出

 %置信区间上下限的计算
kafang(1)=74.22;
kafang(2)=129.56;
n=100;
for i=1:2
    zh(i)=(n-1)*xigama/(kafang(i));
end

%问题一的求解
[i,q,s,m,d]=dsolve('Di=q-0.1*i-0.04*i','Dq=-q+m*s*(i+q)','Ds=-m*s*(i+q)','Dm=m*s','Dd=0.04*i','t');
%无法找到解析解，从而转向求数值解
function dy=crb(t,y)
% 此函数文件用来解 2020.3的华为杯传染病模型问题1.1
dy=zeros(5,1);
dy(1)=y(2)-0.1*y(1)-0.04*y(5);
dy(2)=-y(2)+y(4)*y(3)*(y(1)+y(2));
dy(3)=-y(4)*y(3)*(y(1)+y(2));
dy(4)=0.1134*y(4)*y(3);
dy(5)=0.04*y(1);
%
[T,Y]=ode45(@crb11,[0,50],[0.0000575 0 0.9999525 15 0.0217])
t=0:length(T)-1;
subplot(1,3,1),plot(t,Y(:,1),'g'),xlabel('天数'),ylabel('病人比例'),xlim([0,200]),text(23,0.0007,'第23天，0.0007')
subplot(1,3,2),plot(t,Y(:,4),'b'),xlabel('天数'),ylabel('有效传播指数'),xlim([0,200])
subplot(1,3,3),plot(t,Y(:,5),'r'),xlabel('天数'),ylabel('死亡率'),xlim([0,200])
%
function dy=crb2(t,y)
% 此函数文件用来解 2020.3的华为杯传染病模型问题1.2
dy=zeros(5,1);
dy(1)=y(2)-0.04*y(5);
dy(2)=-y(2)+y(4)*y(3)*y(2);
dy(3)=-y(4)*y(3)*y(2);
dy(4)=0.1134*0.1*y(4)*y(3);
dy(5)=0.04*y(1);
%
[T,Y]=ode45(@crb12,[0,50],[0.0007 0.008 0.9843 0 0.0217])
t=27:length(T)-1+27
plot(t,Y(:,1),'p')
xlabel('天数'),ylabel('病人比例')
text(23,0.0007,'第23天，0.0007'),text(47,0.0058,'第47天，0.0058')
xlim([0,72])

% 第二问
function dy=crb2(t,y)
% 此函数用来求解问题2.1
dy=zeros(6,1);
dy(1)=y(2)-0.1*y(1)-0.04*y(5)+5.4054e-08;
dy(2)=-y(2)+y(4)*y(3)*(y(1)+y(2));
dy(3)=-y(4)*y(3)*(y(1)+y(2));
dy(4)=0.1134*y(4)*y(3);
dy(5)=0.04*y(1);
dy(6)=0.1*y(1);
[T,Y]=ode45(@crb21,[0,50],[0 0 1 12 0 0])
%
t=0:length(T)-1;
plot(t,Y(:,1),'g'),ylabel('病人比例'),xlabel('天数'),xlim([0,10])
% subplot(2,4,3),plot(t,Y(:,2),'b'),title('潜伏期患者'),xlabel('天数'),xlim([0,20])
% subplot(2,4,4),plot(t,Y(:,3),'b'),title('健康人'),xlabel('天数'),xlim([0,20])
% subplot(2,4,5),plot(t,Y(:,4),'b'),title('有效感染指数'),xlabel('天数'),xlim([0,20])
% subplot(2,4,6),plot(t,Y(:,5),'b'),title('死亡率'),xlabel('天数'),xlim([0,20])
% subplot(2,4,7),plot(t,Y(:,6),'b'),title('移出者'),xlabel('天数'),xlim([0,20])
%
function dy=crb2(t,y)
% 此函数文件用来解 2020.3的华为杯传染病模型问题2.2
dy=zeros(6,1);
dy(1)=y(2)-0.04*y(1)-0.2*y(1);
dy(2)=-y(2)+y(4)*y(3)*y(2);
dy(3)=-y(4)*y(3)*y(2);
dy(4)=0.1134*0.01*y(4)*y(3);
dy(5)=0.04*y(1);
dy(6)=0.1*y(1);
%
[T,Y]=ode45(@crb22,[0,50],[4.46e-6 5.814e-5 1 0.5 1.422e-8 3.555e-8])
t=9:length(T)+9-1;
plot(t,Y(:,1),'r'),ylabel('病人比例'),xlabel('天数'),xlim([0,50])
% subplot(2,4,3),plot(t,Y(:,2),'b'),title('潜伏期患者'),xlabel('天数'),xlim([0,20])
% subplot(2,4,4),plot(t,Y(:,3),'b'),title('健康人'),xlabel('天数'),xlim([0,20])
% subplot(2,4,5),plot(t,Y(:,4),'b'),title('有效感染指数'),xlabel('天数'),xlim([0,20])
% subplot(2,4,6),plot(t,Y(:,5),'b'),title('死亡率'),xlabel('天数'),xlim([0,20])
% subplot(2,4,7),plot(t,Y(:,6),'b'),title('移出者'),xlabel('天数'),xlim([0,20])

%第三问
%当前英国病人与死亡人数数据图
ttt=1:53;
it=[2 2 2 2 2 2 2 3 3 3 4 8 8 9 9 9 9 9 9 9 9 9 9 9 9 13 13 13 16 20 23 36 39 51 89 118 167 210 277 323 376 460 594 802 1144 1395 1547 2630 3277 3983 5018 5687 6654];
dt=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 2 3 6 6 8 10 21 35 55 55 103 144 177 233 287 335];
subplot(1,2,1),plot(ttt,it)
xlabel('天数'),ylabel('人数')
subplot(1,2,2),plot(ttt,dt)
xlabel('天数'),ylabel('人数')
%
% 在Matlab中模拟病毒的传播模型
% 数值的建立
M=100;              % 尺寸大小
beta=0.05;          % 感染率
gama=0.01;          % 免疫能力
% 建立网格
y = zeros(M, M);    % 网格x元素的意思是: 0是健康人，1使感染者，2免疫者
% 设置初始网格x，在网格的中心有一圈感染者，半径为10个细胞
for i=1:M
    for j=1:M
        dxx = i-M/2;
        dyy = j-M/2;
        d = sqrt(dxx*dxx+dyy*dyy);
        if ( d<10 )
            y(i,j)=1;
        end
    end
end
% 定义社区，也就是最近的8个邻居
lingju = [-1 -1; 0 -1; 1 -1; 1 0; 1 1; 0 1; -1 1; -1 0];
% 创造一个新的窗口
figure
hold on
% 主循环，迭代时间变量t
for t=1:100000
    % 遍历网格 x 中的所有单元格，对于索引 i 1从n 和 j 从1到 n
    for i=1:M
        for j=1:M
            % 在邻居之间来回走动，传播疾病
            for k=1:8
                i2 = i+lingju(k, 1);
                j2 = j+lingju(k, 2);
                % 检查细胞是否在网格边界内
                if ( i2>=1 && j2>=1 && i2<=M && j2<=M )
                    %如果细胞处于易感状态和邻近细胞
                    % 被感染的传播感染的概率是beta
                    if ( y(i,j)==0 && y(i2, j2)==1 )
                        if ( rand<beta )
                            y(i,j) = 1;
                        end
                    end
                end
            end
            % 如果被感染的人能够以伽马的概率从疾病中康复
            if ( y(i,j)==1 && rand<gama )
                y(i,j) = 2;
            end
        end
    end
    % 动态模拟
    clf
    imagesc(y, [0 2])                   % 网格展示
    pause(0.01)                         % 暂停0.01s
    colormap([1 0 1; 1 1 0; 1 1 1]);    % 定义0、1、2分别对应的颜色
    % 如果没有更多的感染者，就停止模拟
    if ( sum(y==1)==0 )
        break;
    end
end
%
% 问题3模型的求解
function dy=crb3(t,y)
% 此函数用来求解模型的第三问
dy=zeros(6,1);
dy(1)=y(2)-0.0203*y(1)-0.0503*y(1)-y(6)*y(1);
dy(2)=-y(2)+y(4)*y(3)*(y(1)+y(2));
dy(3)=-y(4)*y(3)*(y(1)+y(2));
dy(4)=2.68*y(4)*y(3);
dy(5)=0.0203*y(1)
dy(6)=0.0503*y(1);
dy(7)=y(6)*y(1);
%
[T,Y]=ode45(@crb3,[0,50],[0.0001 0.0003 0.9996 2.68 0 0.0503 0.0001])
t=0:length(T)-1;
subplot(2,2,1),plot(t,Y(:,1),'r'),title('病人'),xlabel('天数'),xlim([0,250]),text(122,0.7143,'第122天，0.7143')
subplot(2,2,2),plot(t,Y(:,3),'b'),title('健康人'),xlabel('天数'),xlim([0,250])
subplot(2,2,3),plot(t,Y(:,5),'r'),title('移出者'),xlabel('天数'),xlim([0,250])
subplot(2,2,4),plot(t,Y(:,7),'k'),title('群体免疫'),xlabel('天数'),xlim([0,250]),text(29.18,0.7143,'第240天，0.6929')

% 问题四的求解
% 尚未封城阶段
function dy=crb41(t,y)
% 此函数用来解决问题4.1
dy=zeros(7,1)
dy(1)=0.1*y(2)-y(5)*y(4)*(y(2)+y(3));
dy(2)=y(3)-0.1*y(2)-0.0217*y(7);
dy(3)=-y(3)+y(5)*y(4)*(y(2)+y(3));
dy(4)=-y(5)*y(4)*(y(2)+y(3));
dy(5)=0.1134*y(5)*y(4);
dy(6)=0.1*y(2);
dy(7)=0.0217*y(2);

function dy=crb42(t,y)
% 此函数用来解决问题4.2
dy=zeros(7,1)
dy(1)=0.1*y(2)-y(5)*y(4)*y(3);
dy(2)=y(3)-0.1*y(2)-0.0217*y(7);
dy(3)=-y(3)+y(5)*y(4)*y(3);
dy(4)=-y(5)*y(4)*y(3);
dy(5)=0.1134*y(5)*y(4);
dy(6)=0.1*y(2);
dy(7)=0.0217*y(2);

%采取防控前
[T,Y]=ode45(@crb41,[0,50],[100 0.0000575 0 0.9999525 12 0 0.0217])
K=1000;f0=5;
F=f0*Y(:,1).^0.5*K^0.5;
t=0:length(T)-1;
subplot(1,2,1),plot(t,F,'b'),title('产值'),xlabel('天数'),xlim([0,23])
% 采取防控措施后
[T,Y]=ode45(@crb42,[0,50],[99.82 0.0007 0.0009 0.9984 1 0.0001 0.0217])
K=1000;f0=5;
F=f0*Y(:,1).^0.5*K^0.5;
t=23:length(T)+23-1;
subplot(1,2,2),plot(t,F,'b'),title('产值'),xlabel('天数'),xlim([0,120])