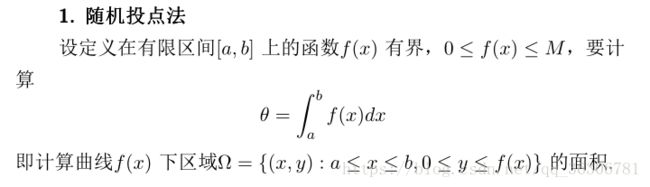R学习之蒙特卡罗积分 --(R语言编程)-----数模
-
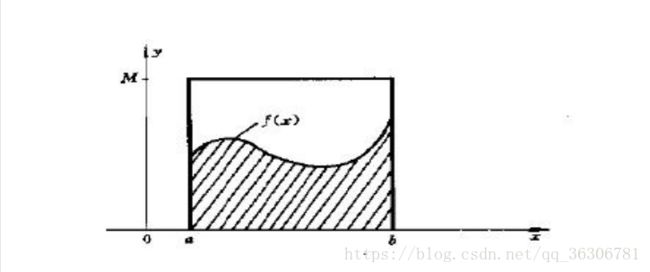
- 蒙特卡罗方法介绍
- 问题1
- 其中函数说明
- 结果
- 问题2
- 结果
- 问题3
- 结果
- 问题4
- 结果
- 问题5
- 结果
- 问题6
- 结果
- DONE!!!
蒙特卡罗方法介绍
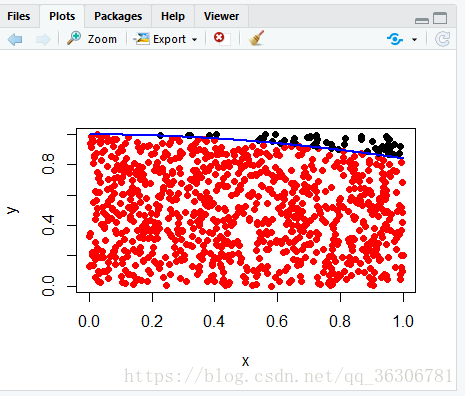
问题1
∫10sin(x)xdx ∫ 0 1 s i n ( x ) x d x
R语言编程:
#0到1 sin(x)/x积分(投点法)
n=1000
x=runif(n);y=runif(n)
g<-function(x) sin(x)/x
length(x[y<=g(x)])/n #sum(y<=g(x))/n
plot(x,y,pch=16,col=c((y<=g(x))+1))
lines(sort(x),g(sort(x)),col="blue",lwd=2)或直接套用函数(都可以用)
integrate(g,0,1)其中函数说明
- x[y<=g(x)]表示取y<=g(x)的x位置处的x
> x=c(1,3,6,9,2)
> m=c(TRUE,FALSE,TRUE,FALSE,TRUE)
> x[m]
[1] 1 6 2- plot()
作图工具
用法:plot(x, y, ……)
参数:
pch:指定绘制点所使用的符号,取值范围[0, 24],其中4是“差号”,20是“点”
pch=16也表示点
col:默认绘图颜色。某些函数(如lines、pie)可以接受一个含有颜色值的向量,并自动循环使用。
例如:col=c(“red”, “blue”)需要绘制三条线,那么三条颜色分别为red、blue、red
col=1表示黑点,col=2表示红点
> m
[1] TRUE FALSE TRUE FALSE TRUE
> c(m+1)
[1] 2 1 2 1 2其他参数见网址
- sort()
对向量x进行从小到大排序,返回值排序后的数值向量
> x<-c(97,93,85,74,32,100,99,67)
> sort(x)
[1] 32 67 74 85 93 97 99 100其他关于排序的见网址
- line()
函数lines()其作用是在已有图上加线,命令为lines(x,y),其功能相当于plot(x,y,type=”1”),不用上sort则会是回折的的线,所以用上sort。
col指定颜色,lwd指定宽度
更多关于画图的见网址
结果
> n=1000
> x=runif(n);y=runif(n)
> g<-function(x) sin(x)/x
> length(x[y<=g(x)])/n #sum(y<=g(x))/n
[1] 0.945
> plot(x,y,pch=16,col=c((y<=g(x))+1))
> lines(sort(x),g(sort(x)),col="blue",lwd=2)问题2
∫10(cos50x+sin20x)2dx ∫ 0 1 ( c o s 50 x + s i n 20 x ) 2 d x
R语言编程:
#0到1 (cos50x+sin20x)^2积分(投点法)
n=10000
x=runif(n);y=runif(n,0,4)
g<-function(x) {(cos(50*x)+sin(20*x))^2}
p<-length(x[y<=g(x)])/n;i<-4*p;i结果
> n=10000
> x=runif(n);y=runif(n,0,4)
> g<-function(x) {(cos(50*x)+sin(20*x))^2}
> p<-length(x[y<=g(x)])/n;i<-4*p;i
[1] 0.9544问题3
∫2−2ex+x2dx ∫ − 2 2 e x + x 2 d x
R语言编程:
#-2到2 e^(x+x^2)积分(平均值法)
f1=function(n,a,b,f){
x=runif(n)
sum((b-a)*f(a+(b-a)*x))/length(z)
}
n=100000;a=-2;b=2
f=function(x) {\exp(x+x^2)}
f1(n.a,b,f)
#或(内置函数)
integrate(f,a,b)结果
> #-2到2 e^(x+x^2)积分(平均值法)
> f1=function(n,a,b,f){
+ x=runif(n)
+ sum((b-a)*f(a+(b-a)*x))/length(x)
+ }
> n=100000;a=-2;b=2
> f=function(x) {exp(x+x^2)}
> f1(n,a,b,f)
[1] 93.95082
> #或(内置函数)
> integrate(f,a,b)
93.16275 with absolute error < 0.00062问题4
∫10∫10e(x+y)2dxdy ∫ 0 1 ∫ 0 1 e ( x + y ) 2 d x d y
R语言编程
#0到1 0到1 e^(x+y)^2(平均值法)
x=runif(100000,0,1)
y=runif(100000,0,1)
f=function(x,y) exp((x+y)^2)
sum(1*1*f(x,y))/length(x)结果
> #0到1 0到1 e^(x+y)^2(平均值法)
> x=runif(100000,0,1)
> y=runif(100000,0,1)
> f=function(x,y) exp((x+y)^2)
> sum(1*1*f(x,y))/length(x)
[1] 4.88204问题5
∫101−x2−−−−−√ ∫ 0 1 1 − x 2
R语言编程:
#0到1 sqrt(1-x^2)
#(投点法)
n=100000
x=runif(n,0,1);y=runif(n,0,1)
g=function(x) sqrt(1-x^2)
1*1*length(x[y<=g(x)])/length(x)
#(平均值法)
n=10000
x=runif(n,0,1)
1*sum(sqrt(1-x^2))/length(x)结果
> #0到1 sqrt(1-x^2)
> #(投点法)
> n=100000
> x=runif(n,0,1);y=runif(n,0,1)
> g=function(x) sqrt(1-x^2)
> 1*1*length(x[y<=g(x)])/length(x)
[1] 0.7854
>
> #(平均值法)
> n=10000
> x=runif(n,0,1)
> 1*sum(sqrt(1-x^2))/length(x)
[1] 0.7814675问题6
(1)
∫10eexdx ∫ 0 1 e e x d x
(2)
∫∞0x(1+x2)−2dx ∫ 0 ∞ x ( 1 + x 2 ) − 2 d x
(3)
∫10xsinxdx ∫ 0 1 x s i n x d x
(4)
∫10sin(ex)dx ∫ 0 1 s i n ( e x ) d x
R语言编程:
#(1)
#0到1 e^(e^x)
f=function(x) exp(exp(x))
integrate(f,0,1)
#(2)
#0到∞ x(1+x^2)^-2
f=function(x) x*(1+x^2)^(-2)
integrate(f,0,Inf)
#(3)
#0到1 x*sinx
f=function(x) x*sin(x)
integrate(f,0,1)
#(4)
#0到1 sin(e^x)
f=function(x) sin(exp(x))
integrate(f,0,1)结果
> #(1)
> #0到1 e^(e^x)
> f=function(x) exp(exp(x))
> integrate(f,0,1)
6.316564 with absolute error < 7e-14
> #(2)
> #0到∞ x(1+x^2)^-2
> f=function(x) x*(1+x^2)^(-2)
> integrate(f,0,Inf)
0.5 with absolute error < 3.3e-09
> #(3)
> #0到1 x*sinx
> f=function(x) x*sin(x)
> integrate(f,0,1)
0.3011687 with absolute error < 3.3e-15
> #(4)
> #0到1 sin(e^x)
> f=function(x) sin(exp(x))
> integrate(f,0,1)
0.8749572 with absolute error < 9.7e-15