XCTF-*CTF2022-Alice系列挑战write up

Alice’s warm up

描述

Welcome to the XCTF-*CTF2022, I'm Alice and interested in AI security.
I prepared a easy warm-up for you before you enjoy those pure AI security challenges.
Like humans, AI also needs to warm up before running. Can you find something strange in these initialized parameters?

题面大部分是废话，不过还是有两点有用的信息的：第一点是需要选手关注模型的初始参数(initialized parameters)，第二点是提示这题不是纯粹的AI问题(pure AI security challenges)。

Challenge 1

我在这题中设置的第一个挑战是如何正确载入模型。这个子任务的出发点是希望传达一个观念——AI模型文件和当前的AI模型不同，它是有着完整且清晰结构的文件，而后者更多时候是一个黑漆漆的黑盒。

从比赛网站下载的文件为xxxx.zip，解压后会发现里面有一个archive文件夹，文件夹里面有一个hint.py和若干AI模型文件。这里很多师傅试图直接使用torch.load()导入data.pkl时会发现报错，实际如果熟悉pytorch模型保存的文件结构或者自己尝试保存一个模型，就会发现其实模型本身就是zip格式的，而且结构和得到的zip一样(除了多了个hint.py)。所以最方便的解法就是直接torch.load载入zip。

savepath='./0bdb74e42cdf4a42923ccf40d2a66313.zip'
net=torch.load(savepath)

载入模型之后还需要恢复模型。首先保存信息会提示不存在AliceNet1，其实只需要补上一个空的类就行了。

class AliceNet1(nn.Module):
    pass

当然如果你想知道内部的结构，直接打印就可以知道了。

savepath='./0bdb74e42cdf4a42923ccf40d2a66313.zip'
net=torch.load(savepath)
print(net)
############################################################################################################
AliceNet1(
  (fc): Sequential(
    (0): Linear(in_features=47, out_features=47, bias=True)
    (1): Linear(in_features=47, out_features=10, bias=True)
    (2): Linear(in_features=10, out_features=1, bias=True)
  )
)
############################################################################################################

Challenge 2

开始挑战之前首先让我们回顾一下到目前为止，还有多少提示没有用上。“关注模型的初始参数”和hint.py这些提示没有用上，也没有用上提示“这题不是纯粹的AI问题”。

首先让我们查看一下net中的参数是个什么样的情况。net的结构是一个47X10X1的全连接网络，除了第0层是方阵而其他都是一般的矩阵。通过使用pytorch的state_dict()函数，我们可以观察每层矩阵的参数情况

for name in net.state_dict():
    print(name)
############################################################################################################
fc.0.weight
fc.0.bias
fc.1.weight
fc.1.bias
fc.2.weight
fc.2.bias
############################################################################################################

for name in net.state_dict():
    print(net.state_dict()[name])
############################################################################################################
fc.0.weight
tensor([[0., 0., 1.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        ...,
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]])
fc.0.bias
tensor([-0.0481,  0.0083,  0.0302,  0.0301, -0.0125,  0.1012,  0.0500,  0.0477,
         0.0310,  0.0276, -0.0967,  0.0889, -0.0678, -0.1428,  0.1141, -0.1254,
         0.1439, -0.0778,  0.0316, -0.0729,  0.0046, -0.1126, -0.0916,  0.1256,
         0.0641, -0.0317,  0.0422, -0.1378, -0.0489,  0.0612,  0.0500,  0.0190,
        -0.0649, -0.1008, -0.1050, -0.0399,  0.0906,  0.0275, -0.0825, -0.1431,
         0.1126, -0.0183,  0.1168, -0.0400, -0.0637,  0.0806, -0.0296])
fc.1.weight
tensor([[-0.0512,  0.1195, -0.0837, -0.0519, -0.0278,  0.0530,  0.1385, -0.0872,
         -0.1022, -0.0910, -0.0098,  0.0995,  0.0531, -0.0997, -0.0123, -0.0347,
         -0.0872,  0.0987, -0.0472,  0.0851, -0.1073, -0.0153, -0.0942,  0.0949,
          0.0522,  0.0521,  0.1063,  0.1335,  0.0305,  0.1082,  0.0114, -0.1429,
         -0.1264,  0.1127, -0.1318,  0.0350,  0.1166,  0.1224,  0.0600, -0.0837,
         -0.0425, -0.0854,  0.0214, -0.1391, -0.0359, -0.0529, -0.0379],
         ...
        [-0.0641, -0.1137, -0.0556,  0.1383, -0.0967,  0.0524, -0.0661,  0.0510,
         -0.1030, -0.0732,  0.1109,  0.1101, -0.1164, -0.0505, -0.0610, -0.0219,
         -0.1451, -0.0486, -0.0898, -0.1229,  0.1050, -0.0934, -0.0408,  0.0432,
          0.0159,  0.0220,  0.0875, -0.0512, -0.0437,  0.0833,  0.0277,  0.0892,
         -0.1136, -0.1330, -0.0778,  0.0363,  0.0043,  0.1038, -0.1079, -0.0030,
         -0.0358, -0.1302,  0.0822,  0.0155,  0.0218,  0.0417,  0.1241]])
fc.1.bias
tensor([ 0.0427,  0.1376, -0.0805,  0.1418,  0.1263,  0.0791, -0.0008,  0.0997,
         0.0499, -0.0104])
fc.2.weight
tensor([[-0.2986, -0.2412,  0.2308, -0.0410,  0.1583, -0.0777, -0.2521,  0.0848,
         -0.0169, -0.0387]])
fc.2.bias
tensor([-0.1993])
############################################################################################################

可以发现除了第一个方阵为0-1矩阵，其他参数都在[-1,1]之间。第一个方阵是比较特别的。

现在再看看hint.py，flagset告知了flag的内容选择范围以及flag格式，同时也告知了flag的长度。可以发现，flagset中的字母数量正好为47。

import string
assert len(flag)==16
assert flagset=string.printable[0:36]+"*CTF{ALIZE}"

首先第一步是找出flagset与0-1矩阵之间的关系，这里可以大胆猜测flagset的字母和0-1矩阵的行列是一一对应的，也就是矩阵是一个邻接矩阵。这可以通过分析字母之间的相关性得到——*CTF{是连在一起的且没有其他分支，}只和字母r相连。不过进一步的分析会发现，整个邻接矩阵代表的是一个带环的有向图。对于破解flag，flag的长度是需要知道的。我们可以使用dfs来完成这个工作，最大深度设置为16，初始位置为"*"。完整exp的如下

import torch
from torch import nn
import string
class AliceNet1(nn.Module):
    pass
def char2num(ch):
    tmpset = string.printable[0:36]+'*CTF{ALIZE}'
    tmplen=len(tmpset)
    for i in range(tmplen):
        if(ch==tmpset[i]):
            return i
def dfs(ch,depth,ans):
    ans+=ch
    if(len(ans)==flaglen and ans[-1]=='}'):
        print('flag is:',ans)
    elif(len(ans)==flaglen):
        return
    else:
        tmpi=char2num(ch)
        for i in range(setlen):
            if(flagset[i]==ch):
                continue
            tmpj=char2num(flagset[i])
            if(mymat[tmpi][tmpj]==1.0 and used[tmpj]==False):
                used[tmpj]=True
                dfs(flagset[i],depth+1,ans)
                used[tmpj]=False
savepath='./0bdb74e42cdf4a42923ccf40d2a66313.zip'
net=torch.load(savepath)
print(net)
mymat=net.state_dict()['fc.0.weight'].tolist()
flagset=string.printable[0:36]+'*CTF{ALIZE}'
setlen=len(flagset)
flaglen=10+6
used=[False]*setlen
flag=''
used[char2num('*')]=True
dfs('*',0,flag)
############################################################################################################
flag is: *CTF{qx1jukznmr}
############################################################################################################

可以看出第二部分的解法其实是和AI无关的，也就是不是纯的AI题目。然后就是这题比较难分析出的点在于0-1矩阵的含义，这一点实际上当初出题的时候有考虑到，也准备了hint dfs。

不过由于实际解题情况，最终就没有放了。给各位师傅带来困扰了，我在这里真诚的道歉QAQ。

Alice’s challenge

这是一题就是一道纯的AI安全的题目了，出这题的目的在于和大家分享一种隐私攻击方法——梯度泄露攻击(毕竟大家做FGSM也做腻了对吧)。题目的来源是NeurlPS 2019的论文《Deep leakage from gradient》中的开源代码。

https://github.com/mit-han-lab/dlg

由于这题的出题目的是分享算法，所以解题只需要通过搜索诸如"从梯度恢复图像"这种短句就可以找到很多恢复算法以及对应的代码。之后稍微理解一下修改对应的代码即可获得答案。一些介绍这种算法以及对应代码的链接如下

https://zhuanlan.zhihu.com/p/476936278
https://github.com/JonasGeiping/breaching
https://www.anquanke.com/post/id/259060#h3-4

简单修改了dlg-master中的代码得到exp

from PIL import Image
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import transforms

class AliceNet2(nn.Module):
    def __init__(self):
        super(AliceNet2, self).__init__()
        self.conv = \
            nn.Sequential(
            nn.Conv2d(3,12,kernel_size=5,padding=2,stride=2),
            nn.Sigmoid(),
            nn.Conv2d(12,12,kernel_size=5,padding=2, stride=2),
            nn.Sigmoid(),
            nn.Conv2d(12,12,kernel_size=5,padding=2,stride=1),
            nn.Sigmoid(),
            nn.Conv2d(12,12,kernel_size=5,padding=2,stride=1),
            nn.Sigmoid(),
        )
        self.fc = \
            nn.Sequential(
            nn.Linear(768, 200)
        )

    def forward(self, x):
        x = self.conv(x)
        x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x

def criterion(pred_y, grand_y):
    # This is the Cross entropy loss function
    tmptensor=torch.mean(
        torch.sum(
            - grand_y * F.log_softmax(pred_y, dim=-1), 1
        ))
    return tmptensor

ts1 = transforms.Compose([transforms.Resize(32),transforms.CenterCrop(32),transforms.ToTensor()])
ts2 = transforms.ToPILImage()

my_device = "cpu"
if torch.cuda.is_available():
    my_device = "cuda"

Net = torch.load('./Net.model').to(my_device)
outpath='./grad/'

torch.manual_seed(0)

for i in range(25):
    original_dy_dx=dy_dx=torch.load(outpath+str(i)+'.tensor')
    dummy_data = torch.randn(1,3,32,32).to(my_device).requires_grad_(True)
    dummy_label = torch.randn(1,200).to(my_device).requires_grad_(True)
    optimizer = torch.optim.LBFGS([dummy_data, dummy_label])
    history = []
    for iters in range(300):
        def closure():
            optimizer.zero_grad()
            pred = Net(dummy_data)
            dummy_onehot_label = F.softmax(dummy_label, dim=-1)
            dummy_loss = criterion(pred,
                                   dummy_onehot_label)
            dummy_dy_dx = torch.autograd.grad(dummy_loss, Net.parameters(), create_graph=True)
            grad_diff = 0
            grad_count = 0
            for gx, gy in zip(dummy_dy_dx, original_dy_dx):
                grad_diff += ((gx - gy) ** 2).sum()
                grad_count += gx.nelement()
            grad_diff.backward()
            return grad_diff

        optimizer.step(closure)
        if iters % 10 == 0:
            current_loss = closure()
            print(iters, "%.4f" % current_loss.item())
        history.append(ts2(dummy_data[0].cpu()))

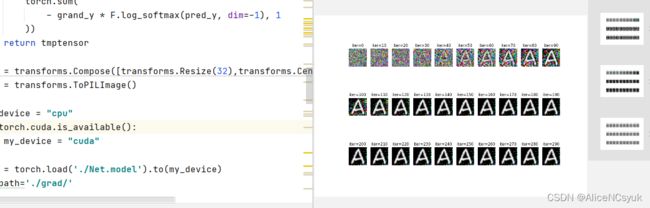
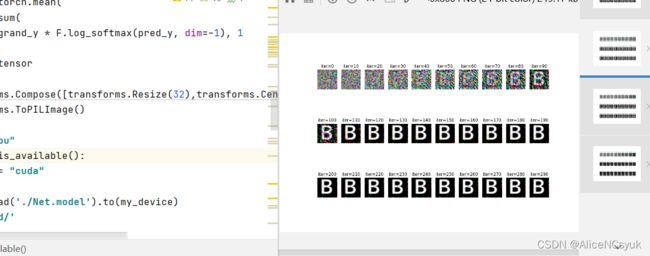
    plt.figure(figsize=(12, 8))
    for i in range(30):
        plt.subplot(3, 10, i + 1)
        plt.imshow(history[i * 10])
        plt.title("iter=%d" % (i * 10))
        plt.axis('off')
    print("Dummy label is %d." % torch.argmax(dummy_label, dim=-1).item())
    plt.show()

效果示例如下


原始flag图片如下

flag: *CTF{PZEXHBEARAK8MQT5NAliceE}