强化学习 7—— 一文读懂 Deep Q-Learning(DQN)算法
上篇文章强化学习——状态价值函数逼近介绍了价值函数逼近(Value Function Approximation,VFA)的理论,本篇文章介绍大名鼎鼎的DQN算法。DQN算法是 DeepMind 团队在2015年提出的算法,对于强化学习训练苦难问题,其开创性的提出了两个解决办法,在atari游戏上都有不俗的表现。论文发表在了 Nature 上,此后的一些DQN相关算法都是在其基础上改进,可以说是打开了深度强化学习的大门,意义重大。
论文地址:Mnih, Volodymyr; et al. (2015). Human-level control through deep reinforcement learning
一、DQN简介
其实DQN就是 Q-Learning 算法 + 神经网络。我们知道,Q-Learning 算法需要维护一张 Q 表格,按照下面公式来更新:
Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ m a x a Q ( S t + 1 , a ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \; max_aQ(S_{t+1}, a) - Q(S_t, A_t)] Q(St,At)←Q(St,At)+α[Rt+1+γmaxaQ(St+1,a)−Q(St,At)]
然后学习的过程就是更新 这张 Q表格,如下图所示:
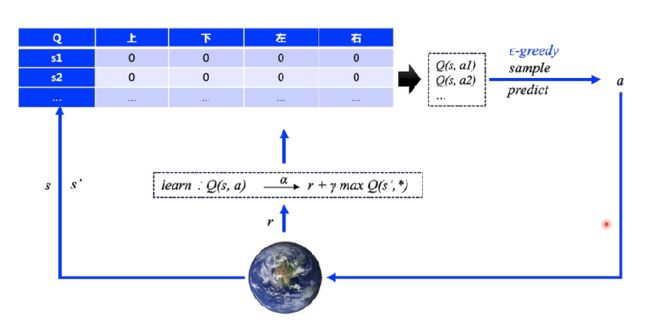
而DQN就是用神经网络来代替这张 Q 表格,其余相同,如下图:
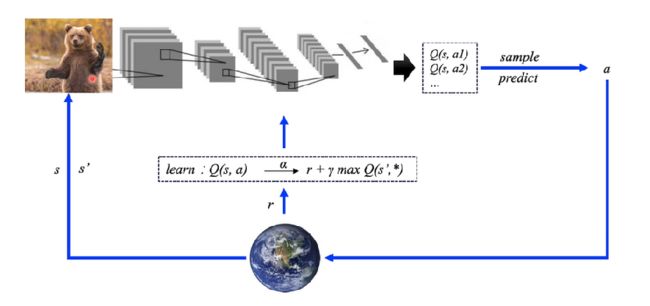
其更新方式为:
Q ( S t , A t , w ) ← Q ( S t , A t , w ) + α [ R t + 1 + γ m a x a q ^ ( s t + 1 , a t , w ) − Q ( S t , A t , w ) ] Q(S_t, A_t, w) \leftarrow Q(S_t, A_t, w) + \alpha[R_{t+1} + \gamma\;max_a\; \hat{q}(s_{t+1}, a_t, w) - Q(S_t, A_t, w)] Q(St,At,w)←Q(St,At,w)+α[Rt+1+γmaxaq^(st+1,at,w)−Q(St,At,w)]
其中 Δ w \Delta w Δw :
Δ w = α ( R t + 1 + γ m a x a q ^ ( s t + 1 , a t , w ) − q ^ ( s t , a t , w ) ) ⋅ ∇ w q ^ ( s t , a t , w ) \Delta w = \alpha ({\color{red}R_{t+1} + \gamma\;max_a\; \hat{q}(s_{t+1}, a_t, w)} - \hat{q}{(s_t, a_t, w)})\cdot \nabla_w\hat{q}{(s_t, a_t, w)} Δw=α(Rt+1+γmaxaq^(st+1,at,w)−q^(st,at,w))⋅∇wq^(st,at,w)
二、Experience replay
DQN 第一个特色是使用 Experience replay ,也就是经验回放,为何要用经验回放?还请看下文慢慢详述
对于网络输入,DQN 算法是把整个游戏的像素作为 神经网络的输入,具体网络结构如下图所示:
第一个问题就是样本相关度的问题,因为在强化学习过程中搜集的数据就是一个时序的玩游戏序列,游戏在像素级别其关联度是非常高的,可能只是在某一处特别小的区域像素有变化,其余像素都没有变化,所以不同时序之间的样本的关联度是非常高的,这样就会使得网络学习比较困难。
DQN的解决办法就是 经验回放(Experience replay)。具体来说就是用一块内存空间 D D D ,用来存储每次探索获得数据 < s t , a t , r t , s t + 1 >
- sample:从 D D D 中取出一个 batch 的数据 ( s , a , r , s ′ ) ∈ D (s, a, r, s') \in D (s,a,r,s′)∈D
- 对于取出的样本数据计算 Target 值: r + γ m a x a ′ Q ^ ( s ′ , a ′ , w ) r + \gamma\; max_{a'}\hat{Q}(s',a',w) r+γmaxa′Q^(s′,a′,w)
- 使用随机梯度下降来更新网络权重 w:
Δ w = α ( r + γ m a x a ′ Q ^ ( s ′ , a ′ , w ) − Q ^ ( s , a , w ) ) ⋅ ∇ w Q ^ ( s , a , w ) \Delta w = \alpha (r + \gamma\;max_{a'}\; \hat{Q}(s', a', w) - \hat{Q}{(s, a, w)})\cdot \nabla_w\hat{Q}{(s, a, w)} Δw=α(r+γmaxa′Q^(s′,a′,w)−Q^(s,a,w))⋅∇wQ^(s,a,w)
利用经验回放,可以充分发挥 off-policy 的优势,behavior policy 用来搜集经验数据,而 target policy 只专注于价值最大化。
三、Fixed Q targets
第二个问题是前文已经说过的,我们使用 q ^ ( s t , a t , w ) \hat{q}(s_t, a_t, w) q^(st,at,w) 来代替 TD Target,也就是说在TD Target 中已经包含我了我们要优化的 参数 w。也就是说在训练的时候 监督数据 target 是不固定的,所以就使得训练比较困难。
想象一下,我们把 我们要估计的 Q ^ \hat{Q} Q^ 叫做 Q estimation,把它看做一只猫。把我们的监督数据 Q Target 看做是一只老鼠,现在可以把训练的过程看做猫捉老鼠的过程(不断减少之间的距离,类比于我们的 Q estimation 网络拟合 Q Target 的过程)。现在问题是猫和老鼠都在移动,这样猫想要捉住老鼠是比较困难的,如下所示:

那么我们让老鼠在一段时间间隔内不动(固定住),而这期间,猫是可以动的,这样就比较容易抓住老鼠了。在 DQN 中也是这样解决的,我们有两套一样的网络,分别是 Q estimation 网络和 Q Target 网络。要做的就是固定住 Q target 网络,那如何固定呢?比如我们可以让 Q estimation 网路训练10次,然后把 Q estimation 网络更新后的参数 w 赋给 Q target 网络。然后我们再让Q estimation 网路训练10次,如此往复下去,试想如果不固定 Q Target 网络,两个网络都在不停地变化,这样 拟合是很困难的,如果我们让 Q Target 网络参数一段时间固定不变,那么拟合过程就会容易很多。下面是 DQN 算法流程图:
如上图所示,首先智能体不断与环境交互,获取交互数据 < s , a , r , s ′ > replay memory ,当经验池中有足够多的数据后,从经验池中 随机取出一个 batch_size 大小的数据,利用当前网络计算 Q的预测值,使用 Q-Target 网络计算出 Q目标值,然后计算两者之间的损失函数,利用梯度下降来更新当前 网络参数,重复若干次后,把当前网络的参数 复制给 Q-Target 网络。
关于DQN的实现代码部分我们下篇介绍
参考资料:
- B站 周老师的 强化学习纲要第四课下

