【力扣精选】用一拳超人的方式打开力扣，刷爆算法题 —— 龙卷篇

写在前面

Hello朋友们，我是秋刀鱼，一只活跃于Java区与算法区的新人博主~
欢迎大家加入高校算法学习社区： https://bbs.csdn.net/forums/Suanfa，社区里大佬云集，大家互相交流学习！

---

近一周刷了很多道题，基本上每天都会做上几道LeetCode的算法题，也是总结了很多知识点。这篇文章呢就是跟大家分享一下好题，我将其按照从难到易分为：虎级（简单题）、鬼级（常规题）、龙级（难题）、神级（过难题），友友们可以按照难度自行刷题哦。如果觉得博主写的还不错的话可以关注支持一下：

主页：秋刀鱼与猫

期待你的支持与关注~

---

本期出场嘉宾：战栗的龙卷（龙卷妹妹一生推！）

题目 397.整数替换

题目难度：虎级

题目描述


前去迎战

来自龙卷的提醒：

本题可以使用搜索算法搭配剪枝来解决，但这样时间复杂度会很高。试着寻找更优的操作策略来降低时间复杂度吧。

解题分析

本题的核心思路是：贪心算法。

对于整数$N$,判断我们可以从二进制的角度进行分析：给定起始值 n，求解将其变为(000…0001)2 的最小步数。

题目中两种操作方式，一种是奇数时 +1 或 -1 的方式，另一种是偶数时 /2 的方式。就按照值的减小速度来看，一定是使用 /2 的方式值下降速度会更快。因此在每一次操作时，尽可能让执行一次操作后的值为一个偶数一定是最优解。

对于奇数操作来说，都能得到一个偶数，是选择 +1 还是 -1 操作呢？因为偶数的二进制末尾为0，因此为了尽可能多地获得偶数，就按照能在末尾提供0的数量来选择操作，越多的末尾0代表着下几次的操作能操作更多的偶数：

• 对于 +1 操作而言：最低位必然为 1，此时如果次低位为 0 的话， +1 相当于将最低位和次低位交换；如果次低位为 1 的话，+1 操作将将「从最低位开始，连续一段的 11」进行消除（置零），并在连续一段的高一位添加一个 1；
• 对于 -1 操作而言：最低位必然为 1，其作用是将最低位的 1 进行消除。

因此，对于 x 为奇数所能执行的两种操作，+1 能够消除连续一段的 1，只要次低位为 1（存在连续段），应当优先使用 +1 操作，但需要注意边界$x=3$时的情况（此时选择 -1 操作）。

代码(Java代码）

class Solution {
    public int integerReplacement(int _n) {
        //防止因为Integer.MAX_VALUE+1溢出
        long n = _n;
        int ans = 0;
        while (n != 1) {
            if (n % 2 == 0) {
                n >>= 1;
            } else {
                if (n != 3 && ((n >> 1) & 1) == 1) n++;
                else n--;
            }
            ans++;
        }
        return ans;
    }
}

题目 116. 填充每一个节点的下一个右侧节点指针

题目难度：虎级

---

题目描述


前去迎战

提示：

• 树中节点的数量在 [0, 212 - 1] 范围内
• -1000 <= node.val <= 1000

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

来自龙卷的提醒：

注意二叉树是完美二叉树，那么为了将每一层的结点 next 指针相连接，最简单的方法只需要遍历每一层结点修改指针，用二叉树的层序遍历就能解决。

但如果还需要考虑只能使用常数级的额外空间（不考虑递归栈空间），那么就需要试着借助 next 指针求解。

解题分析 - 普通版


听完龙卷的一顿分析，大致的思路已经出来了。首先每一层结点 next 指向其右侧节点，只需要使用二叉树的层序遍历方式，每一层每一层遍历二叉树。从左到右顺序遍历每一层，因此先遍历到的结点 next 指向后遍历到的结点，最后一个结点的 next 指针为空。这样一来这道题就算是解决了，代码如下：

class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }
        // 初始化队列同时将第一层节点加入队列中，即根节点
        Queue queue = new LinkedList(); 
        queue.add(root);
        // 外层的 while 循环迭代的是层数
        while (!queue.isEmpty()) {
            // 记录当前队列大小
            int size = queue.size();
            // 遍历这一层的所有节点
            for (int i = 0; i < size; i++) {
                // 从队首取出元素
                Node node = queue.poll();
                // 连接
                if (i < size - 1) {
                    node.next = queue.peek();
                }
                // 拓展下一层节点
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
        }
        // 返回根节点
        return root;
    }
}

解题分析 - 进阶

但是上述的代码并不满足进阶情况，因为空间复杂度为 $O(N)$ 不符合要求。需要进一步考虑优化策略。

既然不能存储使用额外空间存储，为了实现类似于层序遍历的操作，解题方法的核心是使用已经建立的 next 指针。

现在逐步开始分析操作过程，

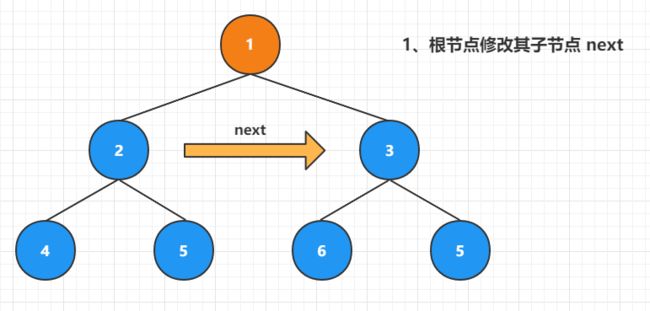
（1）、操作根节点

如上图所示，遍历到的结点为根节点，此时根节点能获取到其子节点的情况。可直接修改其子节点的 next 指针，也就是执行 root.left.next = root.right。而 3 号结点右侧没有新元素，因此其 next 指向空。

（2）、操作 2 号结点：

如上图所示，因为 2 号结点的两个子节点均存在，因此 2 号结点左侧结点的 next 指针一定指向 2 号结点右侧节点，因此可以直接修改。执行 root.left.next = root.right。

而对于 2 号结点的右侧节点，因此 2 号结点的 next 指针在上一层中已经被修改，也就是说 2 号所属的这一层借助 next 指针可以使用层序遍历！而 2 号右侧节点 5 号的 next 值为 2 号 next 指针所指结点 3 号的左侧元素。也就是执行 root.right.next = root.next.left，但执行之前需要判断 2 号结点的 next 元素是否存在。

（3）、继续遍历本层后续结点

现在 2 号元素已经处理完毕，因为 next 指针保证了 2 号这一层能够层序遍历，因此继续遍历 2 号右侧的下一个元素直到遍历元素 next 为空。遍历结束后下面这层的 next 指针也已经确定，同样可以使用层序遍历，继续遍历下一层来确定下下层的next…，最终所有结点的next都能确定完成！

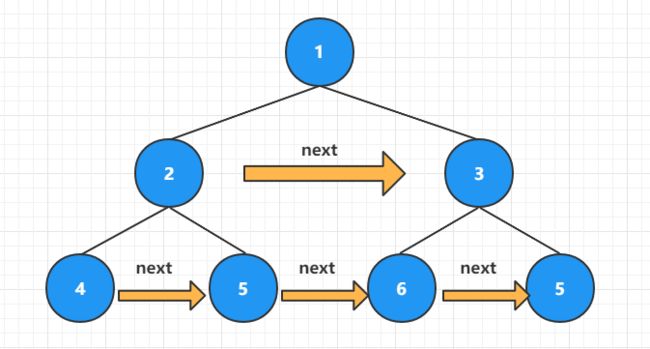
总结一下就是：使用上一层的 next 完成本层的遍历确定下一层的 next ，使用 left 或 right 指针从根向下遍历每一层。

代码

class Solution {
    public:
    Node* connect(Node* root) {
        if (root == nullptr) {
            return root;
        }
        // 从根节点开始
        Node* leftmost = root;
        while (leftmost->left != nullptr) {
            // 遍历这一层节点组织成的链表，为下一层的节点更新 next 指针
            Node* head = leftmost;
            while (head != nullptr) {
                // 连接左结点
                head->left->next = head->right;
                // 连接右节点，需要判断 next是否为空
                if (head->next != nullptr) {
                    head->right->next = head->next->left;
                }
                // 指针向后移动
                head = head->next;
            }
            // 去下一层的最左的节点
            leftmost = leftmost->left;
        }
        return root;
    }
};

题目 117. 填充每个节点的下一个右侧节点指针 II

题目等级：鬼级！

---

题目描述


前去迎战

来自龙卷的提醒：

与上一题不同的地方在于，二叉树从完美二叉树变为了普通二叉树，该变化不影响解题思路，但需要注意遍历时处理的逻辑发生了改变。

因为是完美二叉树，因此能够快速获取下一个结点所在的位置。而在这道题中，各个结点的位置关系都是未知的，怎么处理更好呢？

解题分析

还是上一题的思路，用上一层的结点确定下一层的 next 指向，只不过不是完美二叉树所以处理的逻辑需要考虑。

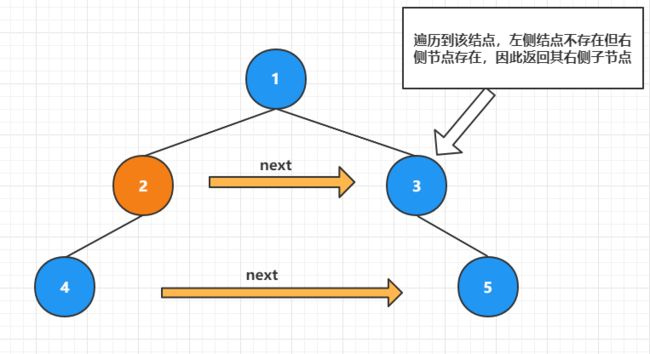
如下图所示，当前遍历的结点是 2 号结点，需要处理 4 号的 next 指向：

因为 2 号结点这一层的 next 指针已经处理完毕，因此找到 4 的 next 指向的方法是，从当前 2 号结点开始向右遍历这一层所有结点，找到拥有子节点的结点返回其左侧子节点，就是 4 号结点的 next 指向。

例如从 2 号结点开始向右查找到 3 号结点，3号结点存在右子节点不存在左子节点，因此返回其右子节点。

此遍历的逻辑封装为函数：getNext(Node *tmp)，返回 tmp 结点这层所有右侧的第一个偏左侧的孩子，如果没有返回为空。

代码

class Solution {
   public:
   Node* getNext(Node* tmp){
       if (tmp == nullptr){
           return nullptr;
       }
       if(tmp->left != nullptr){
           return tmp->left;
       }
       if (tmp->right != nullptr){
           return tmp->right;
       }
       if (tmp->next != nullptr){
           return getNext(tmp->next);
       }
       return nullptr;
   }
   Node* connect(Node* root) {
       if (root == nullptr) {
           return root;
       }
       // 从根节点开始
       Node* leftmost = root;
       while (getNext(leftmost) != nullptr) {
           // 遍历这一层节点组织成的链表，为下一层的节点更新 next 指针
           Node* head = leftmost;
           while (head != nullptr) {
               if (head->left == nullptr && head->right == nullptr){
                   head = head->next;
                   continue;
               }
               if (head->left == nullptr){
                   head->right->next = getNext(head->next);
               }else if(head->right == nullptr){
                   head->left->next = getNext(head->next);
               }else{
                   head->left->next = head->right;
                   head->right->next = getNext(head->next);
               }
               // 指针向后移动
               head = head->next;
           }  
           // 去下一层的最左的节点
           leftmost = getNext(leftmost);
       }
       return root;
   }
};

题目 29. 两数相除

题目难度：鬼级！

题目描述


前去迎战

解题分析

本题禁止使用乘法、除法、取余运算，要求实现 32 为有符号整数的除法运算。

为了实现除法运算，最简单的方式就是将去被除数不断地减除数，直到被除数的值小于除数的值停止，减去除数的次数就是返回的结果值。但是这样代码运行时间会很长，时间上不允许。

倍乘法介绍

我们这里可以考虑使用【倍增乘法】来实现，所谓倍增乘法，简单理解就是每次用被除数减去$[除数的最大\cdot $2^x$]$，这样可以极大地增加处理的速度。

假如给定的值为30，除数为4,使用倍乘法的过程如下：

• 计算$4\times 2^x<=30$的 $x$ 的最大值，计算得 $x=2$ ，执行 $30-4\times 2^2=14$ ，$res+=2^2$。
• 计算$4\times 2^x<=14$的 $x$ 的最大值，计算值 $x=1$ ，执行 $14-4\times 2^1=6$ ，$res+=2^1$。
• 计算$4\times 2^x<=6$的 $x$ 的最大值，计算值 $x=0$ ，执行 $6-4\times 2^0=2$ ，$res+=2^0$。
• 最后 2 小于 4，退出返回 res 即为结果值。

考虑越界情况

因为数值范围固定为$[-2^{31},2^{31}-1]$。有符号数最大值为 $2^{31}-1$，有符号数的最小值为 $-2^{31}$。因为被除数与除数均是有符号数，因此结果值出现越界的情况只有可能是，除数为 INT_MIN 、被除数为-1，此时结果为 $2^{31}$ 越界。因此程序第一步优先判断结果是否越界，即：

if (a == INT_MIN && b == -1) 
    return INT_MAX;

题目中限制环境只能使用 int 型变量，因此在使用被乘法计算时，也有可能出现越界这点也需要单独判断。

在32进制负数的个数比正数数量多1，因此将正数转换为负数来处理就能够解决除数与被除数越界的问题。同时使用倍乘法进行判断时， $x$ 增大一倍之前，需要判断其值是否大于 INT_MAX/2，如果大于此值继续扩大一倍就会导致越界，因此直接返回INT_MIN。

代码

class Solution {
    final int INT_MIN = Integer.MIN_VALUE;
    final int INT_MAX = Integer.MAX_VALUE;
    final int M = INT_MIN / 2;
    public int divide(int a, int b) {
        if (a == INT_MIN && b == -1) return INT_MAX;
        // 判断符号位
        int sign = (a > 0) ^ (b > 0) ? -1 : 1;
        if (a > 0) a = -a;
        if (b > 0) b = -b;
        int res = 0;
        while (a <= b) {
            int value = b;
            int x = 1;
            while (value >= M && a <= value + value) {
                value += value;
                if (x > INT_MAX / 2) return INT_MIN;
                x += x;
            }
            a -= value;
            res += x;
        }
        return sign == 1 ? res : -res;
    }
}

题目 10. 正则表达式匹配

题目难度：龍级！

---

题目描述


前去迎战

来自龙卷的提醒：

龍级的题目，终于有意思起来了 ✪ ω ✪

不难发现 s 串与 p 串的内容匹配，可以根据之前的状态推导而来，可以尝试使用动态规划推导状态转移方程解决。

解题分析

定义状态

对于 $s$ 串中的字母想象为背包的总重量，对于 $p$ 中的字母想象为能够拿取的商品。可以定义布尔类型数组 $dp[i][j]$ 存储对于 $s$ 串中$[0,j-1]$ 位置字符与 $p$ 串中 $[0,i-1]$ 位置字符串的匹配情况。$dp[i+1][j+1]$ 存储对于 $s$ 的$[0,j]$ 子串与 $p$ 的 $[0,i]$ 子串的匹配情况。

状态初始化

• $dp[0][0]$ 则表示 s 与 p 均为空串时匹配状态，自然是能够匹配其值为true。
• 对于 $p$ 为空串， $s$ 为非空串的情况，一定无法匹配，因此初始化为 false，即 $dp[0][1,2,3,...n]=false$
• 对于 $s$ 为空串， $p$ 为非空串的情况，因为*能代表任意个包括 0 个字符，因此两串可能存在匹配，需要单独处理。

状态转移

索引 $i,j$ 分别遍历 $p,s$ 串，分别有下面几种情况来讨论：

情况一：相同字符匹配，即$p[i]==s[j]或s[j]={=}^{\prime }{.}^{\prime }$，如下图所示：

两位字符相同时，当前状态取决于 $i,j$ 前一位的状态，即：$dp[i+1][j+1]|=dp[i][j]$

情况二：通配符*匹配，即$p[i]={=}^{\prime }{\ast }^{\prime }$，如下图所示：*

因为通配符*可以匹配任意次数，因此需要分拿取次数而定：

• 匹配方式一：统配符匹配 0 个字符。

如下图所示，直接忽略通配符与统配符前一个字符 $pre$ ， 此时$dp[i+1][j+1]|=dp[i-1][j+1]$。

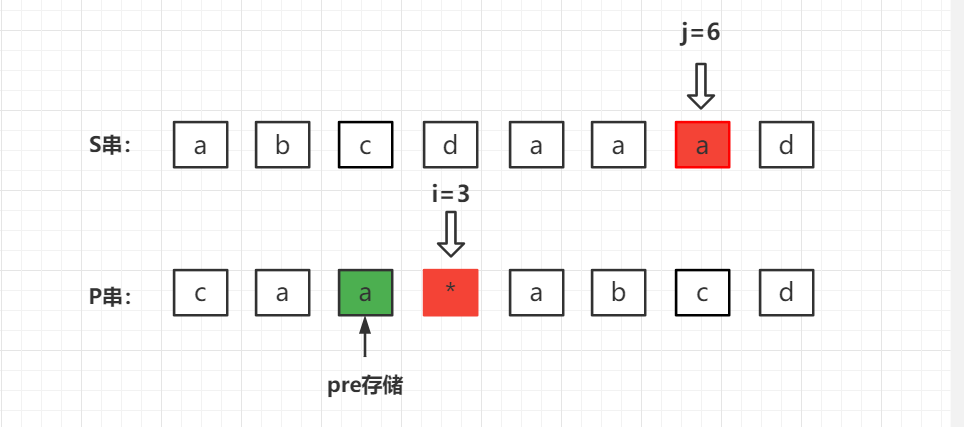
• 匹配方式二：通配符匹配 n 次（n > 0）

既然通配符匹配字符，那么要求 S 串中的对应的位置需要有连续的字符 $pre$ 。那么定义一个变量存储 $j$ 的位置，从右向左扫描 $s[j]$ 的值是否与 $pre$ 相同，如果相同则代表通配符可以进行一次匹配操作；否则停止扫描。

此时使用循环变量$idx$ ，判断$s[idx]==pre$ ，相同则执行 $dp[i+1][j+1]|=dp[i-1][idx]$

• 其余情况

无法匹配也无法统配，$dp[i+1][j+1]=false$

返回结果

最终，$dp[p.length][s.length]$ 存储的值就是两串的正则表达式匹配情况，直接将其返回。

代码(Java代码）

class Solution {
    // 判断传入字符是否匹配
    public boolean equals(char c, char a) {
        return c == a || c == '.' || a == '.';
    }
    public boolean isMatch(String s, String p) {
        int sLen = s.length();
        int pLen = p.length();
        boolean[][] dp = new boolean[pLen + 1][sLen + 1];
        // 开始初始化
        dp[0][0] = true;
        boolean find = false;
        for (int i = 0; i < pLen; ++i) {
            char c = p.charAt(i);
            if (Character.isAlphabetic(c) || c == '.') {
                if (find) {
                    break;
                }
                find = true;
            } else {
                dp[i + 1][0] = true;
                find = false;
            }
        }
        // 记录上一个字符，用于 * 匹配
        char pre = 0;
        for (int i = 0; i < pLen; ++i) {
            char c = p.charAt(i);
            for (int j = 0; j < sLen; ++j) {
                char t = s.charAt(j);
                // *
                if(c == '*') {
                    // 一次都不拿
                    dp[i + 1][j + 1] |= dp[i - 1][j + 1];
                    // 拿取 n 次
                    int idx = j;
                    while (idx >= 0 && equals(s.charAt(idx), pre)) {
                        dp[i + 1][j + 1] |= dp[i - 1][idx];
                        --idx;
                    }
                }
                // 能够匹配(字母或'.')
                else if (equals(c, t)) {
                    dp[i + 1][j + 1] |= dp[i][j];
                }
            }
            pre = c;
        }
        return dp[pLen][sLen];
    }
}

写在最后

好了今天LeetCode好题分享就到这里结束了，最后就用泰戈尔一句诗来收尾吧：

不用徘徊采花保存，只管往前走去，前途上百花自会盛开

感谢你的阅读

---