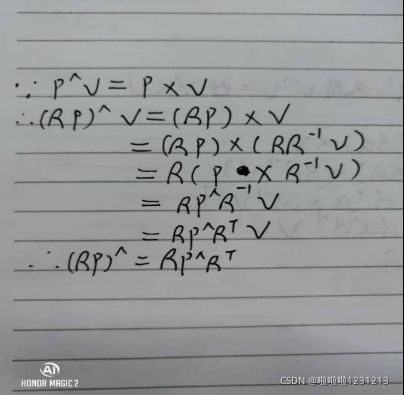视觉slam学习笔记以及课后习题《第三讲李群李代数》

 前言

这篇博客主要记录了我在深蓝学院视觉slam课程中的课后习题，因为是为了统计知识点来方便自己以后查阅，所以有部分知识可能不太严谨，如果给大家造成了困扰请见谅，大家发现了问题也可以私信或者评论给我及时改正，欢迎大家一起探讨。其他章的笔记可以在我的首页文章中查看。

整个作业的代码和文档都可以参考我的GitHub存储库GitHub - 1481588643/vslam

如果想要了解视觉slam其他章节的内容，也可以查阅以下链接

https://blog.csdn.net/m0_61238051/article/details/120603418?spm=1001.2014.3001.5501

视觉slam学习笔记以及课后习题《第二讲三维物体刚体运动》_m0_61238051的博客-CSDN博客

https://blog.csdn.net/m0_61238051/article/details/120813741

一.群的性质 (1 分,约 1 小时)
课上我们讲解了什么是群。请根据群定义,求解以下问题:
1. {Z, +} 是否为群?若是,验证其满足群定义;若不是,说明理由。
2. {N, +} 是否为群?若是,验证其满足群定义;若不是,说明理由。
3. 解释什么是阿贝尔群。并说明矩阵及乘法构成的群是否为阿贝尔群。
其中 Z 为整数集,N 为自然数集。

答：阿贝尔群（Abelian Group），又称交换群或加群，是这样一类群：

它由自身的集合 G 和二元运算 * 构成。它除了满足一般的群公理，即运算的结合律、G 有单位元、所有 G 的元素都有逆元之外，还满足交换律公理。因为阿贝尔群的群运算满足交换律和结合律，群元素乘积的值与乘法运算时的次序无关。

矩阵即使是可逆矩阵，一般不形成在乘法下的阿贝尔群，因为矩阵乘法一般是不可交换的。但是某些矩阵的群是在矩阵乘法下的阿贝尔群 - 一个例子是 2x2 旋转矩阵的群。

三. 验证向量叉乘的李代数性质 (2 分,约 1 小时)
我们说向量和叉乘运算构成了李代数,现在请你验证它。书中对李代数的定义为:李代数由一个集合
V,一个数域 F 和一个二元运算 [, ] 组成。如果它们满足以下几条性质,称 (V, F, [, ]) 为一个李代数,记作
g。
1. 封闭性 ∀X, Y ∈ V, [X, Y ] ∈ V.
2. 双线性 ∀X, Y , Z ∈ V, a, b ∈ F, 有:
[aX + bY , Z] = a[X, Z] + b[Y , Z],
3. 自反性 1
[Z, aX + bY ] = a[Z, X] + b[Z, Y ].
∀X ∈ V, [X, X] = 0.
4. 雅可比等价
∀X, Y , Z ∈ V, [X, [Y , Z]] + [Y , [Z, X]] + [Z, [X, Y ]] = 0.
其中二元运算被称为李括号。
现取集合 V = R 3 ,数域 F = R,李括号为:
[a, b] = a × b.
请验证 g = (R 3 , R, ×) 构成李代数。

 三. 推导 SE(3) 的指数映射 (1 分,约 1 小时)

 四.伴随 (2 分,约 1 小时)

 五.常见函数的求导应用 (2 分,约 2 小时)

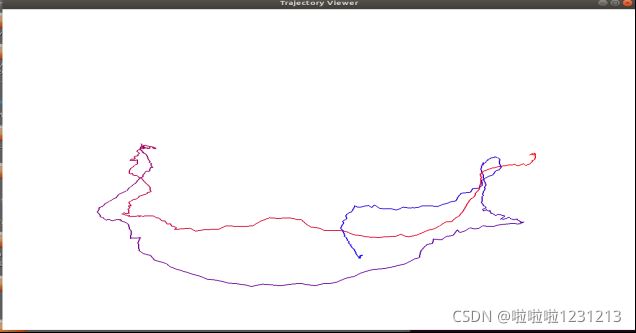
六. 轨迹的描绘 (2 分,约 1 小时)
我们通常会记录机器人的运动轨迹,来观察它的运动是否符合预期。大部分数据集都会提供标准轨迹
以供参考,如 kitti、TUM-RGBD 等。这些文件会有各自的格式,但首先你要理解它的内容。记世界坐标
系为 W ,机器人坐标系为 C,那么机器人的运动可以用 T W C 或 T CW 来描述。现在,我们希望画出机器
人在世界当中的运动轨迹,请回答以下问题:
1. 事实上,T W C 的平移部分即构成了机器人的轨迹。它的物理意义是什么?为何画出 T W C 的平移
部分就得到了机器人的轨迹?
2. 我为你准备了一个轨迹文件(code/trajectory.txt)。该文件的每一行由若干个数据组成,格式为
[t, t x , t y , t z , q x , q y , q z , q w ],
其中 t 为时间,t x , t y , t z 为 T W C 的平移部分,q x , q y , q z , q w 是四元数表示的 T W C 的旋转部分,q w
为四元数实部。同时,我为你提供了画图程序 draw_trajectory.cpp 文件。该文件提供了画图部分
的代码,请你完成数据读取部分的代码,然后书写 CMakeLists.txt 以让此程序运行起来。注意我
们需要用到 Pangolin 库来画图,所以你需要事先安装 Pangolin(如果你做了第一次作业,那么现
在已经安装了)。CMakeLists.txt 可以参照 ORB-SLAM2 部分。 

#include 
#include 
#include 
#include 

#include 
#include 

// need pangolin for plotting trajectory
#include 

using namespace std;

// path to trajectory file
string trajectory_file = "../trajectory.txt";

// function for plotting trajectory, don't edit this code
// start point is red and end point is blue
void DrawTrajectory(vector>);

int main(int argc, char **argv) {

    vector> poses;

    /// implement pose reading code
    // start your code here (5~10 lines)
    ifstream f_str(trajectory_file);

    if (!f_str)
    {
        cout << "cannot find the file of trajectory at: " << trajectory_file << endl;
        return 1;
    }

    while(!f_str.eof()) //end of file
    {
        double time, tx, ty, tz, qx, qy, qz, w;
        f_str >> time >> tx >> ty >> tz >> qx >> qy >> qz >> w;
        Eigen::Quaterniond q= Eigen::Quaterniond(w, qx, qy, qz).normalized();
        Eigen::Vector3d t(tx, ty, tz);
        Sophus::SE3d SE3_qt(q, t);
        poses.push_back(SE3_qt);
    }
    cout << "complete it! read total: " << poses.size() << endl;
    // end your code here

    // draw trajectory in pangolin
    DrawTrajectory(poses);
    return 0;
}

void DrawTrajectory(vector> poses) {
    if (poses.empty()) {
        cerr << "Trajectory is empty!" << endl;
        return;
    }

    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));


    while (!pangolin::ShouldQuit()) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

        glLineWidth(2);
        for (size_t i = 0; i < poses.size() - 1; i++) {
            glColor3f(1 - (float) i / poses.size(), 0.0f, (float) i / poses.size());
            glBegin(GL_LINES);
            auto p1 = poses[i], p2 = poses[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }
        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }

}

 

 七.* 轨迹的误差 (2 分,约 1 小时)

#include 
#include 
#include 
#include 
#include 

using namespace Sophus;
using namespace std;

string groundtruth_file = "../groundtruth.txt";
string estimated_file = "../estimated.txt";

typedef vector> TrajectoryType;

void DrawTrajectory(const TrajectoryType >, const TrajectoryType &esti);

TrajectoryType ReadTrajectory(const string &path);

int main(int argc, char **argv) {
  TrajectoryType groundtruth = ReadTrajectory(groundtruth_file);
  TrajectoryType estimated = ReadTrajectory(estimated_file);
  assert(!groundtruth.empty() && !estimated.empty());
  assert(groundtruth.size() == estimated.size());

  // compute rmse
  double rmse = 0;
  for (size_t i = 0; i < estimated.size(); i++) {
    Sophus::SE3d p1 = estimated[i], p2 = groundtruth[i];
    double error = (p2.inverse() * p1).log().norm();
    rmse += error * error;
  }
  rmse = rmse / double(estimated.size());
  rmse = sqrt(rmse);
  cout << "RMSE = " << rmse << endl;

  DrawTrajectory(groundtruth, estimated);
  return 0;
}

TrajectoryType ReadTrajectory(const string &path) {
  ifstream fin(path);
  TrajectoryType trajectory;
  if (!fin) {
    cerr << "trajectory " << path << " not found." << endl;
    return trajectory;
  }

  while (!fin.eof()) {
    double time, tx, ty, tz, qx, qy, qz, qw;
    fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
    Sophus::SE3d p1(Eigen::Quaterniond(qw, qx, qy, qz), Eigen::Vector3d(tx, ty, tz));
    trajectory.push_back(p1);
  }
  return trajectory;
}

void DrawTrajectory(const TrajectoryType >, const TrajectoryType &esti) {
  // create pangolin window and plot the trajectory
  pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
  glEnable(GL_DEPTH_TEST);
  glEnable(GL_BLEND);
  glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

  pangolin::OpenGlRenderState s_cam(
      pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
      pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
  );

  pangolin::View &d_cam = pangolin::CreateDisplay()
      .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
      .SetHandler(new pangolin::Handler3D(s_cam));


  while (pangolin::ShouldQuit() == false) {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    d_cam.Activate(s_cam);
    glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

    glLineWidth(2);
    for (size_t i = 0; i < gt.size() - 1; i++) {
      glColor3f(0.0f, 0.0f, 1.0f);  // blue for ground truth
      glBegin(GL_LINES);
      auto p1 = gt[i], p2 = gt[i + 1];
      glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
      glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
      glEnd();
    }

    for (size_t i = 0; i < esti.size() - 1; i++) {
      glColor3f(1.0f, 0.0f, 0.0f);  // red for estimated
      glBegin(GL_LINES);
      auto p1 = esti[i], p2 = esti[i + 1];
      glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
      glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
      glEnd();
    }
    pangolin::FinishFrame();
    usleep(5000);   // sleep 5 ms
  }

}