数据科学分布——Beta分布

概念

贝塔分布（Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，在机器学习和数理统计学中有重要应用。在概率论中，贝塔分布，也称Β分布，是指一组定义在(0,1) 区间的连续概率分布。

可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

# 加载功能包
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML

# 指定大小
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams['figure.figsize']=(14,7)
plt.figure(dpi=100)

# PDF 概率密度函数
plt.plot(np.linspace(0,1,100),stats.beta.pdf(np.linspace(0,1,100),a=2,b=2))
print(stats.beta.pdf(np.linspace(0,1,100),a=2,b=2))
# linspace选择取值；beta分布
plt.fill_between(np.linspace(0,1,100),stats.beta.pdf(np.linspace(0,1,100),a=2,b=2),alpha=.45,)
# 进行图像填充

# CDF累计概率密度函数
plt.plot(np.linspace(0,1,100),stats.beta.cdf(np.linspace(0,1,100),a=2,b=2))

# 补充图设置：LEGEND、TICKS与TITLE
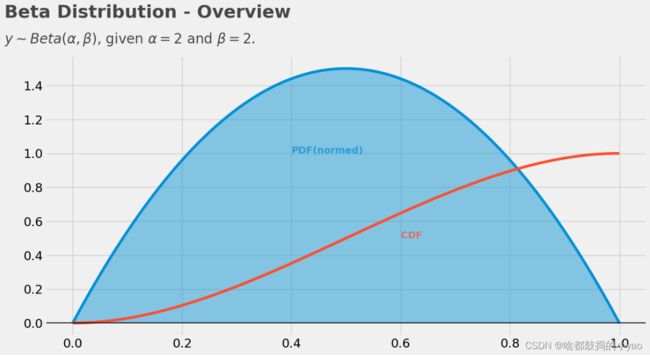
plt.text(x=.4, y=1, s="PDF(normed)", alpha = 75, weight="bold", color="#008fd5")
plt.text(x=0.6, y=0.5, s="CDF", alpha = 75, weight="bold", color="#fc4f30")
plt.tick_params(axis = 'both', which ='major', labelsize = 18)
plt.axhline(y = 0, color ='black', linewidth = 1.3, alpha = 7)
plt.text(x = -.125, y = 1.8, s = "Beta Distribution - Overview", fontsize = 26, weight = 'bold', alpha = 75)
plt.text(x = -.125, y = 1.65, s = "$y \\sim Beta(\\alpha,\\beta)$, given $ \\alpha = 2 $ and $ \\beta = 2$. ", fontsize = 20, alpha = 75)

[0. 0.05999388 0.11876339 0.17630854 0.23262932 0.28772574
0.3415978 0.39424549 0.44566881 0.49586777 0.54484236 0.59259259
0.63911846 0.68441996 0.72849709 0.77134986 0.81297827 0.85338231
0.89256198 0.93051729 0.96724824 1.00275482 1.03703704 1.07009489
1.10192837 1.1325375 1.16192225 1.19008264 1.21701867 1.24273033
1.26721763 1.29048056 1.31251913 1.33333333 1.35292317 1.37128864
1.38842975 1.4043465 1.41903887 1.43250689 1.44475054 1.45576982
1.46556474 1.47413529 1.48148148 1.48760331 1.49250077 1.49617386
1.49862259 1.49984695 1.49984695 1.49862259 1.49617386 1.49250077
1.48760331 1.48148148 1.47413529 1.46556474 1.45576982 1.44475054
1.43250689 1.41903887 1.4043465 1.38842975 1.37128864 1.35292317
1.33333333 1.31251913 1.29048056 1.26721763 1.24273033 1.21701867
1.19008264 1.16192225 1.1325375 1.10192837 1.07009489 1.03703704
1.00275482 0.96724824 0.93051729 0.89256198 0.85338231 0.81297827
0.77134986 0.72849709 0.68441996 0.63911846 0.59259259 0.54484236
0.49586777 0.44566881 0.39424549 0.3415978 0.28772574 0.23262932
0.17630854 0.11876339 0.05999388 0. ]

参数影响

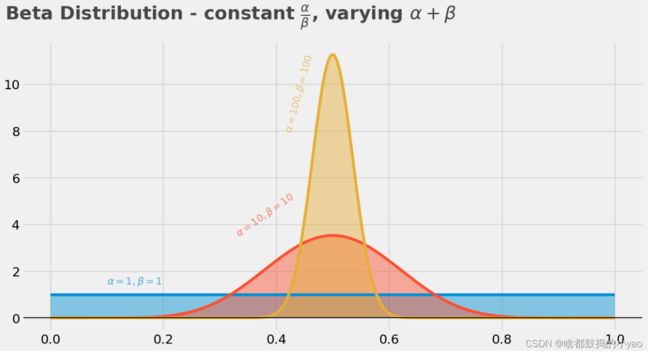
数量

plt.figure(dpi=100)
#a是成功次数、b是失败次数

# PDF A=B=1
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=1,b=1))
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=1,b=1),alpha=.45,)

# PDF A=B=10
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=10,b=10))
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=10,b=10),alpha=.45,)

# PDF A=B=100
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=100,b=100))
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=100,b=100),alpha=.45,)

# LEGEND TICKS TITLE
plt.text(x=.1, y=1.45, s=r"$ \alpha = 1, \beta = 1 $", alpha = 75, weight="bold", color="#008fd5")
plt.text(x=0.325, y=3.5, s=r"$ \alpha = 10, \beta = 10 $", rotation=35, alpha = 75, weight="bold", color="#fc4f30")
plt.text(x=.4125, y=8, s=r"$ \alpha = 100, \beta = 100 $", rotation=75, alpha = 75, weight="bold", color="#e5ae38")
plt.tick_params(axis = 'both', which ='major', labelsize = 18)
plt.axhline(y = 0, color ='black', linewidth = 1.3, alpha = 7)
plt.text(x = -.08, y = 12.75, s = r"Beta Distribution - constant $ \frac{\alpha}{\beta} $, varying $\alpha+\beta$", fontsize = 26, weight = 'bold', alpha = 75)

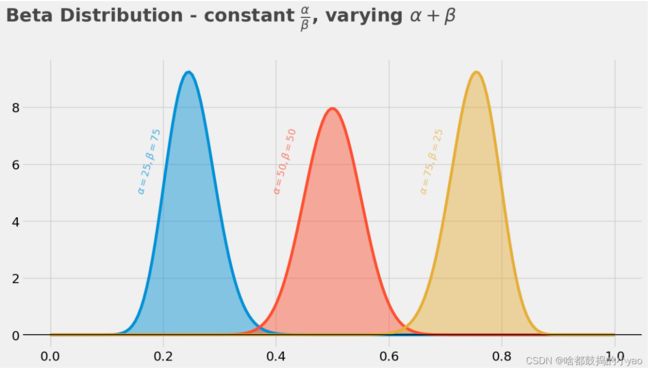
比例

plt.figure(dpi=100)
#a是成功次数：1、b是失败次数：0

# PDF A/B=1/3
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=25,b=75))
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=25,b=75),alpha=.45,)

# PDF A/B=1
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=50,b=50))
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=50,b=50),alpha=.45,)

# PDF A/B=3
plt.plot(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=75,b=25))
plt.fill_between(np.linspace(0,1,200),stats.beta.pdf(np.linspace(0,1,200),a=75,b=25),alpha=.45,)

# LEGEND TICKS TITLE
plt.text(x=.15, y=5, s=r"$ \alpha = 25, \beta = 75 $", rotation=75, alpha = 75, weight="bold", color="#008fd5")
plt.text(x=0.39, y=5, s=r"$ \alpha = 50, \beta = 50 $", rotation=75, alpha = 75, weight="bold", color="#fc4f30")
plt.text(x=.65, y=5, s=r"$ \alpha = 75, \beta = 25 $", rotation=75, alpha = 75, weight="bold", color="#e5ae38")
plt.tick_params(axis = 'both', which ='major', labelsize = 18)
plt.axhline(y = 0, color ='black', linewidth = 1.3, alpha = 7)
plt.text(x = -.08, y = 11, s = r"Beta Distribution - constant $ \frac{\alpha}{\beta} $, varying $\alpha+\beta$", fontsize = 26, weight = 'bold', alpha = 75)

随机产生数据

from scipy.stats import beta

# draw a single sample
print(beta.rvs(a=2,b=2),end="\n\n")

# draw 10 samples
print(beta.rvs(a=2,b=2,size=10), end="\n\n")

0.39008533097914994

[0.29036031 0.81142835 0.55814129 0.56748235 0.47717343 0.90101806
0.58081651 0.72243883 0.91436309 0.15177402]

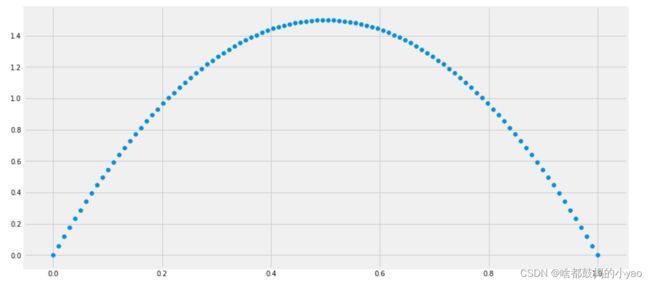
概率密度函数

from scipy.stats import beta

# additional imoprts for plotting purpose
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"] = (14,7)

# continuous pdf for the plot
x_s = np.linspace(0,1,100)
y_s = beta.pdf(a=2,b=2,x=x_s)
plt.scatter(x_s, y_s);

累积概率密度函数

from scipy.stats import beta

# probabolity of x less or equal 0.3
print("P(X<0.3)={:.3}".format(beta.cdf(a=2,b=2,x=0.3)))

# probability of x in [-0.2, +0.2]
print("P(-0.2.format(beta.cdf(a=2,b=2,x=0.2)-beta.cdf(a=2,b=2,x=-0.2)))

P(X<0.3)=0.216
P(-0.2