tensorflow实验四----波士顿房价预测

波士顿房价预测

波士顿房价数据集包括506个样本，每个样本包括12个特征变量和该地区的平均房价房价（单价）显然和多个特征变量相关，不是单变量线性回归（一元线性回归）问题选择多个特征变量来建立线性方程，这就是多变量线性回归（多元线性回归）问题波士顿房价预测

数据集解读、

CRIM: 城镇人均犯罪率
ZN：住宅用地超过25000 sq.ft. 的比例
INDUS: 城镇非零售商用土地的比例
CHAS: 边界是河流为1，否则0
NOX: 一氧化氮浓度
RM: 住宅平均房间数数据集解读
AGE: 1940年之前建成的自用房屋比例
DIS：到波士顿5个中心区域的加权距离
RAD:辐射性公路的靠近指数
TAX : 每10000美元的全值财产税率
PTRATIO: 城镇师生比例
LSTAT: 人口中地位低下者的比例
MEDV: 自住房的平均房价，单位：千美元

读取数据

import tensorflow.compat.v1 as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
from sklearn.utils import shuffle
from sklearn.preprocessing import scale
print("Tensorflow版本是：",tf.__version__)

通过Pandas导入数据

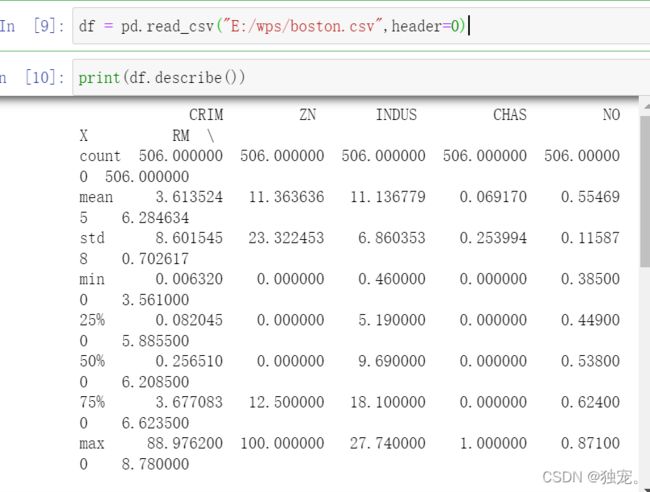
df = pd.read_csv("E:/wps/boston.csv",header=0)  #这里的路径就是你存放波士顿房价文件的绝对路径
print(df.describe())

Pandas读取数据
显示前三条数据

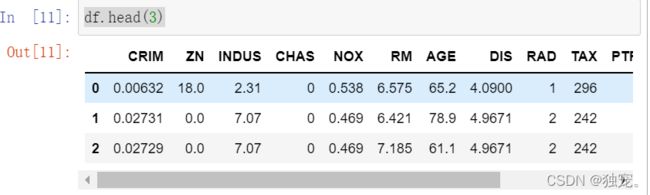
df.head(3)

显示后三条数据

df.tail(3)

数据集划分

数据准备

ds = df.values
print(ds.shape)
print(ds)

划分特征数据和标签数据

x_data = ds[:,:12]
y_data = ds[:,12]

print('x_data shape=',x_data.shape)
print('y_data shape=',y_data.shape)

划分训练集、验证集和测试集

train_num = 300
valid_num = 100
test_num = len(x_data) - train_num -valid_num

x_train =x_data[:train_num]
y_train =y_data[:train_num]

x_valid = x_data[train_num:train_num+valid_num]
y_valid = y_data[train_num:train_num+valid_num]

x_test = x_data[train_num+valid_num:train_num+valid_num+test_num]
y_test = y_data[train_num+valid_num:train_num+valid_num+test_num]

转换数据类型

x_train = tf.cast(scale(x_train),dtype=tf.float32)
x_valid = tf.cast(scale(x_valid),dtype=tf.float32)
x_test = tf.cast(scale(x_test),dtype=tf.float32)

注意这里有一个情况，这里使用来一个scale()函数，如果不适用这个函数会导致训练结果异常，会出现下图的情况，train_loss和valid_loss都没有值

构建模型

定义模型

多元线性回归模型仍然是个简单的线性函数，其基本形式还是=∗+，只是此处和不再是一个标量，形状会不同。根据模型定义，执行的是矩阵叉乘，所以此处调用的是tf.matmul()函数。

def model(x,w,b):
    return tf.matmul(x,w) + b

创建待优化变量

W = tf.Variable(tf.random.normal([12,1],mean=0.0,stddev=1.0,dtype=tf.float32))
B = tf.Variable(tf.zeros(1),dtype = tf.float32)
print(W)
print(B)

模型训练

设置超参数
本列将采用小批量梯度下降算法MBGD进行优化

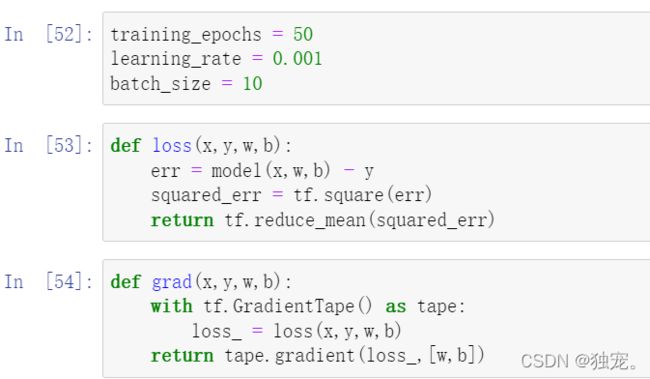
training_epochs = 50
learning_rate = 0.001
batch_size = 10

设置了一个batch_size超参数，用来调整每次进行小批量训练优化的样本数

定义均方差损失函数

def loss(x,y,w,b):
    err = model(x,w,b) - y
    squared_err = tf.square(err)
    return tf.reduce_mean(squared_err)

定义梯度计算函数

def grad(x,y,w,b):
    with tf.GradientTape() as tape:
        loss_ = loss(x,y,w,b)
    return tape.gradient(loss_,[w,b])

选择优化器

optimizer = tf.keras.optimizers.SGD(learning_rate)

使用tf.keras.optimizers.SGD()声明了一个梯度下降优化器（Optimizer），其学习率通过参数指定。优化器可以帮助根据计算出的求导结果更新模型参数，从而最小化损失函数，具体使用方式是调用其apply_gradients()方法。

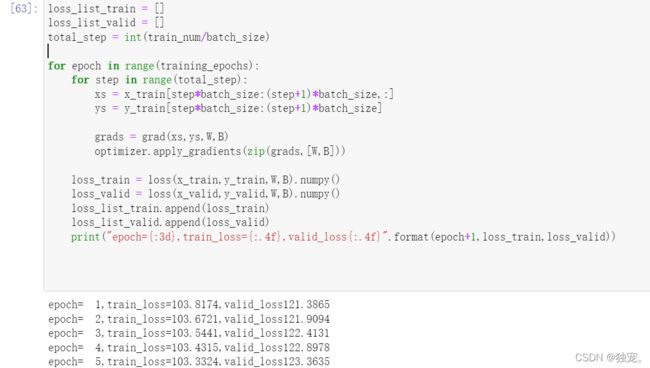
迭代训练

loss_list_train = []
loss_list_valid = []
total_step = int(train_num/batch_size)

for epoch in range(training_epochs):
    for step in range(total_step):
        xs = x_train[step*batch_size:(step+1)*batch_size,:]
        ys = y_train[step*batch_size:(step+1)*batch_size]
        
        grads = grad(xs,ys,W,B)
        optimizer.apply_gradients(zip(grads,[W,B]))
        
    loss_train = loss(x_train,y_train,W,B).numpy()
    loss_valid = loss(x_valid,y_valid,W,B).numpy()
    loss_list_train.append(loss_train)
    loss_list_valid.append(loss_valid)
    print("epoch={:3d},train_loss{:.4f},valid_loss{:.4f}".format(epoch+1,loss_train,loss_valid)        

这样操作train_loss 和valid_loss的值就都有了

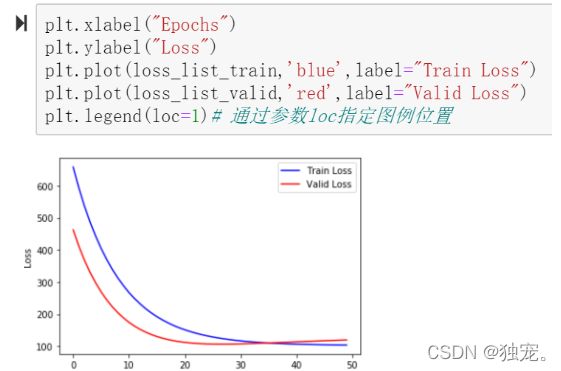
可视化损失值

plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.plot(loss_list_train,'blue',label="Train Loss")
plt.plot(loss_list_valid,'red',label='Valid Loss')
plt.legend(loc=1)

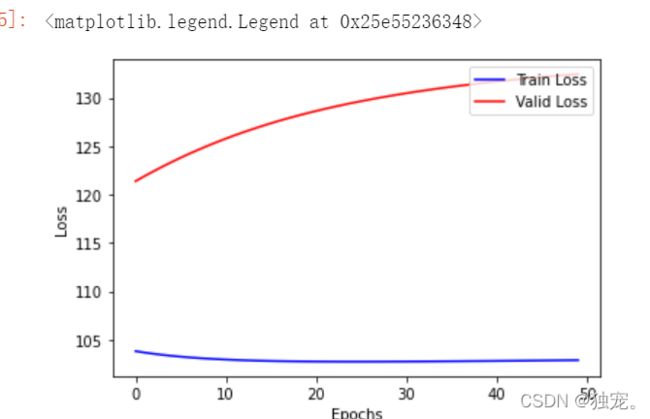
这里注意执行的次数越多，损失值越大，两条线的距离就越大，比如下图

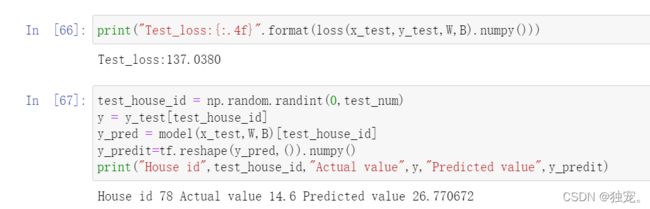
查看测试集的损失

print("Test_loss:{:.4f}".format(loss(x_test,y_test,W,B).numpy()))

测试集里随机选一条

test_house_id = np.random.randint(0,test_num)
y = y_test[test_house_id]
y_pred = model(x_test,W,B)[test_house_id]
y_predit=tf.reshape(y_pred,()).numpy()
print("House id",test_house_id,"Actual value",y,"Predicted value",y_predit)

这样就完成了！！！