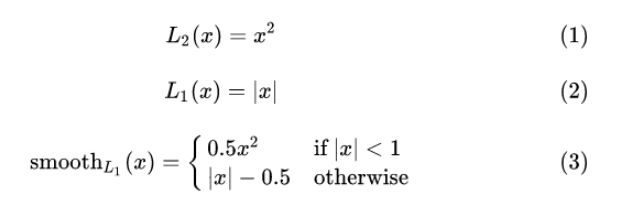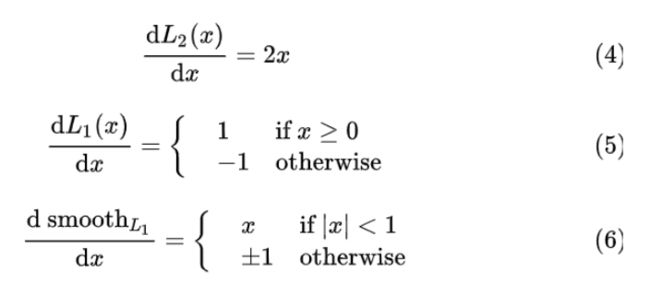Fast R-CNN论文详解

Fast R-CNN详解

---

---

1.RCNN回顾

RCNN算法分为4个步骤：

1. 候选区域生成： 一张图像生成1K~2K个候选区域 （采用Selective Search 方法）
2. 特征提取： 对每个候选区域，使用深度卷积网络提取特征 （CNN）
3. 类别判断： 特征送入每一类的SVM 分类器，判别是否属于该类
4. 位置精修： 使用回归器精细修正候选框位置

1.1 Fast RCNN主要贡献点

1. 实现大部分end-to-end训练(提proposal阶段除外)： 所有的特征都暂存在显存中，就不需要额外的磁盘空间,joint training （SVM分类，bbox回归 联合起来在CNN阶段训练）把最后一层的Softmax换成两个，一个是对区域的分类Softmax（包括背景），另一个是对bounding box的微调。这个网络有两个输入，一个是整张图片，另一个是候选proposals算法产生的可能proposals的坐标。（对于SVM和Softmax，论文在SVM和Softmax的对比实验中说明，SVM的优势并不明显，故直接用Softmax将整个网络整合训练更好。对于联合训练： 同时利用了分类的监督信息和回归的监督信息，使得网络训练的更加鲁棒，效果更好。这两种信息是可以有效联合的。）

2. 提出了一个RoI层，算是SPP的变种，SPP是pooling成多个固定尺度，RoI只pooling到单个固定的尺度 （论文通过实验得到的结论是多尺度学习能提高一点点mAP，不过计算量成倍的增加，故单尺度训练的效果更好。）

3. 指出SPP-net训练时的不足之处，并提出新的训练方式，就是把同张图片的prososals作为一批进行学习，而proposals的坐标直接映射到conv5层上，这样相当于一个batch一张图片的所以训练样本只卷积了一次。文章提出他们通过这样的训练方式或许存在不收敛的情况，不过实验发现，这种情况并没有发生。这样加快了训练速度。 （实际训练时，一个batch训练两张图片，每张图片训练64个RoIs（Region of Interest））

   ---

2.Fast RCNN算法框架

首先Fast RCNN相比于RCNN主要在以下方面进行了改进:

1. Fast RCNN仍然使用selective search选取2000个建议框，但是这里不是将这么多建议框都输入卷积网络中，而是将原始图片输入卷积网络中得到特征图，再使用建议框对特征图提取特征框。这样做的好处是，原来建议框重合部分非常多，卷积重复计算严重，而这里每个位置都只计算了一次卷积，大大减少了计算量
2. 由于建议框大小不一，得到的特征框需要转化为相同大小，这一步是通过ROI池化层来实现的（ROI表示region of interest即目标）
3. Fast RCNN里没有SVM分类器和回归器了，分类和预测框的位置大小都是通过卷积神经网络输出的
4. 为了提高计算速度，网络最后使用SVD代替全连接层

使用Fast RCNN进行目标检测的预测流程如下:

1. 拿到一张图片，使用selective search选取建议框
2. 将原始图片输入卷积神经网络之中，获取特征图（最后一次池化前的卷积计算结果）
3. 对每个建议框，从特征图中找到对应位置（按照比例寻找即可），截取出特征框（深度保持不变）
4. ROI池化，将每个特征框划分为$H\times W$个网格（论文中是$7\times 7$），在每个网格内进行池化（即每个网格内取最大值）。这样每个特征框就被转化为了$7\times 7\times C$ 的矩阵(其中C为深度)
5. 对每个矩阵拉长为一个向量，分别作为之后的全连接层的输入
6. 全连接层的输出有两个，计算分类得分和bounding box回归（bounding box表示预测时要画的框）。前者是sotfmax的21类分类器（有20个类别+背景类），输出属于每一类的概率（所有建议框的输出构成得分矩阵）；后者是输出一个$20\times 4$的矩阵，$4表示(x,y,w,h)$，$20表示20$个类，这里是对$20$个类分别计算了框的位置和大小
7. 对输出的得分矩阵使用非极大抑制方法抑制剔除重叠建议框，对每一个框选择概率最大的类作为标注的类，最终得到每个类别中回归修正后的得分最高的窗口

---

3.训练过程

3.1 详细步骤

论文中使用了多种网络结构进行训练，这里以VGG-16（AlexNet之后的又一经典网络）为例。

最开始仍然是在ImageNet数据集上训练一个1000类的分类网络

然后对模型进行“三个变动”

• 将最后一个最大池化层换成ROI池化层
• 将最后一个全连接层和后面的softmax 1000分类器换成两个并行层，前者是分类的输出，代表每个region proposal属于每个类别（21类）的得分，后者是回归的输出，代表每个region proposal的四个坐标
• 输入的不再只是图片，还有提取到的建议框位置信息

变化后的模型结构如下所示

使用变动后的模型，在标注过的图像数据上继续训练，训练时要输入图像、标注（这里将人为标注的框称为ground truth）和建议框信息。这里为了提高训练速度，采取了小批量梯度下降的方式，每次使用2张图片的128张建议框（每张图片取64个建议框）更新参数。

每次更新参数的训练步骤如下

• 2张图像直接经过前面的卷积层获得特征图
• 根据ground truth标注所有建议框的类别。具体步骤为，对每一个类别的ground truth，与它的IoU大于0.5的建议框标记为groud truth的类别，对于与ground truth的iou介于0.1到0.5之间的建议框，标注为背景类别
• 每张图片随机选取64个建议框（要控制背景类的建议框占75%），提取出特征框
• 特征框继续向下计算，进入两个并行层计算损失函数（损失函数具体计算见下面）
• 反向传播更新参数（关于ROI池化的反向传播细节可以参考这篇博客）

3.2 训练过程图解

训练数据构成

N张完整图片以50%概率水平翻转。

R个候选框的构成方式如下：

类别	比例	方式
前景	25%	与某个真值重叠在[0.5,1]的候选框
背景	75%	与真值重叠的最大值在[0.1,0.5)的候选框

---

4.ROI池化

我们知道在ImageNet数据上做图片分类的网络，一般都是先把图片crop、resize到固定的大小（224*224），然后输入网络提取特征再进行分类，而对于检测任务这个方法显然并不适合，因为原始图像如果缩小到224这种分辨率，那么感兴趣对象可能都会变的太小无法辨认。RCNN的数据输入和SPPNet有点类似，并不对图片大小限制，而实现这一点的关键所在，就是ROI Pooling网络层，它可以在任意大小的图片feature map上针对输入的每一个ROI区域提取出固定维度的特征表示，保证后续对每个区域的后续分类能够正常进行。

与SPP的目的相同：如何把不同尺寸的ROI映射为固定大小的特征。ROI就是特殊的SPP，只不过它没有考虑多个空间尺度，只用单个尺度（下图只是大致示意图）。

ROI Pooling的具体实现可以看做是针对ROI区域的普通整个图像feature map的Pooling，只不过因为不是固定尺寸的输入，因此每次的pooling网格大小得手动计算，比如某个ROI区域坐标为$(x1,y1,x2,y2)$，那么输入size为$(y2-y1)\cdot (x2-x1)$ ，如果pooling的输出size为 $poole{d}_{height}\cdot poole{d}_{width}$，那么每个网格的size为$((y2-y1)/poole{d}_{height}\cdot (x2-x1)/poole{d}_{width})$。

---

5.损失函数

损失函数分为两个部分，分别对应两个并行层

• 对类别输出按照softmax正常计算损失
• 对框的位置的损失方面，标注为背景类的建议框不增加损失（体现在下面公式中的$1[u>1]$ ，其实背景类直接不需要计算框的位置这一层损失）。对于标注为物体类别的建议框来说，因为这一层输出的是每一个类别对应的$(x,y,w,h)$，因此需要先挑选出真实类别的四个值，分别与ground truth的四个作差来计算loss

总损失如下：

$$L(p,u,t^u,v)=L_{cls}(p,u)+\lambda [u\ge 1]L_{loc}(t^u,v)$$

损失函数分为两个部分：$L_{cls}$ 表示分类损失，$L_{loc}$ 表示定位损失(回归损失)

$\lambda$用于判断背景，如果分类不是背景，$\lambda =1$

分类如果是背景$\lambda =0$，则不考虑定位损失,即：

分类损失：

对于分类的全连接神经网络，它将产生由Softmax产生的概率$p=(p0,p1...,pK)$。这里K=20,所以共有21个概率值。

$L_{cls}(p,u)=-log(p_u)$，其中$P_u$是真实类型预测的那个概率。也就是说这里只计算一个 ，其他概率值不算。

定位损失：

对于bounding-box回归的全连接网络，它产生的是位置信息$(x,y,w,h)$，分类神经网络每一个概率值，它都对应有一个位置信息。所以网络最后输出维度为：$21\ast 4=84。$

有了ROI Pooling层其实就可以完成最简单粗暴的深度对象检测了，也就是先用selective search等proposal提取算法得到一批box坐标，然后输入网络对每个box包含一个对象进行预测，此时，神经网络依然仅仅是一个图片分类的工具而已，只不过不是整图分类，而是ROI区域的分类，显然大家不会就此满足，那么，能不能把输入的box坐标也放到深度神经网络里然后进行一些优化呢？。

在Fast-RCNN中，有两个输出层：第一个是针对每个ROI区域的分类概率预测 $p=(p0,p1,\cdot \cdot \cdot ,pK)$，第二个则是针对每个ROI区域坐标的偏移优化$t_k=(t_x^k,t_y^k,t_w^k,t_h^k)$,0 ≤ k ≤ K 是多类检测的类别序号。

假设对于类别$k^{\ast }$，在图片中标注了一个ground truth 坐标：$t^{\ast }=(t_x^{\ast },t_y^{\ast },t_w^{\ast },t_h^{\ast })$，而预测值为$t=(t_x,t_y,t_w,t_h)$，二者理论上越接近越好，这里定义损失函数：

这里，$smoot{h}_{L1}(x)$中的x即为$t_i-t_i^{\ast }$即对应坐标的差距。该函数在 (−1,1) 之间为二次函数，而其他区域为线性函数，作者表示这种形式可以增强模型对异常数据的鲁棒性，整个函数在matplotlib中画出来是这样的

---

6.SVD加速

分类和位置调整都是通过全连接层实现的，假设全连接层参数为$W$，尺寸$u\times v$一次前向传播即为：$Y=Wx$ ,计算复次数为$u\times v$

从上图可以看出，两个全连接层（fc6、fc7）占用了44.9%的时间，非常消耗时间。

为此，论文中对W进行SVD分解，并用前t个特征值近似：

$W=U\sum V^T\approx U(:,1:t)\cdot \sum (1:t,1:t)\cdot V(:,1:t{)}^T$

原来的前向传播分解成两步:$y=Wx=U\cdot (\sum \cdot V^T)\cdot x=U\cdot z$

计算复杂度变为$u\times t+v\times t=(u+v)\times t$

在实现时，相当于把一个全连接层拆分成两个，中间以一个低维数据相连。

使用SVD加速后，各部分使用时间如下所示：

7.测试过程

7.1模型在各种数据集上的测试效果及对比

训练数据越多越好吗？

文中分别在VOC 2007、VOC 2010、VOC 2012测试集上测试，发现训练数据越多，效果确实更好。这里微调时采用100k次迭代，每40k次迭代学习率都缩小10倍。

SPPnet论文中采用ZFnet【AlexNet的改进版】这样的小网络，其在微调阶段仅对全连接层进行微调，就足以保证较高的精度，作者文中采用VGG-16【L for large】网路，若仅仅只对全连接层进行微调，mAP会从66.9%降低到61.4%， 所以文中也需要对RoI池化层之前的卷积层进行微调；

那么问题来了？向前微调多少层呢？所有的卷积层都需要微调吗？
作者经过实验发现仅需要对conv3_1及以后卷积层【即9-13号卷积层】进行微调，才使得mAP、训练速度、训练时GPU占用显存三个量得以权衡；
作者说明所有AlexNet【S for small】、VGG_CNN_M_1024【M for medium】的实验结果都是从conv2往后微调，所有VGG-16【L for large】的实验结果都是从conv3_1往后微调。

• 在迁移学习基础上更新哪些层的参数实验

• 直接输出两个层是否真的有优势，SVM V.S. softmax，输入多种规格的图片，更多训练数据等等

  ---

8.smooth L1 loss详解

smooth L1 loss从两个方面限制梯度

• 当预测框与 ground truth 差别过大时，梯度值不至于过大；
• 当预测框与 ground truth 差别很小时，梯度值足够小。

考察如下几种损失函数，其中:

损失函数对 x 的导数分别为：

从（4）中可以看出，当x增大时，L2损失对x的导数也增大。这就导致训练初期，预测值与 groud truth 差异过于大时，损失函数对预测值的梯度十分大，训练不稳定。

从（5）中可以看出，L1 对 x 的导数为常数。这就导致训练后期，预测值与 ground truth 差异很小时， L1 损失对预测值的导数的绝对值仍然为 1，而 learning rate 如果不变，损失函数将在稳定值附近波动，难以继续收敛以达到更高精度。

从（6）中可以看出，smooth L1 在 x 较小时，对 x 的梯度也会变小，而在 x 很大时，对 x 的梯度的绝对值达到上限 1，也不会太大以至于破坏网络参数。 smooth L1 完美地避开了 L1 和 L2 损失的缺陷。其函数图像如下：

由图中可以看出，它在远离坐标原点处，图像和 L1 loss 很接近，而在坐标原点附近，转折十分平滑，不像 L1 loss 有个尖角，因此叫做 smooth L1 loss。

---

[本文整理于B站，知乎，CSDN]
欢迎各位点赞评论收藏⭐️