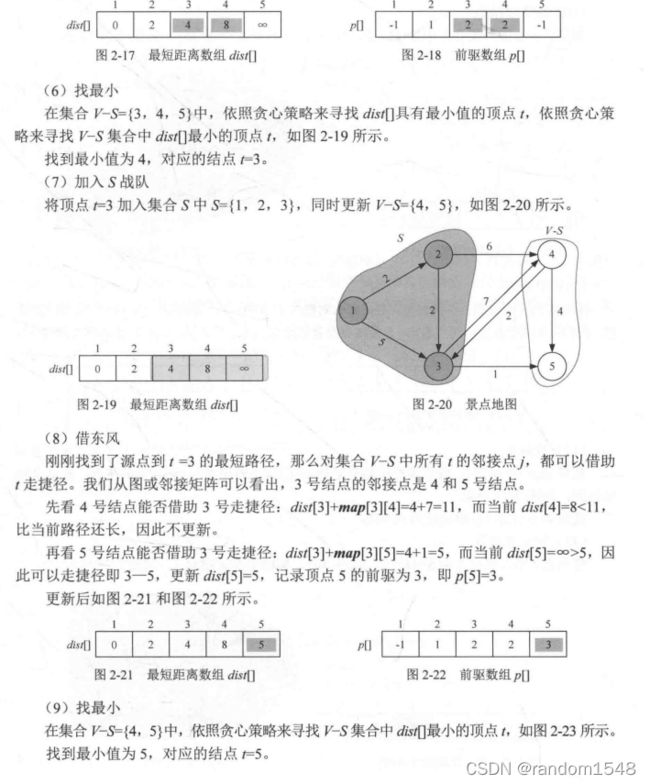
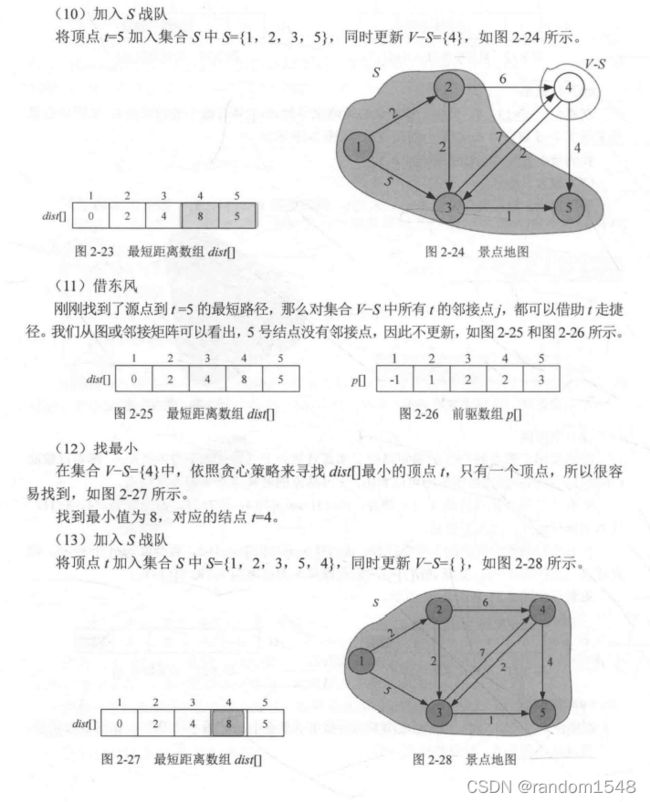
基于Dijkstra算法的带权有向图最短路径问题求解Python实现

Dijkstra算法简介

Dijkstra算法是一种贪心算法，它先求出长度最短的一条路径，再参照该最短路径求出长度次短的一条路径，直到求出从源点到其他各个顶点的最短路径。

具体的步骤

下面的介绍来自《趣学算法》

 

 

 

 

另一个例子用Python实现

用Python和Numpy实现寻找任意两点之间最小路径的算法，并用下图进行测试, 得到节点s和t之间的最短路径。 

对于上面这个图，Dijkstra算法的步骤如下：

1.先找到距离s点最近的点，即w

2.然后看与w相连接的点通过w再到那个点的距离近还是直接从s到这个点的距离近，由上图我们可以知道，与w相连的点是t和z，而t和z并不与s直接相连，因此更新最短距离数组和前驱数组

3.接着对距离s点第二近的点“X”重复第二个步骤，直到都执行完毕。（目的是看与“X”相连的点能否借助“X”获得更近的路径，即经过“X”，这就是上面的“借东风”）

下面的代码中，点s,v,u,w,z,t分别表示为点1,2,3,4,5,6

import numpy as np
import copy

def main():
    #无穷大
    infinity = float('inf')
    a = infinity
    #构建邻接矩阵
    adjacency_matrix = np.array([[a,6,5,3,a,a],
                                 [a,a,a,1,a,3],
                                 [a,a,a,1,2,a],
                                 [a,a,a,a,9,7],
                                 [a,a,a,a,a,5],
                                 [a,a,a,a,a,a]])
    #构建距离数组
    dist = np.array([0,6,5,3,a,a])
    #构建前驱数组
    precursor = np.array([-1,1,1,1,-1,-1])
    #初始集合
    S = {1}
    V = {1,2,3,4,5,6}
    V_subtract_S = V - S

    for i in range(len(V_subtract_S)-1):
        dist_copy = []
        V_subtract_S_list = list(V_subtract_S)
        for j in V_subtract_S:
            dist_copy.append(dist[j - 1])
        min_index = dist_copy.index(min(dist_copy))  # 查找dist_copy中最小的元素的位置
        S.add(V_subtract_S_list[min_index])
        current_node = V_subtract_S_list[min_index]
        V_subtract_S = V - S

        for j in V_subtract_S:
            dist_copy.append(dist[j - 1])
        for j in range(adjacency_matrix.shape[1]):
            if adjacency_matrix[current_node-1][j] < a:
                if dist[current_node-1] + adjacency_matrix[current_node-1][j] < dist[j]:
                    dist[j] = dist[current_node-1] + adjacency_matrix[current_node-1][j]
                    precursor[j] = current_node

    #打印最佳路径
    temp = 1
    path = []
    path.insert(0, 6)
    precursor = list(precursor)
    front_code = precursor[5]
    while temp:
        path.insert(0,front_code)
        #front_code的数字对应的另一个节点
        front_code_index = path[0] - 1
        front_code = precursor[front_code_index]
        if front_code == 1:
            temp = 0
    path.insert(0,1)
    for i in path:
        if i == 1:
            path[path.index(i)] = 's'
        if i == 2:
            path[path.index(i)] = 'v'
        if i == 3:
            path[path.index(i)] = 'u'
        if i == 4:
            path[path.index(i)] = 'w'
        if i == 5:
            path[path.index(i)] = 'z'
        if i == 6:
            path[path.index(i)] = 't'

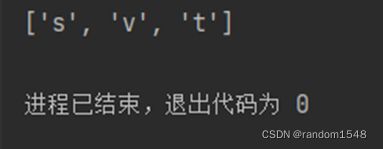
    print(path)

运行结果：