凸优化 机器学习 深度学习
This article provides a summary of popular optimizers used in computer vision, natural language processing, and machine learning in general. Additionally, you will find a guideline based on three questions to help you pick the right optimizer for your next machine learning project.
本文提供了用于计算机视觉,自然语言处理和一般机器学习的流行优化器的摘要。 此外,您将找到基于三个问题的指南,以帮助您为下一个机器学习项目选择合适的优化器。
TL;DR: 1) Find a related research paper and start with using the same optimizer. 2) Consult Table 1 and compare properties of your dataset to the strengths and weaknesses of the different optimizers. 3) Adapt your choice to the available resources.
TL; DR: 1)找到相关的研究论文,并从使用相同的优化器开始。 2)请参考表1 ,并将数据集的属性与不同优化器的优缺点进行比较。 3)使您的选择适应可用资源。
介绍 (Introduction)
Choosing a good optimizer for your machine learning project can be overwhelming. Popular deep learning libraries such as PyTorch or TensorFLow offer a broad selection of different optimizers — each with its own strengths and weaknesses. However, picking the wrong optimizer can have a substantial negative impact on the performance of your machine learning model [1][2]. This makes optimizers a critical design choice in the process of building, testing, and deploying your machine learning model.
为您的机器学习项目选择一个好的优化器可能会让人不知所措。 流行的深度学习库(例如PyTorch或TensorFLow)提供了多种不同的优化器选择-每个优化器都有其优点和缺点。 但是,选择错误的优化器可能会对您的机器学习模型的性能产生重大负面影响[1] [2]。 这使优化器成为构建,测试和部署机器学习模型过程中的关键设计选择。
The problem with choosing an optimizer is that, due to the no-free-lunch theorem, there is no single optimizer to rule them all; as a matter of fact, the performance of an optimizer is highly dependent on the setting. So, the central question that arises is:
选择优化器的问题在于,由于没有自由午餐定理,因此没有一个单独的优化器可以将所有规则都规则化。 实际上,优化器的性能高度取决于设置。 因此,出现的中心问题是:
Which optimizer suits the characteristics of my project the best?
哪种优化器最适合我项目的特点?
The following article is meant as a guide to answering the question above. It is structured into two main paragraphs: In the first part, I will present to you a quick introduction to the most frequently used optimizers. In the second part, I will provide you with a three-step plan to pick the best optimizer for your project.
以下文章旨在作为回答上述问题的指南。 它分为两个主要部分:在第一部分中,我将向您简要介绍最常用的优化器。 在第二部分中,我将为您提供一个三步计划,为您的项目选择最佳的优化器。
常用优化器 (Frequently Used Optimizers)
Almost all popular optimizers in deep learning are based on gradient descent. This means that they repeatedly estimate the slope of a given loss function L and move the parameters in the opposite direction (hence climbing down towards a supposed global minimum). The most simple example for such an optimizer is probably stochastic gradient descent (or SGD) which has been used since the 1950s [3]. In the 2010s the use of adaptive gradient methods such as AdaGrad or Adam [4][1] has become increasingly popular. However, recent trends show that parts of the research community move back towards using SGD over adaptive gradient methods, see for example [2] and [5]. Furthermore, current challenges in deep learning bring rise to new variants of SGD like LARS or LAMB [6][7]. For example, Google Research use LARS to train a powerful self-supervised model in one of their latest papers [8].
深度学习中几乎所有流行的优化器都基于梯度下降。 这意味着他们反复估算给定损失函数L的斜率,并沿相反方向移动参数(因此向下爬升至假定的全局最小值)。 这种优化器的最简单示例可能是自1950年代以来一直使用的随机梯度下降(SGD)[3]。 在2010年代,自适应梯度方法(例如AdaGrad或Adam [4] [1])的使用变得越来越流行。 但是,最近的趋势表明,研究界的某些部分转而使用自适应梯度法来使用SGD,例如参见[2]和[5]。 此外,当前的深度学习挑战带来了新的SGD变体,例如LARS或LAMB [6] [7]。 例如,Google Research在其最新论文之一中使用LARS训练了强大的自我监督模型[8]。
The section below will be an introduction to the most popular optimizers. Head to section How to Choose the Right Optimizer if you are already familiar with the concepts.
以下部分将介绍最流行的优化器。 如果您已经熟悉这些概念,请转至如何选择合适的优化器。
We will use the following notation: Denote by w the parameters and by g the gradients of the model. Furthermore, let α be the global learning rate of each optimizer and t the time step.
我们将使用以下符号:由w表示参数,由g表示模型的梯度。 此外,令α为每个优化器的整体学习率, t为时间步长。
Stochastic Gradient Descent (SGD) [9]
随机梯度下降(SGD)[9]
In SGD, the optimizer estimates the direction of steepest descent based on a mini-batch and takes a step in this direction. Because the step size is fixed, SGD can quickly get stuck on plateaus or in local minima.
在SGD中,优化器基于小批量估计最陡下降方向,并朝该方向迈出一步。 由于步长是固定的,因此SGD可能很快卡在高原或局部极小值上。
SGD with Momentum [10]:
SGD和动量[10]:
PyTorch, 20.07.2020). PyTorch ,20.07.2020)。Where β < 1. With momentum, SGD accelerates in directions of constant descent (that’s why it’s also called the “heavy ball method”). This acceleration helps the model escape plateaus and makes it less susceptible to getting stuck in local minima.
哪里 β<1。有了动量,SGD沿恒定下降的方向加速(这就是为什么它也被称为“重球法”)的原因。 这种加速有助于模型逃脱平稳状态,使其不易陷入局部极小值。
AdaGrad (2011, [4])
AdaGrad(2011,[4])
Update Rule for AdaGrad [4]. AdaGrad [4]的更新规则。AdaGrad is one of the first successful methods which makes use of adaptive learning rates (hence the name). AdaGrad scales the learning rate for each parameter based on the square root of the inverse of the sum of the squared gradients. This procedure scales sparse gradient directions up which in turn allows for larger steps in these directions. The consequence: AdaGrad can converge faster in scenarios with sparse features.
AdaGrad是利用自适应学习率(因此得名)的首批成功方法之一。 AdaGrad基于平方梯度之和的倒数的平方根来缩放每个参数的学习率。 此过程将稀疏渐变方向放大,这又允许在这些方向上进行较大的调整。 结果:在具有稀疏功能的场景中,AdaGrad可以更快地收敛。
RMSprop (2012, [11])
RMSprop(2012,[11])
Update Rule for RMSprop [11]. RMSprop [11]的更新规则。RMSprop is a non-published optimizer which has been used excessively in the last years. The idea is similar to AdaGrad but the rescaling of the gradient is less aggressive: The sum of squared gradients is replaced by a moving average of the squared gradients. RMSprop is often used with momentum and can be understood as an adaption of Rprop to the mini-batch setting.
RMSprop是未发布的优化器,最近几年已被过度使用。 这个想法与AdaGrad类似,但是渐变的重新缩放不太积极:用平方梯度的移动平均值代替平方梯度的总和。 RMSprop通常与动量一起使用,可以理解为Rprop对小批量设置的适应。
Adam (2014, [1])
亚当(2014,[1])
Update Rule for Adam [1]. 亚当[1]的更新规则。Adam combines AdaGrad, RMSprop and momentum methods into one. The direction of the step is determined by a moving average of the gradients and the step size is approximately upper bounded by the global step size . Furthermore, each dimension of the gradient is rescaled similar to RMSprop. One key difference between Adam and RMSprop (or AdaGrad) is the fact that the moment estimates m and v are corrected for their bias towards zero. Adam is well-known for achieving good performance with little hyper-parameter tuning.
亚当将AdaGrad,RMSprop和动量方法结合在一起。 阶跃的方向由梯度的移动平均值确定,阶跃大小大约由全局阶跃大小上限。 此外,类似于RMSprop,对梯度的每个维度进行重新缩放。 Adam和RMSprop(或AdaGrad)之间的一个主要区别是,对力矩估计m和v的零偏进行了校正。 Adam以很少的超参数调整就能获得良好的性能而闻名。
LARS (2017, [6])
LARS(2017,[6])
Update Rule for LARS [6]. LARS的更新规则[6]。LARS is an extension of SGD with momentum which adapts a learning rate per layer. It has recently caught attention in the research community. The reason is that due to the steadily growing amount of available data, distributed training of machine learning models has gained popularity. The consequence is that batch sizes begin growing. However, this leads to instabilities during training. Yang et al. [6] argue that these instabilities stem from an imbalance between the gradient norm and the weight norm for certain layers. They therefore came up with an optimizer which rescales the learning rate for each layer based on a “trust” parameter η < 1 and the inverse norm of the gradient for that layer.
LARS是SGD的扩展,具有动量,可以适应每层的学习率。 它最近在研究界引起了关注。 原因是由于可用数据量的稳定增长,机器学习模型的分布式训练已变得越来越流行。 结果是批次大小开始增长。 然而,这导致训练期间的不稳定。 杨等。 [6]认为,这些不稳定性源于某些层的梯度规范和权重规范之间的不平衡。 因此,他们提出了一个优化器,该优化器基于“信任”参数η<1和该层梯度的反范数来重新调整每个层的学习率。
如何选择合适的优化器? (How to Choose the Right Optimizer?)
As mentioned above, choosing the right optimizer for your machine learning problem can be hard. More specifically, there is no one-fits-all solution and the optimizer has to be carefully chosen based on the particular problem at hand. In the following section I will propose three questions you should ask yourself before deciding to use a certain optimizer.
如上所述,为您的机器学习问题选择合适的优化器可能很困难。 更具体地说,没有万能的解决方案,必须根据当前的特定问题仔细选择优化器。 在下一节中,我将提出三个问题,您在决定使用某个优化程序之前应该问自己。
What are the state-of-the-art results on datasets and tasks similar to yours? Which optimizers were used and why?
与您类似的数据集和任务的最新结果是什么? 使用了哪些优化器,为什么?
If you are working with novel machine learning methods, odds are there exist one or more reliable papers which cover a similar problem or handle similar data. Oftentimes the authors of the paper have done extensive cross-validation and report only the most successful configurations. Try to understand the reasoning for their choice of optimizer.
如果您正在使用新颖的机器学习方法,那么可能存在一篇或多篇可靠的论文,这些论文涵盖了类似的问题或处理了类似的数据。 通常,本文的作者已经进行了广泛的交叉验证,并且仅报告了最成功的配置。 尝试了解选择优化器的原因。
Example: Say you want to train a Generative Adversarial Network (GAN) to perform super-resolution on a set of images. After some research you stumble upon this [12] paper in which the researchers used the Adam optimizer to solve the exact same problem. Wilson et al. [2] argue that training GANs does not correspond to solving optimization problems and that Adam may be well-suited for such scenarios. Hence, in this case, Adam is a good choice for an optimizer.
示例:假设您要训练生成对抗网络(GAN),以对一组图像执行超分辨率。 经过一番研究后,您偶然发现了这份[12]论文,研究人员使用Adam优化器解决了完全相同的问题。 威尔逊等。 [2]认为训练GAN并不对应于解决优化问题,并且Adam可能非常适合这种情况。 因此,在这种情况下,亚当是优化程序的不错选择。
Are there characteristics to your dataset which play to the strengths of certain optimizers? If so, which ones and how?
您的数据集中是否存在可以发挥某些优化器优势的特征? 如果是这样,哪个以及如何?
Table 1 shows an overview of the different optimizers with their strengths and weaknesses. Try to find an optimizer which matches the characteristics of your dataset, training setup, and goal of the project.
表1概述了不同优化器的优缺点。 尝试找到与数据集的特征,训练设置和项目目标相匹配的优化器。
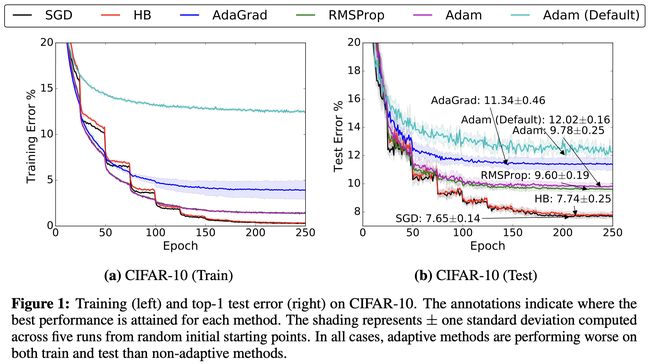
Certain optimizers perform extraordinarily well on data with sparse features [13] and others may perform better when the model is applied to previously unseen data [14]. Some optimizers work very well with large batch sizes [6] while others will converge to sharp minima with poor generalization [15].
某些优化器在具有稀疏特征的数据上表现出色[13],而其他一些将模型应用于先前未见过的数据时可能会表现更好[14]。 一些优化器在大批处理量下可以很好地工作[6],而另一些优化器会在泛化不佳的情况下收敛到极小的最小值[15]。
Example: For a project at your current job you have to classify written user responses into positive and negative feedback. You consider to use bag-of-words as input features for your machine learning model. Since these features can be very sparse you decide to go for an adaptive gradient method. But which one do you want to use? Consulting Table 1, you see that AdaGrad has the fewest tunable parameters of the adaptive gradient methods. Seeing the limited time frame of your project you choose AdaGrad as an optimizer.
示例:对于当前工作的项目,您必须将书面用户反馈分为正面和负面反馈。 您考虑使用词袋作为机器学习模型的输入功能。 由于这些功能可能非常稀疏,因此您决定采用自适应梯度方法。 但是,您要使用哪一个? 咨询表1 ,您会发现AdaGrad的自适应梯度方法的可调参数最少。 鉴于项目的时间有限,您选择了AdaGrad作为优化器。
What are your resources for the project?
您对该项目有哪些资源?
The resources which are available for a project also have an effect on which optimizer to pick. Computational limits or memory constraints, as well as the time frame of the project can narrow down the set of feasible choices. Looking again at Table 1, you can see the different memory requirements and number of tunable parameters for each optimizer. This information can help you estimate whether or not the required resources of an optimizer can be supported by your setup.
可用于项目的资源也会影响选择哪个优化程序。 计算限制或内存限制以及项目的时间范围可以缩小可行选择的范围。 再次查看表1 ,您可以看到每个优化器的不同内存需求和可调参数的数量。 此信息可以帮助您估计设置是否可以支持优化器的所需资源。
Example: You are working on a project in your free-time in which you want to train a self-supervised model (e.g. SimCLR [16]) on an image dataset on your home computer. For models like SimCLR, the performance increases with an increased batch size. Therefore, you want to save as much memory as possible so that you can do training in large batches. You choose a simple stochastic gradient descent without momentum as your optimizer because, in comparison to the other optimizers, it requires the least amount of additional memory to store the state.
示例:您正在业余时间从事一个项目,该项目中您想在家用计算机上的图像数据集上训练一个自我监督模型(例如SimCLR [16])。 对于SimCLR之类的模型,性能随着批处理大小的增加而提高。 因此,您想要节省尽可能多的内存,以便可以进行大批量的培训。 您选择没有动量的简单随机梯度下降作为优化器,因为与其他优化器相比,它需要最少的额外内存来存储状态。
Conclusion
结论
Trying out all possible optimizers to find the best one for a project is not always possible. In this blog post I provided an overview over the update rules, strengths, weaknesses, and requirements of the most popular optimizers. Furthermore, I listed three questions to guide you towards making an informed decision about which optimizer to use for your machine learning project.
并非总是可能尝试所有可能的优化器来为项目找到最佳的优化器。 在这篇博客中,我概述了最流行的优化器的更新规则,优点,缺点和要求。 此外,我列出了三个问题,以指导您做出明智的决定,以决定将哪种优化器用于您的机器学习项目。
As a rule of thumb: If you have the resources to find a good learning rate schedule, SGD with momentum is a solid choice. If you are in need of quick results without extensive hypertuning, tend towards adaptive gradient methods.
根据经验:如果您有足够的资源找到良好的学习进度表,那么具有动力的SGD是一个不错的选择。 如果您需要快速的结果而不需要大量的超调,则倾向于使用自适应梯度方法。
I hope that this blog post will serve as a helpful orientation and that I could assist one or the other in making the right optimizer choice.
我希望这篇博客文章能对您有所帮助,并希望我能帮助一个或另一个人做出正确的优化器选择。
I am open for feedback, let me know if you have any suggestions in the comments!
我愿意征求反馈,如果您有任何建议,请告诉我!
Philipp WirthMachine Learning EngineerWhatToLabel.com
Philipp Wirth机器学习工程师WhatToLabel.com
[1]: Kingma, D. P. & Ba, J. (2014), ‘Adam: A Method for Stochastic Optimization’ , cite arxiv:1412.6980Comment: Published as a conference paper at the 3rd International Conference for Learning Representations, San Diego, 2015 .
[1]:Kingma,DP和Ba,J.(2014),“亚当:一种随机优化方法”,引用arxiv:1412.6980评论:作为会议论文在第三届国际学习代表大会上发表,圣地亚哥,2015年。
[2]: Wilson, Ashia C. et al. “The Marginal Value of Adaptive Gradient Methods in Machine Learning.” ArXiv abs/1705.08292 (2017): n. pag.
[2]:Wilson,Ashia C.等。 “自适应梯度方法在机器学习中的边际价值。” ArXiv abs / 1705.08292(2017):n。 帕格
[3]: Robbins, Herbert; Monro, Sutton. A Stochastic Approximation Method. Ann. Math. Statist. 22 (1951), no. 3, 400–407. doi:10.1214/aoms/1177729586. https://projecteuclid.org/euclid.aoms/1177729586
[3]:罗宾斯,赫伯特; 萨罗·梦露随机近似法。 安数学。 统计员。 22(1951),没有。 3,400-407。 doi:10.1214 / aoms / 1177729586。 https://projecteuclid.org/euclid.aoms/1177729586
[4]: Duchi, J. C.; Hazan, E. & Singer, Y. (2011), ‘Adaptive Subgradient Methods for Online Learning and Stochastic Optimization.’, J. Mach. Learn. Res. 12 , 2121–2159.
[4]:Duchi,JC; Hazan,E.&Singer,Y.(2011),“在线学习和随机优化的自适应次梯度方法”,J。Mach 。 学习。 Res。 12,2121年至2159年。
[5]: Keskar, Nitish Shirish and Richard Socher. “Improving Generalization Performance by Switching from Adam to SGD.” ArXiv abs/1712.07628 (2017): n. pag.
[5]:Keskar,Nitish Shirish和Richard Socher。 “通过从Adam切换到SGD来提高通用性能。” ArXiv abs / 1712.07628(2017):n。 帕格
[6]: You, Yang et al. (2017) ‘Large Batch Training of Convolutional Networks.’ arXiv: Computer Vision and Pattern Recognition (2017): n. pag.
[6]:您,Yang等。 (2017)'卷积网络的大批量训练'。 arXiv:计算机视觉和模式识别(2017):n。 帕格
[7]: You, Yang et al. “Large Batch Optimization for Deep Learning: Training BERT in 76 minutes.” arXiv: Learning (2020): n. pag.
[7]:您,Yang等。 “用于深度学习的大批量优化:在76分钟内训练BERT。” arXiv:学习(2020):n。 帕格
[8]: Grill, Jean-Bastien et al. “Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning.” ArXiv abs/2006.07733 (2020): n. pag.
[8]:Grill,Jean-Bastien等。 “引导自己的潜能:一种自我指导学习的新方法。” ArXiv abs / 2006.07733(2020):n。 帕格
[9]: Bharath, B., Borkar, V.S. Stochastic approximation algorithms: Overview and recent trends. Sadhana 24, 425–452 (1999). https://doi.org/10.1007/BF02823149
[9]:Bharath,B.,Borkar,VS随机近似算法:概述和最新趋势。 修习24,425-452(1999)。 https://doi.org/10.1007/BF02823149
[10]: David E. Rumelhart, Geoffrey E. Hinton, and Ronald J. Williams. 1988. Learning representations by back-propagating errors. Neurocomputing: foundations of research. MIT Press, Cambridge, MA, USA, 696–699.
[10]:David E. Rumelhart,Geoffrey E. Hinton和Ronald J. Williams。 1988年。通过向后传播的错误学习表示形式。 神经计算:研究的基础。 麻省理工学院出版社,美国马萨诸塞州剑桥,696–699。
[11]: Tieleman, T. and Hinton, G., 2012. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural networks for machine learning, 4(2), pp.26–31.
[11]:Tieleman,T。和Hinton,G.,2012年。第6.5讲:均方根:将梯度除以最近幅度的移动平均值。 COURSERA:用于机器学习的神经网络, 4 (2),第26–31页。
[12]: C. Ledig et al., “Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network,” 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, 2017, pp. 105–114, doi: 10.1109/CVPR.2017.19.
[12]:C. Ledig等人,“使用生成的对抗网络实现逼真的单图像超分辨率”, 2017 IEEE计算机视觉和模式识别会议(CVPR) ,檀香山,HI,2017年,第105–105页114,doi:10.1109 / CVPR.2017.19。
[13]: John Duchi, Elad Hazan, and Yoram Singer. 2011. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 12, null (2/1/2011), 2121–2159.
[13]: John Duchi,Elad Hazan和Yoram Singer。 2011。在线学习和随机优化的自适应次梯度方法。 J.马赫学习。 Res。 12,空(2/1/2011),2121–2159。
[14]: Moritz Hardt, Benjamin Recht, and Yoram Singer. 2016. Train faster, generalize better: stability of stochastic gradient descent. In Proceedings of the 33rd International Conference on International Conference on Machine Learning — Volume 48(ICML’16). JMLR.org, 1225–1234.
[14]:莫里兹·哈特,本杰明·雷特和约拉姆·辛格。 2016年。训练更快,推广效果更好:随机梯度下降的稳定性。 在第33届国际机器学习国际会议国际会议录中,第48卷(ICML'16)。 JMLR.org,1225-1234。
[15]: Keskar, Nitish Shirish et al. “On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima.” ArXiv abs/1609.04836 (2017): n. pag.
[15]:Keskar,Nitish Shirish等。 “关于深度学习的大批量培训:泛化差距和夏普最小值”。 ArXiv abs / 1609.04836(2017):n。 帕格
[16]: Chen, Ting et al. “A Simple Framework for Contrastive Learning of Visual Representations.” ArXiv abs/2002.05709 (2020): n. pag.
[16]:陈婷等。 “视觉表示形式对比学习的简单框架。” ArXiv abs / 2002.05709(2020):n。 帕格
翻译自: https://towardsdatascience.com/which-optimizer-should-i-use-in-my-machine-learning-project-5f694c5fc280
凸优化 机器学习 深度学习