- 【仿muduo库实现并发服务器】Connection模块
tew_gogogo
项目服务器网络android
仿muduo库实现并发服务器一.Connection模块二.成员变量1.连接唯一ID(连接管理)2.Socket对象(套接字操作管理)3.Channel对象(连接事件管理)4.Buffer对象(缓冲区管理)5.ConnStatus对象(连接状态管理)6.EventLoop对象(连接监控/定时任务管理)7.Any对象(上下文管理)8.是否启动非活跃超时连接销毁标志位9.5个阶段性回调函数三.成员函数
- Python Scrapy的爬虫中间件开发
AI天才研究院
pythonscrapy爬虫ai
PythonScrapy爬虫中间件开发:从原理到实战的深度解析关键词Scrapy中间件、爬虫扩展、请求响应处理、反爬绕过、中间件生命周期、钩子函数、分布式爬取摘要本文系统解析Scrapy爬虫中间件(SpiderMiddleware)的开发方法论,覆盖从基础概念到高级实践的全链路知识。通过第一性原理推导中间件的核心机制,结合层次化架构分析(理论→设计→实现→应用),提供生产级代码示例与可视化流程模型
- 【仿muduo库实现并发服务器】LoopThreadPool模块
仿muduo库实现并发服务器1.LoopThread模块1.1成员变量1.2构造函数13线程入口函数1.4获取eventloop对象GetLoop()2.LoopThreadPool模块2.1成员变量2.2构造函数2.3配置线程数量2.4按照配置数量创建线程2.5依次分配Eventloop对象1.LoopThread模块这个模块是为了将EventLoop与线程整合起来。一个EventLoop对应一
- 【Vue.js】 Mixin 局部混入与全局混入的介绍和使用总结以及优缺点分析
生活、追梦者
vuevue.js前端javascript
1.Vue.jsMixin概述1.1Mixin的定义与作用Mixin在Vue.js中是一种灵活的组件复用机制。它允许我们将多个组件之间的共通功能抽象出来,形成一个混入对象。这样,我们就可以避免在多个组件中重复编写相同的代码,提高代码的复用性和可维护性。Mixin对象可以包含多种组件选项,如数据(data)、计算属性(computed)、方法(methods)、生命周期钩子(lifecyclehoo
- 前端常见面试题
黄马小配件
前端csshtml
sass语言的特点?1.可以减少重复代码:Sass可以通过使用变量、混合、继承等方式来减少代码的重复性,提高代码的可维护性。2.支持嵌套:Sass支持CSS样式的嵌套,可以更方便地控制样式的层级关系。3.支持模块化:Sass支持模块化开发,可以将样式分成多个模块进行开发,提高代码的可读性和可维护性。4.支持函数和运算符:Sass支持函数和运算符,可以完成更复杂的样式计算。5.支持导入其他文件:Sa
- (纯新手练习五)python基础代码,我手把手带你敲(类与对象,实例,构造函数__init__初始化对象属性,继承,方法重写,类的文档字符串,模块化)
星期天要睡觉
python开发语言
目录1.基本理论简述类与对象构造函数(Constructor)继承(Inheritance)方法重写(MethodOverriding)四者关系总结类的文档字符串(Docstring)2.练习开始3.代码模块化练习(纯新手练习五)python基础代码,我手把手带你敲(类与对象,实例,构造函数__init__初始化对象属性,继承,方法重写,类的文档字符串,模块化)(下一节课:文件操作)基本理论简述类
- (C++)学生管理系统(正式版)(map数组的应用)(string应用)(引用)(文件储存的应用)(C++教学)(C++项目)
目录源代码:代码详解:学生成绩管理系统实现详解一、系统整体设计思路1.数据结构选择2.功能模块划分二、关键函数实现原理1.文件存储与加载save_file函数load_file函数2.核心数据操作add函数mod函数find和del函数3.数据展示display函数statistics函数三、核心技术详解1.字符串分割技术2.map的使用技巧3.文件格式设计4.错误处理机制源代码:/**头文件部分
- 【基础】C++中的关键词
小熊猫爱编程
重新学编程c++开发语言
一、关键词的概念C++中的关键词是语言保留用来表示特定语法结构的单词,不能作为变量名、函数名或标识符使用。二、关键词有哪些在C++中有63个关键字,如下:关键词关键词关键词关键词关键词asmdoifreturntypedefautodoubleinlineshorttypeidbooldynamic_castintsignedtypenamebreakelselongsizeofunioncase
- NestJS 系列教程(一):认识 NestJS 与项目初始化
onebyte8bits
nestjs后端javascript前端框架node.js
NestJS系列教程(一):认识NestJS与项目初始化✨前言NestJS是一个用于构建高效、可扩展Node.js服务端应用程序的框架。它使用TypeScript构建,结合了面向对象编程(OOP)、函数式编程(FP)和函数响应式编程(FRP)等概念,非常适合用于构建微服务、RESTfulAPI等现代服务端应用。本系列教程将以NestJS官方中文文档为蓝本,逐章精讲配套代码,带你系统学习这一现代No
- 嵌入式入门学习——5了解寄存器如何控制单片机
星火嵌入式
嵌入式入门学习单片机
0系列文章入口嵌入式入门学习——0快速入门,Let‘sDoIt!1.内容简介武侠的内功和招式之间的关系类似于编程中的技术和计算原理之间的关系。招式是千变万化的,而内功心法则稳定而深厚。内功心法的深度决定了可以学习的招式变术的上限高度。单片机的控制最终是要落实到寄存器上的。使用库函数或者使用高级语言是招式,了解单片机的寄存器则是内功。2.引言练习武功讲究内外兼修,一味学习技巧,而忽略本质的结果就是一
- 你以为的 () 只是函数调用?栈的战争:函数调用背后,编译器、链接器、CPU与黑客的四方博弈 解剖CPU、内存与安全交织的底层真相 了解函数调用的暗流:从C括号到CPU指令、栈帧攻防的生死时速
small_wh1te_coder
c++c算法c语言c++c算法面试
作者:smallcodewhite更新:2025.6.4号下午6点13分小引子:在软件这行当里混久了,你会发现一个现象:很多人能用各种高级语言、框架写出复杂的业务,但一遇到诡异的崩溃、性能瓶颈,或者需要和底层硬件打交道时,就抓瞎了。究其原因,是对计算机体系最基础的运行模型理解得不够透。上一篇我们聊了点数据在内存里的存放问题,有兄弟说不够劲,没触及灵魂。说得好。今天,咱们就来干一件有挑战性的事:把C
- 【深度学习】神经网络剪枝方法的分类
烟锁池塘柳0
机器学习与深度学习深度学习神经网络剪枝
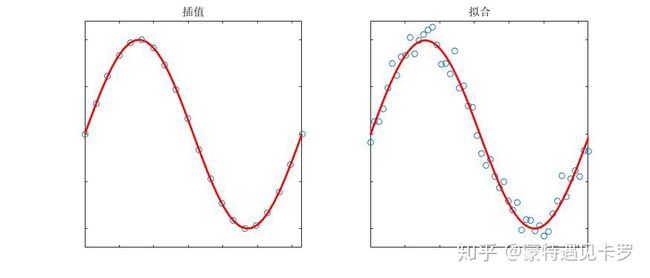
神经网络剪枝方法的分类摘要随着深度学习模型,特别是大语言模型(LLM)的参数量爆炸式增长,模型的部署和推理成本变得异常高昂。如何在保持模型性能的同时,降低其计算和存储需求,成为了工业界和学术界的核心议题。神经网络剪枝(Pruning)作为模型压缩的关键技术之一,应运而生。本文将解析剪枝技术的不同分类,深入探讨其原理、优缺点。文章目录神经网络剪枝方法的分类摘要1为什么我们需要剪枝?2分类方法一:剪什
- 基于条件风险价值CVaR的微网动态定价与调度策略(Matlab代码实现)
Ps.729
matlab开发语言
个人主页欢迎来到本博客❤️❤️博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。⛳️座右铭:行百里者,半于九十。本文目录如下:目录1概述一、CVaR的理论基础及其在微网中的适用性1.CVaR的定义与优势2.微网应用场景适配性二、动态定价与调度模型的联合优化框架1.目标函数设计2.动态定价机制3.不确定性处理方法三、关键算法与求解策略1.随机规划与CVaR集成2.智能优化算法对比四、实证
- 机器视觉通用平台之拟合圆工具类
小治视觉
算法visualstudioc#
usingSystem;usingSystem.Collections.Generic;usingSystem.Linq;usingSystem.Runtime.InteropServices;usingSystem.Text;usingSystem.Threading.Tasks;usingCvBase;usingSystem.IO;usingSystem.Drawing.Drawing2D;u
- R 语言安装使用教程
小奇JAVA面试
安装使用教程r语言开发语言
一、R语言简介R是一种用于统计分析、数据挖掘和可视化的编程语言和环境。它在学术界和数据分析领域中广泛使用,拥有丰富的统计函数库和绘图功能。二、安装R语言2.1下载R安装包前往CRAN官网下载适合你操作系统的安装程序:官网地址:https://cran.r-project.org/2.2Windows安装下载.exe安装包;双击安装程序,按默认选项一路安装即可;安装完成后,可通过RGUI或命令行启动
- VB.NET版本小钢琴程序代码2024-8-2-QZQ
EYYLTV
.net
ImportsSystem.Runtime.InteropServicesImportsSystem.ThreadingPublicClassForm1'义WindowsAPI函数PrivateSharedFunctionmidiOutGetNumDevs()AsIntegerEndFunctionPrivateSharedFunctionmidiOutGetDevCaps(ByValuDevic
- 深度学习相关指标工作笔记
Victor Zhong
AI框架深度学习笔记人工智能
这里写目录标题检测指标iou/Gou/Diou/CiouMSE(MeanSquaredError)(均方误差)(回归问题)交叉熵损失函数(CrossEntropyErrorFunction)(分类问题)检测指标iou/Gou/Diou/CiouIntersectionoverUnion(IoU)是目标检测里一种重要的评价值交并比令人遗憾的是IoU无法优化无重叠的bboxes如果用IoU作为loss
- 前端手写题(二)
目录一、new二、call三、apply四、bind五、create一、newnew的核心作用:基于构造函数创建实例,绑定原型链,初始化对象属性。底层四步:创建空对象→绑定原型→执行构造函数→处理返回值functionobjectFactory(constructor,...args){ //严格校验构造函数 if(typeofconstructor!=='function'){ throwne
- The 2022 ICPC Asia Xian Regional Contest(E,L)题解
啊这.-
算法c++数据结构
EFindMaximum题意:首先,通过观察与打表,可以发现:规律:对于非负整数x,函数f(x)的值等于:将xx写成三进制后,各个位数的数字之和+该三进制数的位数。例如,x=1002(3),则有f(1002(3))=(1+0+0+2)+4=7。最大化策略:由于f(x)的值为「位数之和+位数」,为了尽可能让f(x)最大,我们需要:尽可能多地让每个位为数字2,因为2是三进制单个位的最大贡献。因此问题转
- Solidity 合约引入、调用、继承与重写详解
yoona1020
区块链Solidity继承重写
目录引言一、引入其他合约二、调用已部署合约三、代码讲解四、继承与重写(override)(一)基础继承与重写(二)多重继承与override(Base1,Base2)(三)super调用多层父方法(四)重写可见性与函数签名五、构造函数继承总结引言在Solidity开发中,模块化设计是构建高效、可维护智能合约的关键。通过引入其他合约、调用已部署合约以及合理使用继承与方法重写,开发者可以实现代码复用、
- Open3D 点到面的ICP配准算法
AtlasCloud
python点云数据处理算法人工智能python矩阵numpy
目录一、算法原理1、算法概述2、点到平面ICP精配准3、参考文献二、主要函数三、代码实现四、结果展示1、初始位置2、配准结果一、算法原理1、算法概述 点到平面度量通常使用标准非线性最小二乘法来求解,例如Levenberg-Marquardt。点到平面ICP算法的每次迭代通常比点到点算法慢,但收敛速度明显更快。两个点云之间的相对旋转小于30°,在旋转矩阵中用θ替换sinθ,用1替换cosθ实现用线
- C++基础复习笔记
xuwzen
C++c++笔记
一、数组定义在C++中,数组初始化有多种方式,以下是常见的几种方法:默认初始化数组元素未显式初始化时,内置类型(如int、float)的元素值未定义(垃圾值),类类型调用默认构造函数。intarr1[5];//元素值未定义聚合初始化(列表初始化)使用花括号{}直接初始化所有元素。若列表元素少于数组长度,剩余元素默认初始化(内置类型为0)。intarr2[3]={1,2,3};//完全初始化inta
- LK32T102学习-0
和风化雨
嵌入式系统LK32T单片机嵌入式硬件
工程建立步骤:建立一个文件夹,文件夹的名称就是任务名称,如XX将test1-gpio文件夹中的内容全部拷贝到XX通过uVision(或直接点击XX文件夹下的*.uvprojx)打开工程打开工程文件夹下的main.c文件修改main函数,其余不动main函数结构intmain(){ Device_Init();//不要动 //添加你的其他初始化代码 while(1){//工作循环//添加
- STM32开发方式及基本介绍
相关推荐STM32新建一个工程STM32的开发有三种方式1.寄存器版本2.库函数版本3.HAL库版本一、库函数开发与寄存器开发的关系很多人都是从学51单片机转而想进一步学习STM32,他们习惯了51单片机的寄存器开发方式,ST官方库摆在面前会不知道从何下手。其实简单来说,固件库就是函数的集合,固件库函数的作用是向下负责与寄存器直接打交道,向上提供用户函数调用的接口。举一个例子来解释STM32固件库
- JWT鉴权的流程和原理
hwg985
八股-java基础Java鉴权JWT
文章目录1\.JWT的原理:它是什么构成的?a)第一部分:Header(头部)b)第二部分:Payload(载荷)c)第三部分:Signature(签名)2\.JWT的鉴权流程3\.JWT的优缺点优点:缺点:好的,我们来详细、清晰地介绍一下JWT(JSONWebToken)的鉴权流程和其背后的原理。这是一个在现代Web应用和API安全中非常核心的概念。我将用一个通俗的比喻来帮助你理解:传统的Ses
- 八、测试与调试
目录1.Flutter测试的类型有哪些?2.如何编写单元测试?3.如何测试Widget?4.什么是Golden测试?5.如何使用FlutterDevTools?1.Flutter测试的类型有哪些?Flutter测试主要分为三类,覆盖不同粒度的质量保障:测试类型测试对象执行速度依赖环境主要工具单元测试独立函数/类极快(1s)模拟器/真机integration_test包特殊测试类型:Golden测试
- SQLiteC/C++接口详细介绍sqlite3_stmt类(一)
界忆
数据库SQLiteC与c++sqlite数据库
返回目录:SQLite—免费开源数据库系列文章目录上一篇:SQLiteC/C++接口详细介绍sqlite3_stmt类简介下一篇:SQLiteC/C++接口详细介绍sqlite3_stmt类(二)序言:本文开始了SQLite的第二个类的详细介绍了,有兴趣的朋友可以关注更新一下。1、sqlite3_prepare_v2()`sqlite3_prepare_v2`是SQLite库中的一个函数,用于将一
- R语言开发记录,一
[email protected]
R语言r语言开发语言
1.清理环境rm(list=ls())gc()rm(list=ls())作用:删除当前R工作环境中所有的对象(变量、函数、数据框等)。解释:ls():列出当前环境中所有对象的名字。list=ls():将这些名字作为一个列表传给rm()函数。rm():移除这些对象。效果:相当于“清空内存”,让工作空间恢复到干净状态。gc()作用:手动触发垃圾回收(garbagecollection)。效果:释放R不
- 嵌入式Linux-线程同步-自旋锁和读写锁
线程同步一、自旋锁1.1自旋锁概述1.2自旋锁的初始化1.3自旋锁加锁和解锁二、读写锁2.1何为读写锁2.2读写函数初始化2.3读写锁上锁和解锁2.4读写锁的属性一、自旋锁1.1自旋锁概述自旋锁与互斥锁很相似,从本质上说也是一把锁,在访问共享资源之前对自旋锁进行上锁,在访问完成后释放自旋锁(解锁);事实上,从实现方式上来说,互斥锁是基于自旋锁来实现的,所以自旋锁相较于互斥锁更加底层。如果在获取自旋
- 『 Linux 』线程安全的单例模式,自旋锁与读写锁
Dio夹心小面包
线程LinuxC++linux单例模式javascript服务器c++运维
文章目录单例模式懒汉模式与饿汉模式自旋锁读写锁单例模式单例模式是一种创建型设计模式,其主要目的是确保一个类只有一个实例,并提供一个全局访问点来访问该实例;这在需要严格控制如何及合适访问某个唯一资源型下有一定作用;单利模式的主要特点为如下:私有构造函数单例模式通常要将构造私有化,以保证无法直接通过该类实例化出对应的对象;只能通过该类提供对应的接口来实例化整个对象,确保只有一个实例;私有静态实例私有静
- Spring4.1新特性——综述
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- Schema与数据类型优化
annan211
数据结构mysql
目前商城的数据库设计真是一塌糊涂,表堆叠让人不忍直视,无脑的架构师,说了也不听。
在数据库设计之初,就应该仔细揣摩可能会有哪些查询,有没有更复杂的查询,而不是仅仅突出
很表面的业务需求,这样做会让你的数据库性能成倍提高,当然,丑陋的架构师是不会这样去考虑问题的。
选择优化的数据类型
1 更小的通常更好
更小的数据类型通常更快,因为他们占用更少的磁盘、内存和cpu缓存,
- 第一节 HTML概要学习
chenke
htmlWebcss
第一节 HTML概要学习
1. 什么是HTML
HTML是英文Hyper Text Mark-up Language(超文本标记语言)的缩写,它规定了自己的语法规则,用来表示比“文本”更丰富的意义,比如图片,表格,链接等。浏览器(IE,FireFox等)软件知道HTML语言的语法,可以用来查看HTML文档。目前互联网上的绝大部分网页都是使用HTML编写的。
打开记事本 输入一下内
- MyEclipse里部分习惯的更改
Array_06
eclipse
继续补充中----------------------
1.更改自己合适快捷键windows-->prefences-->java-->editor-->Content Assist-->
Activation triggers for java的右侧“.”就可以改变常用的快捷键
选中 Text
- 近一个月的面试总结
cugfy
面试
本文是在学习中的总结,欢迎转载但请注明出处:http://blog.csdn.net/pistolove/article/details/46753275
前言
打算换个工作,近一个月面试了不少的公司,下面将一些面试经验和思考分享给大家。另外校招也快要开始了,为在校的学生提供一些经验供参考,希望都能找到满意的工作。
- HTML5一个小迷宫游戏
357029540
html5
通过《HTML5游戏开发》摘抄了一个小迷宫游戏,感觉还不错,可以画画,写字,把摘抄的代码放上来分享下,喜欢的同学可以拿来玩玩!
<html>
<head>
<title>创建运行迷宫</title>
<script type="text/javascript"
- 10步教你上传githib数据
张亚雄
git
官方的教学还有其他博客里教的都是给懂的人说得,对已我们这样对我大菜鸟只能这么来锻炼,下面先不玩什么深奥的,先暂时用着10步干净利索。等玩顺溜了再用其他的方法。
操作过程(查看本目录下有哪些文件NO.1)ls
(跳转到子目录NO.2)cd+空格+目录
(继续NO.3)ls
(匹配到子目录NO.4)cd+ 目录首写字母+tab键+(首写字母“直到你所用文件根就不再按TAB键了”)
(查看文件
- MongoDB常用操作命令大全
adminjun
mongodb操作命令
成功启动MongoDB后,再打开一个命令行窗口输入mongo,就可以进行数据库的一些操作。输入help可以看到基本操作命令,只是MongoDB没有创建数据库的命令,但有类似的命令 如:如果你想创建一个“myTest”的数据库,先运行use myTest命令,之后就做一些操作(如:db.createCollection('user')),这样就可以创建一个名叫“myTest”的数据库。
一
- bat调用jar包并传入多个参数
aijuans
下面的主程序是通过eclipse写的:
1.在Main函数接收bat文件传递的参数(String[] args)
如: String ip =args[0]; String user=args[1]; &nbs
- Java中对类的主动引用和被动引用
ayaoxinchao
java主动引用对类的引用被动引用类初始化
在Java代码中,有些类看上去初始化了,但其实没有。例如定义一定长度某一类型的数组,看上去数组中所有的元素已经被初始化,实际上一个都没有。对于类的初始化,虚拟机规范严格规定了只有对该类进行主动引用时,才会触发。而除此之外的所有引用方式称之为对类的被动引用,不会触发类的初始化。虚拟机规范严格地规定了有且仅有四种情况是对类的主动引用,即必须立即对类进行初始化。四种情况如下:1.遇到ne
- 导出数据库 提示 outfile disabled
BigBird2012
mysql
在windows控制台下,登陆mysql,备份数据库:
mysql>mysqldump -u root -p test test > D:\test.sql
使用命令 mysqldump 格式如下: mysqldump -u root -p *** DBNAME > E:\\test.sql。
注意:执行该命令的时候不要进入mysql的控制台再使用,这样会报
- Javascript 中的 && 和 ||
bijian1013
JavaScript&&||
准备两个对象用于下面的讨论
var alice = {
name: "alice",
toString: function () {
return this.name;
}
}
var smith = {
name: "smith",
- [Zookeeper学习笔记之四]Zookeeper Client Library会话重建
bit1129
zookeeper
为了说明问题,先来看个简单的示例代码:
package com.tom.zookeeper.book;
import com.tom.Host;
import org.apache.zookeeper.WatchedEvent;
import org.apache.zookeeper.ZooKeeper;
import org.apache.zookeeper.Wat
- 【Scala十一】Scala核心五:case模式匹配
bit1129
scala
package spark.examples.scala.grammars.caseclasses
object CaseClass_Test00 {
def simpleMatch(arg: Any) = arg match {
case v: Int => "This is an Int"
case v: (Int, String)
- 运维的一些面试题
yuxianhua
linux
1、Linux挂载Winodws共享文件夹
mount -t cifs //1.1.1.254/ok /var/tmp/share/ -o username=administrator,password=yourpass
或
mount -t cifs -o username=xxx,password=xxxx //1.1.1.1/a /win
- Java lang包-Boolean
BrokenDreams
boolean
Boolean类是Java中基本类型boolean的包装类。这个类比较简单,直接看源代码吧。
public final class Boolean implements java.io.Serializable,
- 读《研磨设计模式》-代码笔记-命令模式-Command
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.Collection;
import java.util.List;
/**
* GOF 在《设计模式》一书中阐述命令模式的意图:“将一个请求封装
- matlab下GPU编程笔记
cherishLC
matlab
不多说,直接上代码
gpuDevice % 查看系统中的gpu,,其中的DeviceSupported会给出matlab支持的GPU个数。
g=gpuDevice(1); %会清空 GPU 1中的所有数据,,将GPU1 设为当前GPU
reset(g) %也可以清空GPU中数据。
a=1;
a=gpuArray(a); %将a从CPU移到GPU中
onGP
- SVN安装过程
crabdave
SVN
SVN安装过程
subversion-1.6.12
./configure --prefix=/usr/local/subversion --with-apxs=/usr/local/apache2/bin/apxs --with-apr=/usr/local/apr --with-apr-util=/usr/local/apr --with-openssl=/
- sql 行列转换
daizj
sql行列转换行转列列转行
行转列的思想是通过case when 来实现
列转行的思想是通过union all 来实现
下面具体例子:
假设有张学生成绩表(tb)如下:
Name Subject Result
张三 语文 74
张三 数学 83
张三 物理 93
李四 语文 74
李四 数学 84
李四 物理 94
*/
/*
想变成
姓名 &
- MySQL--主从配置
dcj3sjt126com
mysql
linux下的mysql主从配置: 说明:由于MySQL不同版本之间的(二进制日志)binlog格式可能会不一样,因此最好的搭配组合是Master的MySQL版本和Slave的版本相同或者更低, Master的版本肯定不能高于Slave版本。(版本向下兼容)
mysql1 : 192.168.100.1 //master mysq
- 关于yii 数据库添加新字段之后model类的修改
dcj3sjt126com
Model
rules:
array('新字段','safe','on'=>'search')
1、array('新字段', 'safe')//这个如果是要用户输入的话,要加一下,
2、array('新字段', 'numerical'),//如果是数字的话
3、array('新字段', 'length', 'max'=>100),//如果是文本
1、2、3适当的最少要加一条,新字段才会被
- sublime text3 中文乱码解决
dyy_gusi
Sublime Text
sublime text3中文乱码解决
原因:缺少转换为UTF-8的插件
目的:安装ConvertToUTF8插件包
第一步:安装能自动安装插件的插件,百度“Codecs33”,然后按照步骤可以得到以下一段代码:
import urllib.request,os,hashlib; h = 'eb2297e1a458f27d836c04bb0cbaf282' + 'd0e7a30980927
- 概念了解:CGI,FastCGI,PHP-CGI与PHP-FPM
geeksun
PHP
CGI
CGI全称是“公共网关接口”(Common Gateway Interface),HTTP服务器与你的或其它机器上的程序进行“交谈”的一种工具,其程序须运行在网络服务器上。
CGI可以用任何一种语言编写,只要这种语言具有标准输入、输出和环境变量。如php,perl,tcl等。 FastCGI
FastCGI像是一个常驻(long-live)型的CGI,它可以一直执行着,只要激活后,不
- Git push 报错 "error: failed to push some refs to " 解决
hongtoushizi
git
Git push 报错 "error: failed to push some refs to " .
此问题出现的原因是:由于远程仓库中代码版本与本地不一致冲突导致的。
由于我在第一次git pull --rebase 代码后,准备push的时候,有别人往线上又提交了代码。所以出现此问题。
解决方案:
1: git pull
2:
- 第四章 Lua模块开发
jinnianshilongnian
nginxlua
在实际开发中,不可能把所有代码写到一个大而全的lua文件中,需要进行分模块开发;而且模块化是高性能Lua应用的关键。使用require第一次导入模块后,所有Nginx 进程全局共享模块的数据和代码,每个Worker进程需要时会得到此模块的一个副本(Copy-On-Write),即模块可以认为是每Worker进程共享而不是每Nginx Server共享;另外注意之前我们使用init_by_lua中初
- java.lang.reflect.Proxy
liyonghui160com
1.简介
Proxy 提供用于创建动态代理类和实例的静态方法
(1)动态代理类的属性
代理类是公共的、最终的,而不是抽象的
未指定代理类的非限定名称。但是,以字符串 "$Proxy" 开头的类名空间应该为代理类保留
代理类扩展 java.lang.reflect.Proxy
代理类会按同一顺序准确地实现其创建时指定的接口
- Java中getResourceAsStream的用法
pda158
java
1.Java中的getResourceAsStream有以下几种: 1. Class.getResourceAsStream(String path) : path 不以’/'开头时默认是从此类所在的包下取资源,以’/'开头则是从ClassPath根下获取。其只是通过path构造一个绝对路径,最终还是由ClassLoader获取资源。 2. Class.getClassLoader.get
- spring 包官方下载地址(非maven)
sinnk
spring
SPRING官方网站改版后,建议都是通过 Maven和Gradle下载,对不使用Maven和Gradle开发项目的,下载就非常麻烦,下给出Spring Framework jar官方直接下载路径:
http://repo.springsource.org/libs-release-local/org/springframework/spring/
s
- Oracle学习笔记(7) 开发PLSQL子程序和包
vipbooks
oraclesql编程
哈哈,清明节放假回去了一下,真是太好了,回家的感觉真好啊!现在又开始出差之旅了,又好久没有来了,今天继续Oracle的学习!
这是第七章的学习笔记,学习完第六章的动态SQL之后,开始要学习子程序和包的使用了……,希望大家能多给俺一些支持啊!
编程时使用的工具是PLSQL