二、深度学习的参数调优及优化

前言

深度学习领域由于在解决不同的问题上所用的模型都是不尽相同的，但有一些通用化的方法来解决问题。这一章节将讨论如何有效运作神经网络，内容涉及超参数调优，如何构建数据，以及如何确保优化算法快速运行，从而使学习算法在合理时间内完成自我学习。
另：本系列的所有代码都以jupyter notebook格式托管到github上，大家可以去下载看下
https://github.com/Wangzg123/KerasDeepLearningDemo

一、正则化

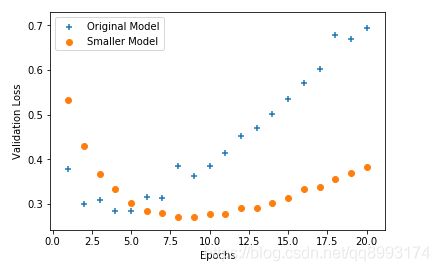
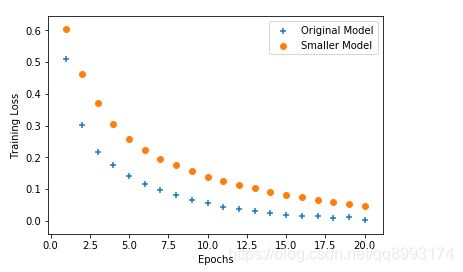
我们以两个图像来解释下深度学习领域的大敌——过拟合，过拟合指的是模型在训练集上表现良好，但是在别的数据集上却表现得差强人意，往往随着训练次数的加深，模型会越来越差。如下示这两个模型都有这样的特点，随着训练批次的增加，在训练集上的损失率越来越少，而在别的数据集上的损失率却越来越高。那么这个时候就可以通过正则化的几种方法来减少过拟合问题。

1、数据集划分

在开始讲正则化之前，我们先来讨论讨论一下数据集划分的问题。通常我们会将数据集划分为训练集，验证集和测试集
在机器学习发展的小数据量时代（1万以下），常见做法是将所有数据三七分，就是人们常说的 70%训练集集， 30%测试集，如果没有明确设置验证集，也可以按照 60%训练， 20%验证和 20%测试集来划分。这是前几年机器学习领域普遍认可的最好的实践方法。
而在大数据集上我们通常将样本分成训练集，验证集和测试集三部分，数据集规模相对较小，适用传统的划分比例，数据集规模较大的，验证集和测试集要小于数据总量的 20%或 10%。 至于为什么要划分验证集，以下摘自《python深度学习》一书，这本书很好的说明了划分验证集的好处

2、几种正则化方式的实现

我们这里通过一个keras自带的IMDB数据集（根据电影评语是否好评）的例子来看下几种正则化的实现方式，并且通过对比不同模型损失率图形来看下这几种正则化带来的直观理解。

减少网络大小和早停法（early stop）

如果你的模型很复杂，但是问题却很简单（如上述的IMDB），那么减少网络大小是可以减少过拟合的一种手段

# 导入数据集集必要的库
from keras.datasets import imdb
import numpy as np
from keras import models
from keras import layers
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
# 将数据集模型向量化函数
def vectorize_sequences(sequences, dimention=10000):
    results = np.zeros((len(sequences), dimention))
    for i, sequence in enumerate(sequences):
        results[i, sequence] = 1.
    return results
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
# 划分数据集合训练集
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]
# 定义一个最原始的模型
def origin_model():
    model = models.Sequential()
    model.add(layers.Dense(16, activation='relu', input_shape = (x_val.shape[1], )))
    model.add(layers.Dense(16, activation='relu'))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
    return model
# 定义一个小一点的模型
def small_model():
    model = models.Sequential()
    model.add(layers.Dense(4, activation='relu', input_shape = (x_val.shape[1], )))
    model.add(layers.Dense(4, activation='relu'))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
    return model
# 开始训练
his_origin = origin_model().fit(partial_x_train, partial_y_train, epochs=20, batch_size=512, validation_data=(x_val, y_val))
# 分别开始训练
his_small = small_model().fit(partial_x_train, partial_y_train, epochs=20, batch_size=512, validation_data=(x_val, y_val))
# 获取下训练中的数据
his_origin_dict = his_origin.history
his_small_dict = his_small.history
# 导入绘图模块
import matplotlib.pyplot as plt
# 对比下几个模型的参数
origin_validation_loss_value = his_origin_dict['val_loss']
small_validation_loss_value = his_small_dict['val_loss']
Epochs = range(1, len(origin_validation_loss_value) + 1)
# 验证集损失率对比
plt.scatter(Epochs, origin_validation_loss_value, marker='+', label='Original Model')
plt.scatter(Epochs, small_validation_loss_value, marker='o', label='Smaller Model')
plt.xlabel('Epochs')
plt.ylabel('Validation Loss')
plt.legend()
plt.show()

绘制的图像如下示，可以看到相对于原来的模型，减少网络模型可以有效的减慢损失值的大小，另外一个关于早停法的也相对于提一下（因为我觉得早停法不好），我们通过看到橘色的模型在Epochs = 10的时候损失值最小，那么我们可以把轮训的次数设置在10，这样得到相对好一点的模型，这就是早停法。

L2正则化

权重正则化是一种常见的降低过拟合的方法就是强制让模型权重只能取较小的值，从而限制模型的复杂度，这使得权重值的分布更加规则。这种方法叫作权重正则化。正则化有L1正则化和L2正则化。
L1 正则化（L1 regularization）：添加的成本与权重系数的绝对值［权重的 L1 范数（norm）］成正比
L2 正则化（L2 regularization）：添加的成本与权重系数的平方（权重的 L2 范数）成正比。神经网络的 L2 正则化也叫权重衰减（weight decay）。不要被不同的名称搞混，权重衰减与 L2 正则化在数学上是完全相同的。

# 以下代码承接上面
# L2权重正则化模型
def L2_model():
    model = models.Sequential()
    model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001), activation='relu', input_shape=(x_val.shape[1], )))
    model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001), activation='relu'))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
    return model
# L2正则化开始训练
his_L2 = L2_model().fit(partial_x_train, partial_y_train, epochs=20, batch_size=512, validation_data=(x_val, y_val))
his_L2_dict = his_L2.history
# 绘制L2正则化曲线
L2_validation_loss_value = his_L2_dict['val_loss']
plt.scatter(Epochs, origin_validation_loss_value, marker='+', label='Original Model')
plt.scatter(Epochs, L2_validation_loss_value, marker='o', label='L2-regularized Model')
plt.xlabel('Epochs')
plt.ylabel('Validation Loss')
plt.legend()
plt.show()

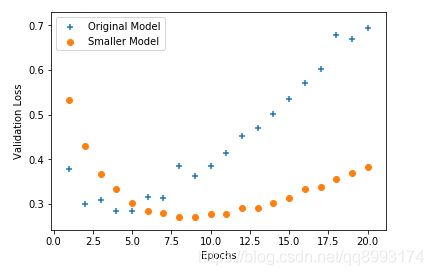
绘制的图像如下示，可以看到相对于原来的模型，橘色点的模型损失率比较缓和，可以提升模型的泛化能力

Dropout正则化

dropout 是神经网络最有效也最常用的正则化方法之一，它指的是对某一层使用 dropout，就是在训练过程中随机将该层的一些输出特征舍弃（设置为 0）。以下是keras实现dropout的形式

# 以下代码承接上面
# Dropout正则化
def Dropout_model():
    model = models.Sequential()
    model.add(layers.Dense(16, activation='relu', input_shape=(x_val.shape[1], )))
    model.add(layers.Dropout(0.5))
    model.add(layers.Dense(16, activation='relu'))
    model.add(layers.Dropout(0.5))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
    return model
# 开始训练
his_dropout = Dropout_model().fit(partial_x_train, partial_y_train, epochs=20, batch_size=512, validation_data=(x_val, y_val))
his_dropout_dict = his_dropout.history
# 绘制Dropout正则化曲线
dropout_validation_loss_value = his_dropout_dict['val_loss']
plt.scatter(Epochs, origin_validation_loss_value, marker='+', label='Original Model')
plt.scatter(Epochs, dropout_validation_loss_value, marker='o', label='Dropout-regularized Model')
plt.xlabel('Epochs')
plt.ylabel('Validation Loss')
plt.legend()
plt.show()

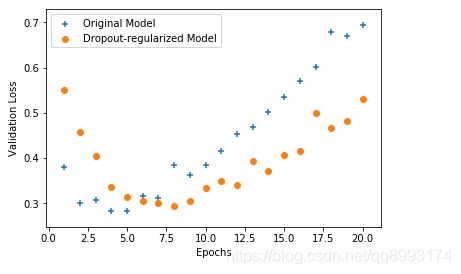
绘制的图像如下示，可以看到相对于原来的模型，橘色点的模型损失率比较缓和，可以提升模型的泛化能力

二、优化算法

上面的模型我们其实已经用了rmsprop优化算法了，其实这种优化算法也是梯度下降法的变式，只不过是在将学习率做一个加权的操作使得模型更快的收敛（当然具体的做法没那么简单），下面来介绍下几种梯度下降法和优化器

1、几种梯度下降法

这里分别简要介绍下BGD，SGD，MBGD，更多介绍请查阅 梯度下降法的三种形式-BGD、SGD、MBGD

批量梯度下降法BGD

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新。我们的目的是要误差函数尽可能的小，即求解weights使误差函数尽可能小。首先，我们随机初始化weigths，然后不断反复的更新weights使得误差函数减小，直到满足要求时停止。这里更新算法我们选择梯度下降算法，利用初始化的weights并且反复更新weights。

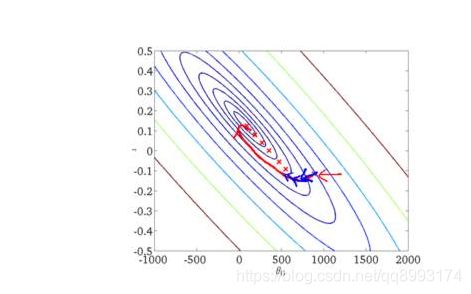
随机梯度下降法SGD

随机梯度下降是通过每个样本来迭代更新一次，对比上面的批量梯度下降，迭代一次需要用到所有训练样本（往往如今真实问题训练数据都是非常巨大），一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

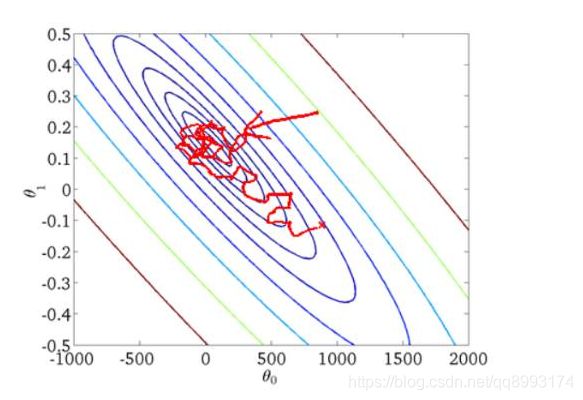
min-batch 小批量梯度下降法MBGD

我们从上面两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？既算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。我们假设每次更新参数的时候用到的样本数为10个（不同的任务完全不同，这里举一个例子而已）

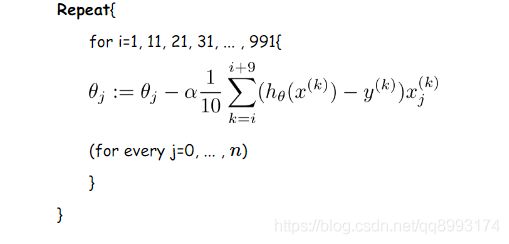
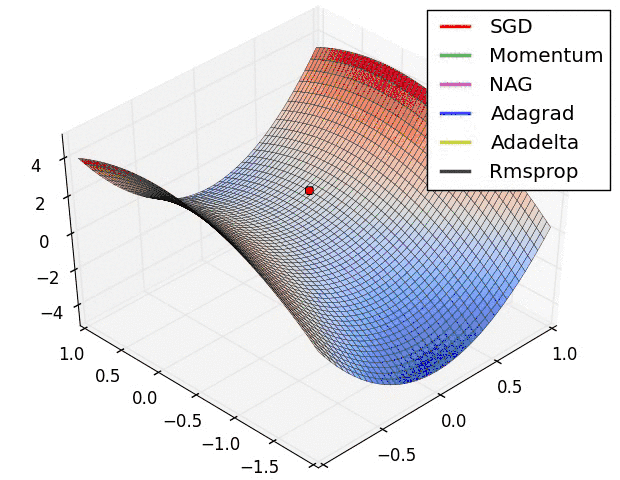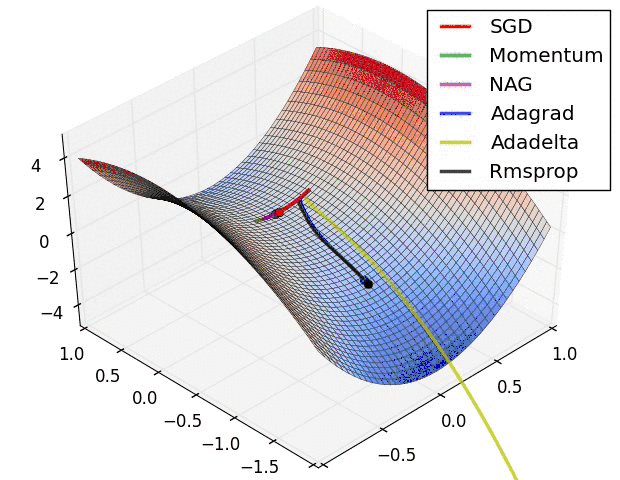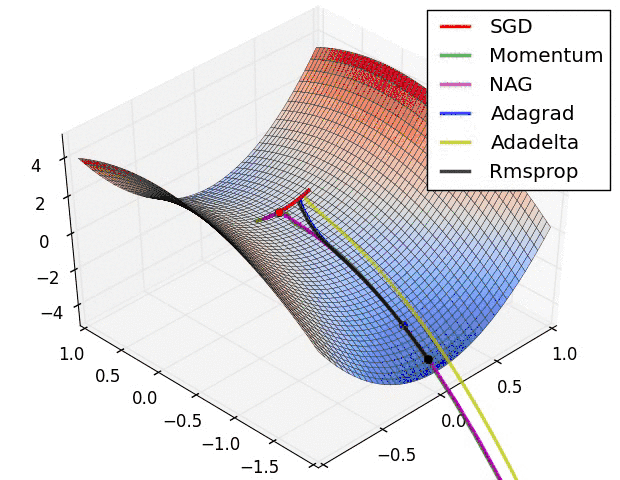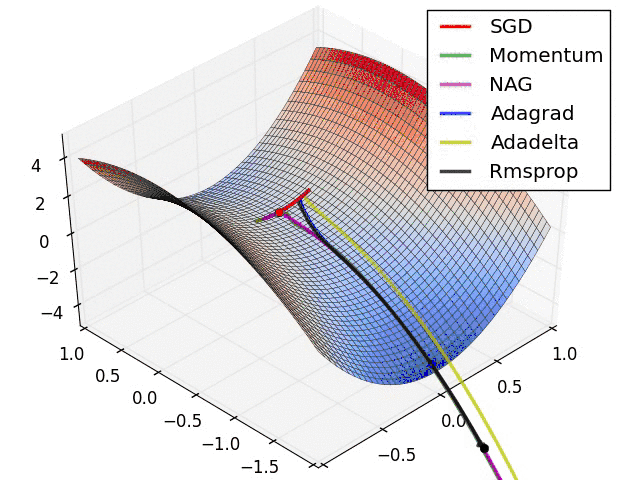
2、Momentum、Rmsprop及Adam优化算法

我们之前谈论的下降法的学习率都是固定，那么固定的学习率其梯度下降的步长是一定的，这样就可能在导致收敛得比较慢，西面有这几种变式来解决学习率的问题，更多的可以参考这篇文章，我觉得写的挺好。《【深度学习】深入理解优化器Optimizer算法（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）》

3、批量归一化（Batch norm）

**标准化（normalization）**是一大类方法，用于让机器学习模型看到的不同样本彼此之间更加相似，这有助于模型的学习与对新数据的泛化。最常见的数据标准化形式就是将数据减去其平均值使其中心为 0，然后将数据除以其标准差使其标准差为 1。实际上，这种做法假设数据服从正态分布（也叫高斯分布），并确保让该分布的中心为 0，同时缩放到方差为 1。
**批标准化（batch normalization）**即使在训练过程中均值和方差随时间发生变化，它也可以适应性地将数据标准化。批标准化的工作原理是，训练过程中在内部保存已读取每批数据均值和方差的指数移动平均值。批标准化的主要效果是，它有助于梯度传播（这一点和残差连接很像），因此允许更深的网络。对于有些特别深的网络，只有包含多个 BatchNormalization 层时才能进行训练。例如， BatchNormalization 广泛用于 Keras 内置的许多高级卷积神经网络架构，比如 ResNet50、 Inception V3 和Xception。——摘自《python深度学习》一书

三、总结

我们上面介绍了几种正则化的方式来减少过拟合，分别是减少网络大小，L2正则化（权重衰减）和Dropout，简单提到早停法（由于早停法根本没有解决模型的问题，只是适当的停止，这样其实没什么太多好处），也介绍了几种梯度下降法的形式，其中我们训练用得最多的就是小批量梯度下降法，上面的模型都是基于小批量梯度下降法来实现的，最后还提到梯度下降法的几种优化器，目前用得最多的就是Adam，我并没有特别深究里面的实现方式，只是知道Adam优化器是性能最好的。这就是这篇博客的主要内容。