深入浅出零知识证明（一）：Schnorr协议

       最近在学习零知识证明，因为内容很多并且难度也大，想根据自己的学习路线做一系列总结，这是第一篇文章，主要介绍零知识证明的一些重要概念和思想，可以对零知识证明有直观的理解，然后讲解一个经典简洁的零知识证明安全协议Schnorr协议。

       本篇文章主要包含四个方面，首先来总体介绍一下零知识证明，然后以地图三染色问题为例，体现零知识证明思想，然后分析交互式Schnorr协议和非交互式Schnorr协议。

1.零知识证明概述

     ·简介

       零知识证明(Zero-Knowledge Proof)，是由S.Goldwasser、S.Micali及C.Rackoff在20世纪80年代初提出的。证明者能够在不向验证者提供任何有用的信息的情况下，使验证者相信某个论断是正确的。零知识证明实质上是一种涉及两方或更多方的协议，即两方或更多方完成一项任务所需采取的一系列步骤。

    ·概念

      “P”表示 “证明者(Proofer)”：作为零知识证明的参与方，他在证明命题真实性的同时，不会泄漏任何相关信息。

      “V”表示 “验证者(Verifier)”：作为零知识证明的另一参与方，验证证明者提出的命题以及对应的证明是不是正确。

      “承诺阶段(Commit)”：证明者针对命题做出承诺，并等待验证者提出挑战并进行验证。

      “挑战阶段(Challenge)”：验证者选择随机数，对提出的承诺进行挑战。

      “回应挑战阶段(Response)”：证明者将收到的随机数并结合给出的承诺，返回挑战的回应。

      “验证阶段(Verify)”：验证者验证，挑战的回应是否正确，错误的话那就证明失败，如果成功就可进行下一次挑战，直到可以相信的概率达到验证者接受的条件，这样就证明成功。

    ·性质

       在零知识证明中，需要满足三个性质：

       正确性。没有人能够假冒P使这个证明成功。如果不满足这条性质，也就是P不知道“知识”，再怎么证明，V也很难相信P拥有正确的知识。

       完备性。如果P和V都是诚实的，并证明过程的每一步都进行正确的计算，那么这个证明一定是成功的。也就是说如果P知道“知识”，那么V会有极大的概率相信P。

       零知识性。证明执行完之后，V只获得了“P拥有这个知识”这条信息，而没有获得关于这个知识本身的任何信息。

    ·应用

       数据的隐私保护：在隐私场景中，根据零知识性，不泄漏交易的接收方，发送方，交易余额等细节的前提下，证明区块链上的资产转移是有效的。再比如买保险的时候，保险公司需要了解是否患有某种疾病，但是我不想让保险公司知道我的全部病历信息，那我可以证明给保险公司看，我没有相关疾病就足够了。

        计算压缩与区块链扩容：在当前的区块链架构中，同样的计算会被重复多次，比如签名的校验，交易合法性校验，智能合约的执行等等。这些计算过程都可以被零知识证明技术进行压缩。比如以太坊采用 zkSNARK，带来几十倍的性能提升。

        端到端的通讯加密：用户可以互相通信，但是消息记录不会完全暴露在服务器上，同时消息也可以按照服务器的要求，出示相应的零知识证明，比如消息的来源、与发送的目的地。

        身份认证：用户可以向网站证明，他拥有私钥，网站并不需要知道私钥的内容，可以通过验证这个零知识证明， 确认用户的身份。

        去中心化存储：服务器可以向用户证明他们的数据被妥善保存，并且不泄露数据的内容。

2.举例：地图三染色问题

   ·地图三染色问题

         三染色问题：假设存在一个地图，不同城市之间修建一些道路，三染色问题即为是否存在一种染色方式，使得每个城市都用特定的三种颜色之一表示，并且任意有道路相连的两个城市都不是相同的颜色。

        下面设计一个交互协议： Alice是「证明者」，Bob是「验证者」

        Alice拥有一个对特定地图的三染色方案，希望在不泄漏任何信息的条件下向Bob证明自己拥有该方案。

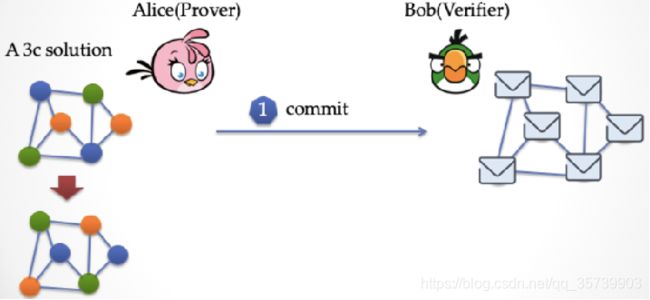
    1. 承诺阶段

        首先，在承诺阶段，Alice 先要对染过色的图进行一些「变换」，把颜色进行置换，例如把所有的蓝色变成绿色，绿色变成橙色，橙色变成蓝色。这样 Alice 得到了一个新的染色答案，这时候她把新图的每一个顶点都用纸片盖上，然后出示给 Bob 看。

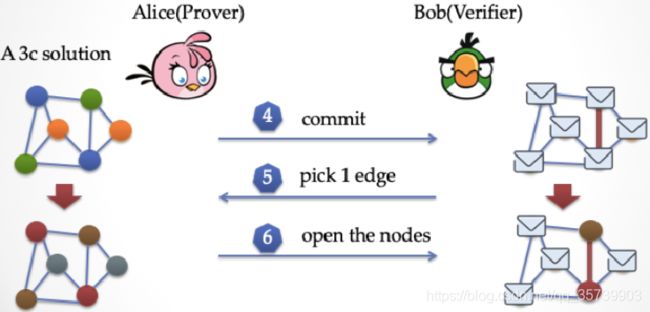
      2. 挑战阶段

       下面进入挑战阶段，bob要挑战Alice是否真的知道答案，但是他不能直接打开所有信封，只能随机选择任意一条边，要求Alice打开相邻两个节点的纸片进行验证两个顶点的颜色是否相同。

      3. 回应挑战阶段

         然后进入回应挑战阶段，假设 Bob 挑选的是最下面的一条边。Alice打开Bob指定的两个节点，作为对挑战的回应，让 Bob 检查，发现这两个顶点的颜色是不同的，那么 Bob 认为这次检验正确。但是Bob 只看到了图的局部，一次挑战不能让他信任，但是多次挑战可能让Bob获取到Alice全部的染色方案，极端情况就是Bob查看了所有边的相邻节点颜色，从而完全重构出染色方案。

      4. 重复过程

       所以要对上述三个阶段进行多次重复，每次在承诺阶段Alice都会将染色方案进行一次随机置换，使得Bob每次验证，只能得到指定的两个相邻节点染色是否相等的信息。随着重复的次数足够多，Bob有极大概率相信Alice拥有一个正确的染色方案。但是Bob 每次看到的局部染色情况，都是 Alice 变换过后的结果，无论 Bob 看多少次，都不能拼出一个完整的三染色答案出来。Bob 在这个过程中，虽然获得了很多「信息」，但是却没有获得真正的「知识」。

       通过这个例子，对零知识证明可以有直观的了解。接下来，介绍一个简洁，用途广泛的零知识证明系统 —— Schnorr 协议。

 3.交互式Schnorr协议

        Schnorr机制是一种基于离散对数难题的零知识证明机制。证明者声称知道一个密钥x的值，通过使用Schnorr加密技术，可以在不揭露x的情况下，向验证者证明对x的知情权。可用于证明你有一个私钥但是不披露私钥的内容。

       原始的Schnorr机制是一个交互式的机制。Schnorr中涉及到的技术有哈希函数的性质、椭圆曲线的离散对数难题。

    （椭圆曲线的离散对数难题是指，已知椭圆曲线E和点G，随机选择一个整数d，容易计算椭圆曲线上另一点Q=d*G，但是给定的Q和G来计算d就非常困难。）

       假设Alice 拥有一个秘密数字，a，我们可以把这个数字当成「私钥: sk」，然后把它「映射」到椭圆曲线群上的一个点 a*G，简写为 aG。这个点我们把它当做「公钥: PK」。

       Schnorr 协议充分利用了有限域和循环群之间单向映射，实现了简洁的零知识证明安全协议：Alice 向 Bob 证明她拥有 PK 对应的私钥 sk，那么如何证明呢。

        交互式Schnorr协议的流程分为三步：

        第一步：为了保证零知识，Alice 需要先产生一个随机数r，这个随机数是用来保护私钥无法被 Bob 抽取出来，会映射到椭圆曲线群上的点rG上，记为R发送给Bob。

        第二步：Bob 要提供一个随机数进行挑战，把它称为 c。

        第三步：Alice 根据挑战数计算 z = r + a * c，然后把 z 发给 Bob，Bob通过式子进行检验：z*G ?= R + c*PK

        由于z=r+c*sk，等式两边添加相同的生成元可得：z*G= rG + c*(aG)=c*PK+R。就可以验证Alice确实拥有私钥sk，但是验证者Bob并不能得到私钥sk的值，因此这个过程是零知识的，并且是交互式的。

        由于椭圆曲线上的离散对数问题，知道R和G的情况下通过R=r*G解出r是不可能的，所以保证了r的私密性。

        但是，整个过程是在证明者和验证者在私有安全通道中执行的。这是由于协议存在交互过程，只对参与交互的验证者有效，其他不参与交互的验证者，无法判断整个过程是否存在串通的舞弊行为，一旦两个验证者相互串通，交换自己得到的值，便可以推出私钥。因此，是无法公开验证的。

        进一步分析，为什么需要验证者回复一个随机数c呢？这是为了防止Alice造假。

        如果Bob不回复一个c，就变成一次性交互。由于椭圆曲线上的离散对数问题，知道PK和G的情况下通过PK = a * G接触a是不可能的，所以保证了a的私密性。

        但是这种方案是存在问题的，a和r都是Alice自己生成的，她知道Bob会用PK和R相加然后再与z * G进行比较。所以她完全可以在不知道a的情况下构造：R = r * G - PK 和 z = r。 这样Bob的验证过程就变成：z * G ?== PK + R ==> r * G ?== PK + r * G - PK。这是永远成立的，所以这种方案并不正确。

        所以在交互式Schnorr协议中存在的私钥泄露问题，使得算法无法在公开的环境下使用。

        可以将原始的交互式协议转变为非交互式协议来解决这个问题！

       下面来看，如何把一个三步的 Schnorr 协议变成一步。

 4.非交互式Schnorr协议

         回顾一下交互式Schnorr 协议的第二步，Bob 需要给出一个随机的挑战数 c，这里我们可以让 Alice 用下面这个式子来计算这个挑战数，从而达到去除协议第二步的目的。

         c = Hash(PK, R) 。

         其中 R 是 Alice 发给 Bob 的椭圆曲线点，PK 是公钥。

         这个式子达到了两个目的：
         第一个，Alice 在产生承诺 R 之前，没有办法预测 c，即使 c 最终是 Alice 生成的。

         第二个，c 通过 Hash 函数计算，会均匀分布在一个整数域内，可以作为一个随机数。

         Hash 函数是「单向」的，这样一来，虽然 c 是 Alice 计算的，但是 Alice 并没有能力实现通过挑选 c 来作弊。因为只要 Alice 一产生 R， c 就相当于固定下来了。

         这样，就把三步Schnorr协议合并为一步。Alice可直接发送（R，z），因为Bob拥有Alice的公钥PK，于是Bob可自行计算出c。然后验证z*G?=R+c*PK。

       如图，利用 Hash 函数，把三步 Schnorr 协议合并为了一步。Alice 可以直接发送：(R, c, z)。又因为 Bob 拥有 PK，于是 Bob 可以自行计算出 c，于是 Alice 可以只发送 (R, z) 即可。

       ·Alice：均匀随机选择r，并依次计算 R=r*G c=Hash(R,PK) z=r+c*sk

       ·Alice：生成证明(R,z)

       ·Bob(或者任意一个验证者)：计算e=Hash(PK,R)

       ·Bob(或者任意一个验证者)：验证z*G?==R+c*PK

 5.Schnorr用于数字签名

        Schnorr 协议可以用于数字签名。

        首先，为了保证攻击者不能随意伪造签名，使用离散对数难题和Hash函数满足抗第二原象（防碰撞）作为安全假设。

        提出数字签名的出发点有两个：

        一是，接收方希望证实消息在传递过程中没有被篡改；

        二是，希望确认发送者的身份，可以理解为发送者有一个私钥，并且私钥和这条消息进行关联计算。

        首先要证明发送者的身份，这正是Schnorr协议的功能，能够向对方证明「我拥有私钥」这个陈述。并且这个证明过程是零知识的，不泄露关于「私钥」的任何知识。而c=Hash(m,R)可以保证发送者与信息相关联。

        上图就是Schnorr签名方案。在这里还有一个优化，Alice发给Bob的内容不是(R,z)而是(c,z)，这是因为R可以通过c,z计算出来。

        分析下优化的原理，令n是有限域大小的位数。假设采用了非常接近2^256的有限域，也就是说z是256bit，那么椭圆曲线群的大小也差不多要接近256bit，这样一来，把2^256开平方根后就是2^128，所以说256bit椭圆曲线群的安全性只有128bit。那么，挑战数c也只需要128bit就足够了。这样Alice发送c要比发送R要更节省空间，而后者至少需要256bit。c只需要128bit。相比ECDSA签名方案来说，可以节省1/4的空间。