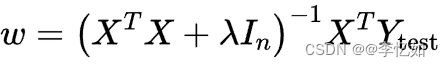机器学习——LR(线性回归)、LRC(线性回归分类)与人脸识别
目录
系列文章目录
一、LR的概念、原理与LR用于简单数据的预测
1.LR简介
2.LR算法模型
3.LR用于简单数据的预测
二、LRC的简介与算法流程
1.LRC(线性回归分类)简介
2.LRC算法流程
三、LRC及其各种优化模型用于人脸识别
1. 数据导入与处理
2.人脸识别与分类
2.1.经典线性回归分类用于人脸识别
2.2.岭回归用于人脸识别
2.3.lasso回归用于人脸识别
2.4.分块LRC用于人脸识别
2.5 回归部分代码整合
3.多种回归在人脸识别的对比
4.新线性回归设计、实践、比较
5.其他
5.1 内部函数定义
5.2 数据集及资源
5.3 参考资料
总结
系列文章目录
本系列博客重点在机器学习的概念原理与代码实践,不包含繁琐的数学推导(有问题欢迎在评论区讨论指出,或直接私信联系我)。
第一章 机器学习——PCA(主成分分析)与人脸识别_@李忆如的博客-CSDN博客
第二章 机器学习——LDA (线性判别分析) 与人脸识别_@李忆如的博客-CSDN博客
第三章 LR(线性回归)、LRC(线性回归分类)与人脸识别
梗概
本篇博客主要介绍LR(线性回归)、LRC(线性回归分类)并将LR用于简单数据的预测,LRC及其各种优化模型(岭(脊)回归、lasso回归、分块LRC)用于人脸识别,且自行设计了一个全新的线性回归算法用于人脸识别并与经典LR做比较(内附数据集与matlab代码)
一、LR的概念、原理与LR用于简单数据的预测
1.LR简介
回归分析是指一种预测性的建模技术,主要是研究自变量和因变量的关系。LR(线性回归)为最基础的一种回归算法。用线(面)等模型对于现有相对线性的数据进行较小损失的拟合,并使拟合出的模型可较好预测数据。
2.LR算法模型
经典的LR解决问题可划分为以下步骤
① 将数据集导入,进行变量的筛选与控制
② 对正态性分布的数据做散点图与相关分析
③ 通过最小化损失函数来确定参数,得到(拟合)回归方程(利用正规方程计算w 或最小二乘 或梯度下降)
④ 不断检验模型,优化参数,得到最优的回归方程
⑤ 使用回归方程做预测
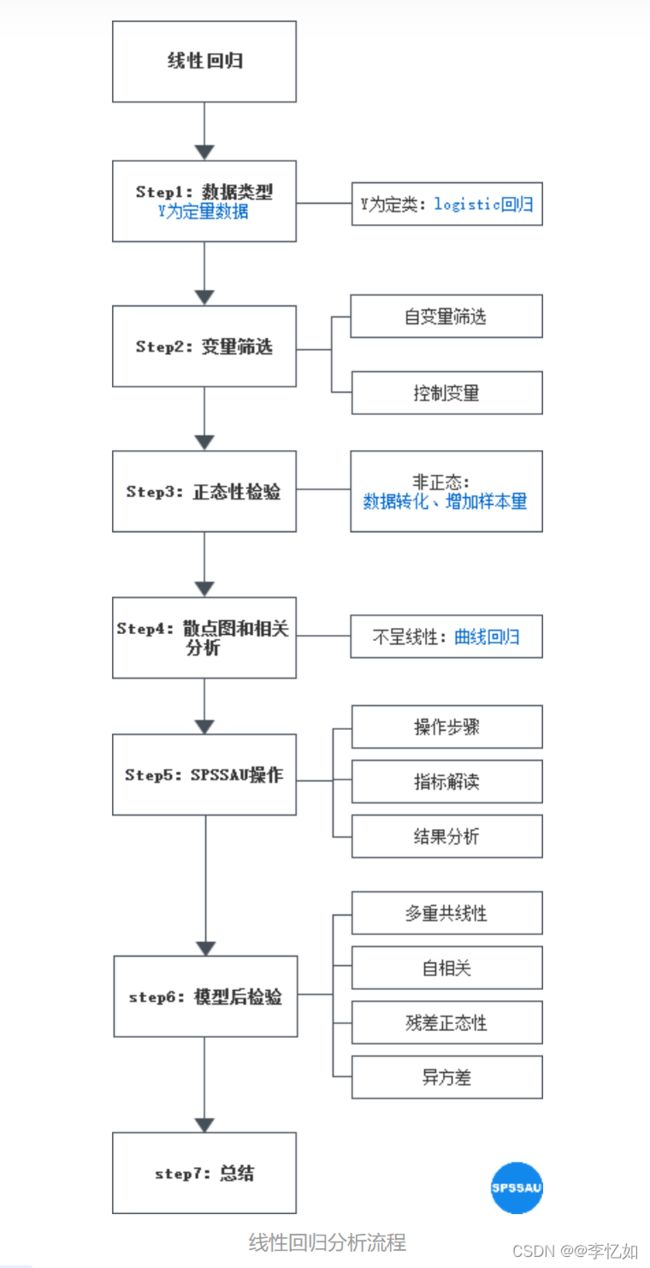
图1 线性回归分析详细流程
Tips:对线性回归数学原理、最小二乘法、梯度下降、正归方程的数学分析与推导感兴趣的详见:机器学习算法——线性回归(超级详细且通俗)_一只认真的菜狗的博客-CSDN博客_线性回归
3.LR用于简单数据的预测
① 问题描述:探究学生成绩与学生学习时间的关系
② 线性回归实现:将学习时间作为变量,成绩作为预测值,建立回归方程,并用最小二乘法最小化损失函数,得到回归方程并验证,验证后用其预测。
③ 核心代码如下:
x=[23.80,27.60,31.60,32.40,33.70,34.90,43.20,52.80,63.80,73.40];
y=[41.4,51.8,61.70,67.90,68.70,77.50,95.90,137.40,155.0,175.0];
figure
plot(x,y,'r*') %作散点图(制定横纵坐标)
xlabel('x(学生学习时间)','fontsize',12)
ylabel('y(学生成绩)','fontsize',12)
set(gca,'linewidth',2)
%采用最小二乘拟合
Lxx=sum((x-mean(x)).^2);
Lxy=sum((x-mean(x)).*(y-mean(y)));
b1=Lxy/Lxx;
b0=mean(y)-b1*mean(x);
y1=b1*x+b0; %线性方程用于预测和拟合
hold on
plot(x,y1,'linewidth',2);
m2=LinearModel.fit(x,y); %函数进行线性回归数据拟合后,回归模型绘图如下:
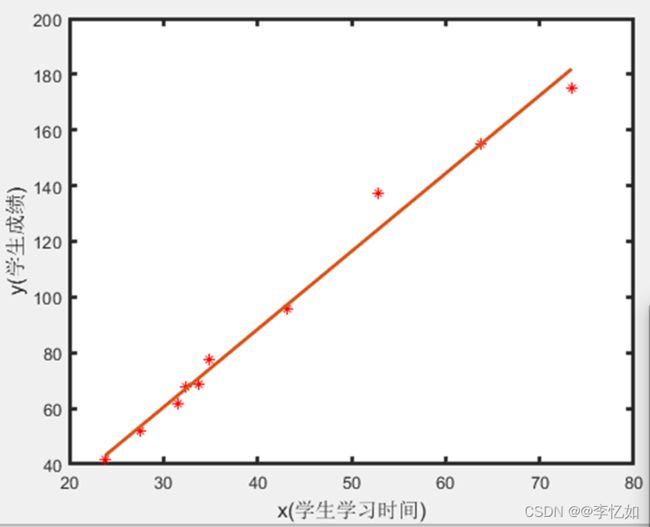
图2 LR用于简单数据预测回归方程绘图
分析:分析上图,可看出模型对数据拟合较好,预测相对线性。如需预测不在图中的数据,只需将对应学习时间作为x代入回归模型(方程)中即可。
二、LRC的简介与算法流程
1.LRC(线性回归分类)简介
LRC:即使用LR进行分类任务(如人脸识别,给出某人脸属于哪一类人(一个人为一类))
2.LRC算法流程
① 将数据集导入并分类
② 读取每个类数据进行线性回归,划分训练集与测试集
③ 利用正规方程计算w(或最小二乘 或梯度下降),通过最小化损失函数来确定参数,得到(拟合)回归方程
Tips:此处y为对应需要分类的单个数据
④ 利用回归方程预测数据
⑤ 计算出预测数据与真实数据的距离(损失),并将最小距离对应类别作为预测类别输出
三、LRC及其各种优化模型用于人脸识别
1. 数据导入与处理
利用imread批量导入人脸数据库,或直接load相应mat文件,并在导入时不断将人脸拉成一个个列向量组成reshaped_faces,并取出n%作为测试数据,剩下100-n%作为训练数据,重复此步骤,将导入数据抽象成框架,可以匹配不同数据集的导入(本实验框架适配ORL、AR、FERET数据集)。
Tips:代码可见笔者上一篇文章(LDA与人脸识别),基本一致。
2.人脸识别与分类
Tips:前四部分讲述LRC及其优化模型的算法流程、核心流程、分析,完整代码整合见第五部分。
2.1.经典线性回归分类用于人脸识别
① 算法流程:与二.2中的算法流程类似,将数据集导入并分类,读取每个类数据进行线性回归,划分训练集与测试集,利用正规方程计算w,预测数据后计算出预测数据与真实数据的距离,并将最小距离对应类别作为预测类别,并与测试集对应的标签作比较,检测(识别)分类是否正确,并得出正确率。
② 核心代码:
% 1.线性回归
w = inv(train_data' * train_data) * train_data' * totest;
img_predict = train_data * w; % 计算预测图片
% 分类、预测过程(各种分类都类似)
% show_face(img_predict,row,column); %预测人脸展示
dis = img_predict - totest; % 计算误差
distest = [distest,norm(dis)]; % 计算欧氏距离
% 取出误差最小的预测图片 并找到他对应的标签 作为预测结果输出
end
[min_dis,label_index] = min(distest); % 找到最小欧氏距离下标(预测类)
if label_index == totest_index
count_right = count_right + 1;
else
fprintf("预测错误:%d\n" ,(i + 1) * (k - train_num_each));
end
end③ 分析:w的计算(最小化损失函数得最优参数)、计算预测图片的方法差异造就了不同方法。其中,对于数据的过拟合、关键矩阵不可逆现象,引入岭回归与lasso回归;对于数据遮挡问题,引入分块LRC。
2.2.岭回归用于人脸识别
① 算法核心:对经典线性回归加入L2正则化
② 核心代码:
% 2.岭回归
rr_data = (train_data' * train_data) + eye(train_num_each)*10^-6;
w = inv(rr_data) * train_data' * totest;
img_predict = train_data * w; % 计算预测图片③ 分析:通过正则化扰动,有效地避免了过拟合严重或各变量之间存在多重共线性的问题。
2.3.lasso回归用于人脸识别
① 算法核心:对经典线性回归加入L1正则化
② 核心代码:
% 3.lasso回归
[B,FitInfo] = lasso(train_data , totest);
img_predict = train_data * B + FitInfo.Intercept;Tips:此处使用matlab库中的lasso回归,更详细自定义lasso回归实现与分析见:建模算法系列十九:lasso回归推导附MATLAB源码 - 知乎 (zhihu.com)
③ 分析:一般来说,对于高维的特征数据,尤其线性关系是稀疏的,我们会采用Lasso回归。或者要在一堆特征里面找出主要的特征,那Lasso回归更是首选。
2.4.分块LRC用于人脸识别
① 算法核心:把数据库中每个数据分成M块(本实验将人脸均分四块),对数据中的每块进行LRC,在同一数据的M块min_dis中选出最小值,其对应的块作为分类依据,给出预测分类结果(或使用投票法选出同一数据M块中出现最多的预测分类结果)。
② 核心代码:
%%数据导入部分进行分块(不同分块规则大大影响实验效果,此处以均分四块为例)
for i=1:40
for j=1:10
if(i<10)
a=imread(strcat('C:\Users\hp\Desktop\face\ORL56_46\orl',num2str(i),'_',num2str(j),'.bmp'));
else
a=imread(strcat('C:\Users\hp\Desktop\face\ORL56_46\orl',num2str(i),'_',num2str(j),'.bmp'));
end
a = double(a);
a = mat2cell(a,[row/2,row/2],[column/2,column/2]);
a1 = a{1};
a2 = a{2};
a3 = a{3};
a4 = a{4};
b1 = reshape(a1,row * column / 4,1);
b1=double(b1);
b2 = reshape(a2,row * column / 4,1);
b2=double(b2);
b3 = reshape(a3,row * column / 4,1);
b3=double(b3);
b4 = reshape(a4,row * column / 4,1);
b4=double(b4);
reshaped_faces=[reshaped_faces, b1,b2,b3,b4];
end
end③ 分析:分块线性回归是处理遮挡图像识别的一个有效方法。
2.5 回归部分代码整合
% 回归过程
dimension = row * column;
count_right = 0;
for i = 0:1:people_num - 1
totest_index = i + 1; %取出图片对应标签
%对每一类进行一次线性回归
for k = train_num_each + 1:1:pic_num_of_each
totest = reshaped_faces(:,i*pic_num_of_each + k); %取出每一待识别(分类)人脸
distest = []; %记录距离
for j = 0:1:people_num - 1
batch_faces = reshaped_faces(:,j * pic_num_of_each + 1 :j * pic_num_of_each + pic_num_of_each); %取出每一类图片
% 划分训练集与测试集
%第一次 batch中的前train_num_each个数据作为训练集 后面数据作为测试集合
train_data = batch_faces(:,1:train_num_each);
test_data = batch_faces(:,train_num_each + 1:pic_num_of_each);
% 1.线性回归
w = inv(train_data' * train_data) * train_data' * totest;
img_predict = train_data * w; % 计算预测图片
% 2.岭回归
% rr_data = (train_data' * train_data) + eye(train_num_each)*10^-6;
% w = inv(rr_data) * train_data' * totest;
% img_predict = train_data * w; % 计算预测图片
% 3.lasso回归
% [B,FitInfo] = lasso(train_data , totest);
% img_predict = train_data * B + FitInfo.Intercept;
% 4.权重线性回归(代码有误)
% W = eye(dimension);
% kk = 10^-1;
% for jj = 1:1:dimension
% diff_data = reshaped_faces(j+1,:) - reshaped_faces(jj,:);
% W(jj,jj) = exp((diff_data * diff_data')/(-2.0 * kk^2));
% end
% w = inv(train_data' * W * train_data) * train_data' * W * totest;
% 5.新线性回归(已提前PCA降维)
% rr_data = (train_data' * train_data) +
% eye(train_num_each)*10^-6;
% w = inv(rr_data) * train_data' * test_data; % 改良w
% img_predict = train_data * w; % 计算预测图片
% show_face(img_predict,row,column); %预测人脸展示
dis = img_predict - totest; % 计算误差
distest = [distest,norm(dis)]; % 计算欧氏距离
% 取出误差最小的预测图片 并找到他对应的标签 作为预测结果输出
end
[min_dis,label_index] = min(distest); % 找到最小欧氏距离下标(预测类)
if label_index == totest_index
count_right = count_right + 1;
else
fprintf("预测错误:%d\n" ,(i + 1) * (k - train_num_each));
end
end
end
recognition_rate = count_right / test_sum; 3.多种回归在人脸识别的对比
所用数据集:ORL5646、AR5040、FERET_80
分别在不同数据集中使用经典线性回归、岭回归、lasso回归、分块线性回归进行人脸识别分类,人脸识别率对比如下:
表1 不同回归在不同数据集下的人脸识别率
Tips:表中括号内数字为一类人脸训练,测试数量
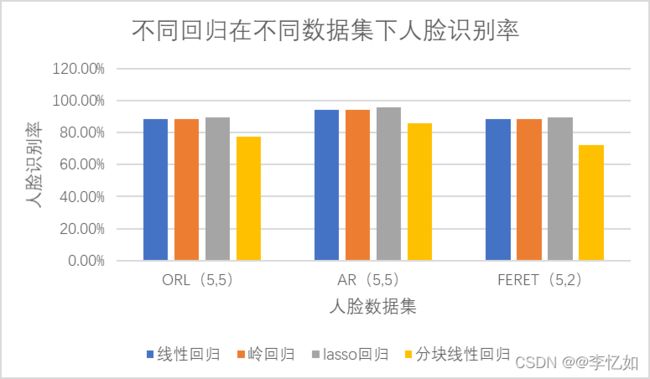
图3 不同回归在不同数据集下的人脸识别率
分析:对上图及上表进行分析,可以得到以下几个结论
a.上述三个数据集中,经典线性回归人脸识别率与岭回归相同。这是由于将一个个人脸拉成列向量,train’ * train的维度较小,矩阵运算不存在奇异值,逆矩阵可逆。
b.上述三个数据集中,lasso回归人脸识别率高于经典线性回归。
c.上述三个数据集中,简单线性回归均优于分块线性回归。这是由于分块逻辑导致的(本实验将人脸均分四块),且使用数据集基本无遮挡,分块线性回归优势不能体现。
4.新线性回归设计、实践、比较
① 经典线性回归缺点:数据规模过大、过拟合严重、各变量之间存在多重共线性、正规方程计算对类内局部结构考虑不够
② 新线性回归设计:在数据预处理时使用PCA降维,对数据压缩。在最小化损失函数的过程中加入L2正则化(岭回归思想),避免过拟合严重、各变量之间存在多重共线性问题,并在正规方程的w运算时使用整个类的测试集而非单一图片,保留一定类内结构。
③ 新线性回归正规方程及核心代码
如②设计,正规方程则变为以下形式:
核心代码如下:
Tips:PCA降维详见完整代码,或参考笔者第一篇文章(PCA与人脸识别)。
% 5.新线性回归(已提前PCA降维)
rr_data = (train_data' * train_data) +
eye(train_num_each)*10^-6;
w = inv(rr_data) * train_data' * test_data; % 改良w
img_predict = train_data * w; % 计算预测图片表2 新老线性回归在不同数据集下的人脸识别率
Tips:表中括号内数字为一类人脸训练,测试数量
图4 新老线性回归在不同数据集下的人脸识别率
分析:对上图及上表进行分析,在ORL与FERET中,新线性回归的人脸识别率高于经典线性回归,在AR中相差无几。由此验证了新线性回归的可行性与正确性,且验证了新线性回归相对线性回归的优越性。
5.其他
5.1 内部函数定义
本实验中将人脸图像展示抽象为函数,函数定义如下:
% 输入向量,显示脸
function fig = show_face(vector, row, column)
fig = imshow(mat2gray(reshape(vector, [row, column])));
end5.2 数据集及资源
本实验所用数据集:ORL5646、AR5040、FERET_80,代码框架可适用多个数据集。
常用人脸数据集如下(不要白嫖哈哈哈)
链接:https://pan.baidu.com/s/12Le0mKEquGMgh5fhNagZGw
提取码:yrnb
LR、LRC完整代码:李忆如/忆如的机器学习 - Gitee.com
5.3 参考资料
1.赖志辉的课
2.线性回归分析思路总结!简单易懂又全面! - 知乎 (zhihu.com)
3.线性回归实现人脸识别——ORL数据集_HeiGe__的博客-CSDN博客_orl人脸数据集
4.周志华《机器学习》
总结
LR作为经典且最基础的回归分析方法,对于线性数据的拟合与预测过程简单,效果优秀,LRC及其多种优化模型在数据分类的任务中也表现优异。且作为一种有监督学习方法(利用了数据的原有信息),LR能得到较好的保留数据信息用于分类。但LR仍存在对异常值很敏感、容易造就过拟合模型、不好刻画非线性问题等等,从而影响实验结果,LR的一些优化模型解决了部分不足,后续博客会分析其他算法优化或解决其他问题。