AI19第二周基础作业

基础作业

1. 画图解释图像卷积滤波的基本原理，并进一步简述常见的图像平滑滤波算法。

基本原理

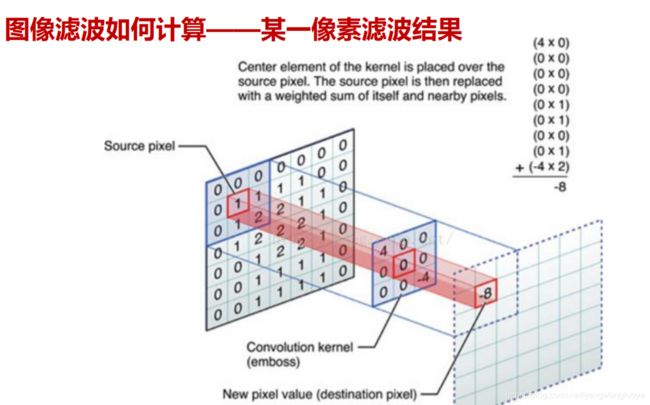
线性滤波是图像处理最基本的方法，我们可以对图像进行处理，产生很多不同的效果。我们有一个二维的滤波器矩阵（卷积核）和一个要处理的二维图像。然后，对于图像的每一个像素点，计算它的邻域像素和滤波器矩阵的对应元素的乘积，然后加起来，作为该像素位置的值。这样就完成了滤波过程（滤波即卷积，由逐点乘积后累加得到）。
(1)滤波器的大小应该是奇数，这样它才有一个中心，例如3x3，5x5或者7x7。
(2)滤波器矩阵所有的元素之和应该要等于1，这是为了保证滤波前后图像的亮度保持不变。
(3)进行计算时，卷积核要进行180^o翻转转换成卷积模板之后进行滤波操作。

其他常见的图像平滑滤波算法

(1)高斯滤波：

dst = cv2.GaussianBlur（ SRC，ksize，sigmaX [，DST [，sigmaY [，borderType ] ] ] ）
图像大多数噪声均属于高斯噪声，因此高斯滤波器应用也较广泛。高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像去噪。
可以简单地理解为，高斯滤波去噪就是对整幅图像像素值进行加权平均，针对每一个像素点的值，都由其本身值和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个用户指定的模板（或称卷积、掩膜）去扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

(2)平均滤波：

dst = cv2.blur(src, ksize[, dst[, anchor[, borderType]]])
均值滤波是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标像素为中心的周围8个像素，构成一个滤波模板，即去掉目标像素本身），再用模板中的全体像素的平均值来代替原来像素值。

(3)中值滤波

dst = cv2.medianBlur（ SRC，ksize [，DST ] ）
中值滤波模板就是用卷积框中像素的中值代替中心值，达到去噪声的目的。这个模板一般用于去除椒盐噪声。前面的滤波器都是用计算得到的一个新值来取代中心像素的值，而中值滤波是用中心像素周围（也可以使他本身）的值来取代他，卷积核的大小也是个奇数。

注：随着中值平滑窗口的增大，椒盐噪声会完全被消除，而且中值滤波后的效果并没有降低边缘的锐利程度，中值平滑具有一定的保边作用。

(4)形态学滤波

dst = cv2.morphologyEx(src, op, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]])
数学形态学滤波基础操作分别为膨胀和腐蚀，开运算为先腐蚀后膨胀，闭运算为先膨胀后腐蚀。一般先进行开运算在进行闭运算可有效去除噪声。

2. 简述边缘检测的基本原理，以及Sobel、LoG和Canny算子的原理差异。

边缘检测基本原理

边缘检测是所有基于边界的图像分割方法的第1步。两个具有不同灰度值的相邻区域之间总存在边缘。边缘是灰度值不连续的结果，这种不连续常可利用求导数方便地检测到，一般常用一阶导数和二阶导数来检测边缘。 常见的边缘剖面有3种:①阶梯状边缘;②脉冲状边缘;③屋顶状边缘。阶梯状的边缘处于图像中两个具有不同灰度值的相邻区域之间，脉冲状主要对应细条状的灰度值突变区域，而屋顶状的边缘上升下降沿都比较缓慢。由于采样的缘故，数字图像中的边缘总有一些模糊，所以这里垂直上下的边缘剖面都表示成有一定坡度。

算子原理

(1)Sobel算子
python中的函数由
dst=cv2.Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]])表示
在边缘检测中，常用的一种模板是Sobel 算子。Sobel 算子有两个，一个是检测水平边缘的 ；另一个是检测垂直边缘的 。与Prewitt算子相比，Sobel算子对于像素的位置的影响做了加权，可以降低边缘模糊程度，因此效果更好。
Sobel算子另一种形式是各向同性Sobel(Isotropic Sobel)算子，也有两个，一个是检测水平边缘的 ，另一个是检测垂直边缘的 。各向同性Sobel算子和普通Sobel算子相比，它的位置加权系数更为准确，在检测不同方向的边沿时梯度的幅度一致。将Sobel算子矩阵中的所有2改为根号2，就能得到各向同性Sobel的矩阵。
由于Sobel算子是滤波算子的形式，用于提取边缘，可以利用快速卷积函数， 简单有效，因此应用广泛。美中不足的是，Sobel算子并没有将图像的主体与背景严格地区分开来，换言之就是Sobel算子没有基于图像灰度进行处理，由于Sobel算子没有严格地模拟人的视觉生理特征，所以提取的图像轮廓有时并不能令人满意。 在观测一幅图像的时候，我们往往首先注意的是图像与背景不同的部分，正是这个部分将主体突出显示，基于该理论，我们给出了下面阈值化轮廓提取算法，该算法已在数学上证明当像素点满足正态分布时所求解是最优的。

(2)LoG算子
python中的公式由
dst = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])表示
拉普拉斯算子是一种高通滤波器，是影像灰度函数在两个垂直方向二阶偏导数之和。在离散数字影像的情况下,直接用影像灰度级的二阶差分代替连续情形下的二阶偏导数,对噪声很敏感,在提取边缘时往往会出现伪边缘响应。为克服拉普拉斯算子的不足,宜先对数字影像进行低通滤波，抑制噪声。高斯函数是一种很好的归一化低通滤波器,可用于对数字影像进行低通滤波以减少噪声的影响，在此基础上再利用拉普拉斯算子提取边缘,这就是高斯-拉普拉斯算子，又称为LOG(Laplacian of Gaussian)算子。为克服拉普拉斯算子的不足,宜先对数字影像进行低通滤波，抑制噪声。高斯函数是一种很好的归一化低通滤波器,可用于对数字影像进行低通滤波以减少噪声的影响，在此基础上再利用拉普拉斯算子提取边缘,这就是高斯-拉普拉斯算子，又称为LOG(Laplacian of Gaussian)算子。

(3)Canny算子
Canny算子由dst = cv.Canny( image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]] )表示
Canny算子核心优点：边缘可自动连通
算法步骤为：
平滑图像同时计算微分；
计算梯度(幅值和方向)；
梯度幅值进行非极大值抑制；
自动边缘连接

三种算子的区别：
sobel 产生的边缘有强弱，抗噪性好
laplace 对边缘敏感，可能有些是噪声的边缘，也被算进来了
canny 产生的边缘很细，可能就一个像素那么细，没有强弱之分。

3. 简述图像直方图的基本概念，及使用大津算法进行图像分割的基本原理。

灰度直方图概念
dst = cv.calcHist( images, channels, mask, histSize, ranges[, hist[, accumulate]] )
灰度直方图是关于灰度级分布的函数，是对图像中灰度级分布的统计。灰度直方图是将数字图像中的所有像素，按照灰度值的大小，统计其出现的频率。灰度直方图是灰度级的函数，它表示图像中具有某种灰度级的像素的个数，反映了图像中某种灰度出现的频率。

大津算法基本原理
retval, dst = cv.threshold( src, thresh, maxval, type[, dst] )
在对图像进行阈值分割时,所选取的分割阈值应使前景区域的平均灰度、背景区域的平均灰度与整幅图像的平均灰度之间的差异最大，这种差异用区域的方差来表示。Otsu提出了最大方差法，该算法是在判别分析最小二乘法原理的基础上推导得出的，计算过程简单，是一种常用的阈值分割的稳定算法。
该算法的详细步骤
第一步：计算灰度直方图的零阶累计矩(累加直方图)
第二步：计算灰度直方图的一阶累积矩
第三步：计算图像总体的灰度平均值
第四步：计算每一个灰度级作为阈值时，前景区域的平均灰度、背景区域的平均灰度与整幅图像的平均灰度的方差
第五步：找到最大值，然后Otsu自动选取阈值

4. 简述Harris算子对角点的定义，进行角点检测的基本原理，并说明引入角点响应函数的意义。

在进行特征提取时,我们不仅需要考虑包含角点和边缘的区域分类，而且还需要含有判断角点和边缘质量的测度或响应,响应函数值的大小可用于挑选孤立的角点像素或细化边缘像素。Harris等提出的对Moravec算子的改进，就是具有旋转不变性的角点响应测度(即角点响应算子)。Harris等提出的对Moravec算子的改进，就是具有旋转不变性的角点响应测度(即角点响应算子)。如果在角点区域内的某个像素处响应值R在8个方向上达到局部最大值,则该像素被确定为角点像素。
我们可以直观的概括下角点所具有的特征：

1.轮廓之间的交点；
2.对于同一场景，即使视角发生变化，通常具备稳定性质的特征；
3.该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化；

5. 简述Hough变换的基本原理(包括参数空间变换及参数空间划分网格统计)。

一、简单介绍

Hough变换是图像处理中从图像中识别几何形状的基本方法之一。Hough变换的基本原理在于利用点与线的对偶性，将原始图像空间的给定的曲线通过曲线表达形式变为参数空间的一个点。这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。也即把检测整体特性转化为检测局部特性。比如直线、椭圆、圆、弧线等。

二、Hough变换的基本思想

设已知一黑白图像上画了一条直线，要求出这条直线所在的位置。我们知道，直线的方程可以用y=kx+b 来表示，其中k和b是参数，分别是斜率和截距。过某一点(x0,y0)的所有直线的参数都会满足方程y0=kx0+b。即点(x0,y0)确定了一族直线。方程y0=kx0+b在参数k–b平面上是一条直线，(你也可以是方程b=-x0*k+y0对应的直线)。这样，图像x–y平面上的一个前景像素点就对应到参数平面上的一条直线。我们举个例子说明解决前面那个问题的原理。设图像上的直线是y=x, 我们先取上面的三个点：A(0,0), B(1,1), C(22)。可以求出，过A点的直线的参数要满足方程b=0, 过B点的直线的参数要满足方程1=k+b, 过C点的直线的参数要满足方程2=2k+b, 这三个方程就对应着参数平面上的三条直线，而这三条直线会相交于一点(k=1,b=0)。　同理，原图像上直线y=x上的其它点(如(3,3),(4,4)等)　对应参数平面上的直线也会通过点(k=1,b=0)。这个性质就为我们解决问题提供了方法，就是把图像平面上的点对应到参数平面上的线，最后通过统计特性来解决问题。假如图像平面上有两条直线，那么最终在参数平面上就会看到两个峰值点，依此类推。

简而言之，Hough变换思想为：在原始图像坐标系下的一个点对应了参数坐标系中的一条直线，同样参数坐标系的一条直线对应了原始坐标系下的一个点，然后，原始坐标系下呈现直线的所有点，它们的斜率和截距是相同的，所以它们在参数坐标系下对应于同一个点。这样在将原始坐标系下的各个点投影到参数坐标系下之后，看参数坐标系下有没有聚集点，这样的聚集点就对应了原始坐标系下的直线。

在实际应用中，y=kx+b形式的直线方程没有办法表示x=c形式的直线(这时候，直线的斜率为无穷大)。所以实际应用中，是采用参数方程p=xcos(theta)+y*sin(theta)。这样，图像平面上的一个点就对应到参数p—theta平面上的一条曲线上，其它的还是一样。

三、Hough变换推广

1、已知半径的圆

其实Hough变换可以检测任意的已知表达形式的曲线，关键是看其参数空间的选择，参数空间的选择可以根据它的表达形式而定。比如圆的表达形式为 ，所以当检测某一半径的圆的时候，可以选择与原图像空间同样的空间作为参数空间。那么圆图像空间中的一个圆对应了参数空间中的一个点，参数空间中的一个点对应了图像空间中的一个圆，圆图像空间中在同一个圆上的点，它们的参数相同即a，b相同，那么它们在参数空间中的对应的圆就会过同一个点（a，b），所以，将原图像空间中的所有点变换到参数空间后，根据参数空间中点的聚集程度就可以判断出图像空间中有没有近似于圆的图形。如果有的话，这个参数就是圆的参数。

2、未知半径的圆

对于圆的半径未知的情况下，可以看作是有三个参数的圆的检测，中心和半径。这个时候原理仍然相同，只是参数空间的维数升高，计算量增大。图像空间中的任意一个点都对应了参数空间中的一簇圆曲线。 ，其实是一个圆锥型。参数空间中的任意一个点对应了图像空间中的一个圆。

3、椭圆

椭圆有5个自由参数，所以它的参数空间是5维的，因此他的计算量非常大，所以提出了许多的改进算法。

四、总结

图像空间中的在同一个圆，直线，椭圆上的点，每一个点都对应了参数空间中的一个图形，在图像空间中这些点都满足它们的方程这一个条件，所以这些点，每个投影后得到的图像都会经过这个参数空间中的点。也就是在参数空间中它们会相交于一点。所以，当参数空间中的这个相交点的越大的话，那么说明元图像空间中满足这个参数的图形越饱满。越象我们要检测的东西。

Hough变换能够查找任意的曲线，只要你给定它的方程。Hough变换在检验已知形状的目标方面具有受曲线间断影响小和不受图形旋转的影响的优点，即使目标有稍许缺损或污染也能被正确识别。

6. 简述SIFT原理(重点是尺度空间和方向直方图原理)及ORB算子原理(重点是FAST和BRIEF)。

SIFT原理
1.尺度空间：
(1)人眼可自动调节尺度，完成对物体的检测和识别
(2)模仿人的视觉认知，把物体不同尺度下的图像都提供给机器，让机器能够对物体在不同的尺
度下综合信息识别
(3)因此，首先需要建立尺度空间
(4)通过高斯函数与原图像卷积，并经过下采样，可建立原始图像的尺度空间模型
2.尺度空间理论：
(1)在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺
度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作
为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取等。
(2)尺度空间方法将传统的单尺度图像信息处理技术纳入尺度不断变化的动态分析框架中
，更容易获取图像的本质特征。尺度空间中各尺度图像的模糊程度逐渐变大，能够模
拟人在距离目标由近到远时目标在视网膜上的形成过程。

3.方向直方图：
方向直方图的生成：
(1)直方图统计半径为3×1.5σ。即计算以关键点为中心半径3×1.5σ邻域内所有点的梯度方向。
(2)梯度直方图将0~360度的方向范围分为36个柱。累计落到每个方向内的关键点个数加权值，以此生成梯
度方向直方图。
(3)将梯度方向直方图中纵坐标最大的项代表的方向分配给当前关键点作为主方向，若在梯度直方图中存在一个相当于主峰值80%能量的峰值，则将这个方向认为是关键点的辅方向。辅方向的设计可以增强匹配的鲁棒性，Lowe指出，大概有15%的关键点具有辅方向，而恰恰是这15%的关键点对稳定匹配起到关键作用。
(4)对于每一个关键点，拥有三个信息：位置、尺度以及方向。接下来就是为每个关键点建立一个描述符，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照变化、视角变化等等。这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。
(5)SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示。通过对关键点周围图像区域分块，计算块内
梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象，具有唯一性。
(6)Lowe实验表明描述子采用在关键点尺度空间内44的窗口中计算的8个方向的梯度信息，共448=128维向量表征，综合效果最优。
(7) 下图是一个SIFT描述子实例。其中描述子由228维向量表征，也就是22个8方向直方图组成。左图的种子点由88单元组成。每一个小方格都代表了特征点邻域所在的尺度空间的一个像素，箭头方向代表了像素梯度方向，箭头长度代表了该像素的幅值。然后在44窗口内计算8个方向的梯度直方图，绘制每个梯度方向的累加可形成一个种子点。一个特征点由4个种子点的信息所组成。

ORB算子原理

1.oFAST特征提取

粗提取:
(1)判断特征点：从图像中选取一点P，以P为圆心画一个半径为3像素的圆。圆周上如果有连续N个像素点的灰度值比P点的灰度值大或小，则认为P为特征点。这就是大家经常说的FAST-N。有FAST-9、
FAST-10、FAST-11、FAST-12，大家使用比较多的是FAST-9和FAST-12。
(2)快速算法：为了加快特征点的提取，快速排出非特征点，首先检测1、5、9、13位置上的灰度值，如果P是特征点，那么这四个位置上有3个或3个以上的的像素值都大于或者小于P点的灰度值。如果不满足，则直接排出此点。

筛选最优特征点
机器学习的方法筛选最优特征点。简单来说就是使用ID3算法训练一个决策树，将特征点圆周上的16个像
素输入决策树中，以此来筛选出最优的FAST特征点。具体步骤如下：
(1)选取进行角点提取的应用场景下的一组训练图像。
(2)使用FAST角点检测算法找出训练图像上的所有角点。
(3)对于每一个角点，将其周围的16个像素存储成一个向量。对所有图像都这样做构建一个特征向。
(4)每一个角点的16像素点都属于下列三类中的一种，像素点因此被分成三个子集：Pd, Ps, Pb
(5)定义一个新的布尔变量Kp，如果是角点就设置为True，否则就设置为False。
(6)使用ID3算法来查询每一个子集。
(7)递归计算所有的子集直到它的熵为0。
被构建好的决策树用于其它图像的FAST检测。

使用非极大值抑制算法去除临近位置多个特征点
(1)计算特征点出的FAST得分值s（像素点与周围16个像素点差值的绝对值之和）
(2)以特征点p为中心的一个邻域（如3x3或5x5）内，若有多个特征点，则判断每个特征点的s值
(3)若p是邻域所有特征点中响应值最大的，则保留；否则，抑制。若邻域内只有一个特征点，则保留。

2.rBRIEF特征描述

BRIEF算法描述

(1)BRIEF算法计算出来的是一个二进制串的特征描述符。它是在一个特征点的邻域内，选
择n对像素点pi、qi（i=1,2,…,n）。
(2)比较每个点对的灰度值的大小，如果I(pi)> I(qi)，则生成二进制串中的1，否则为0。
(3)所有的点对都进行比较，则生成长度为n的二进制串。一般n取128、256或512，opencv默认为256。

为了改进BRIEF算法，首先建立300k个特征点测试集。对于测试集中的每个点，考虑其31x31邻域。在对图像进行高斯平滑之后，使用邻域中的某个点的5x5邻域灰度平均值来代替某个点的值，进而比较点对的大小。使用积分图像加快求取5x5邻域灰度平均值的速度。在31x31的邻域内共(315+1)x(31-5+1)=729个这样的子窗口，那么取点对的方法共有M=265356种，我们就要在这Ｍ种方法中选取256种取法，使这256种取法之间的相关性最小。