人工智能作业一——PyTorch安装教程

pycharm安装

基于本节实验在pycharm进行，但是pycharm的安装整体简单，在其他课程中已经安装完成，再次给出pycharm详细的安装链接，按照步骤进行安装配置即可。
程序运行成功截图：

PyTorch安装

1.查看自己的配置
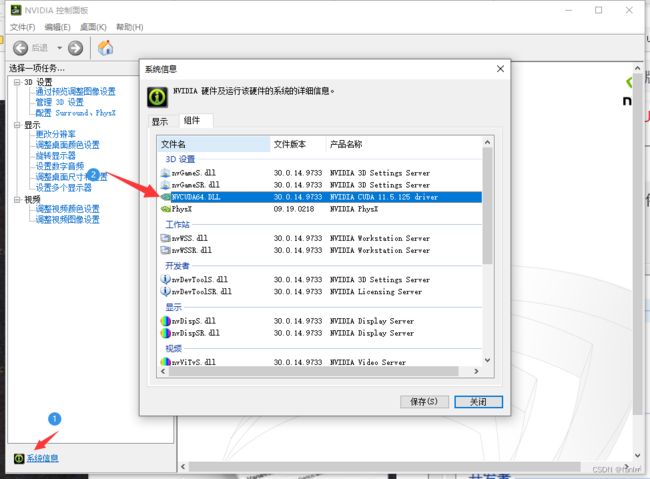
找到NVIDIA

找到自己的版本号

在PyTorch官网中选择好自己的配置，这里选择pip安装包：

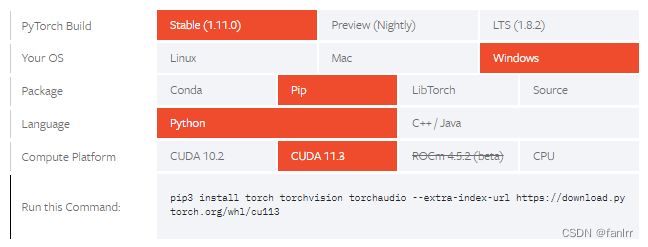
记录下Run this Command内的信息，打开cmd

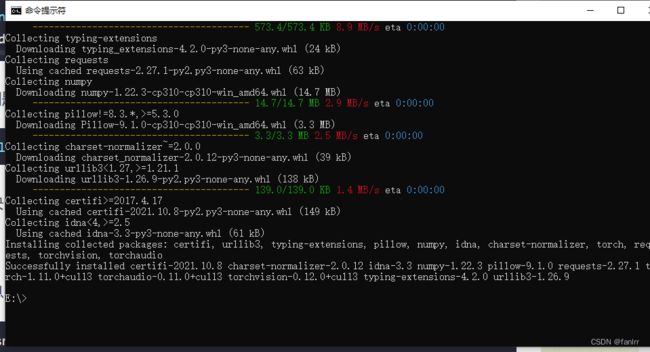
成功截图（网络不稳定可能导致安装失败，换个稳定的网络在安装一次就行）

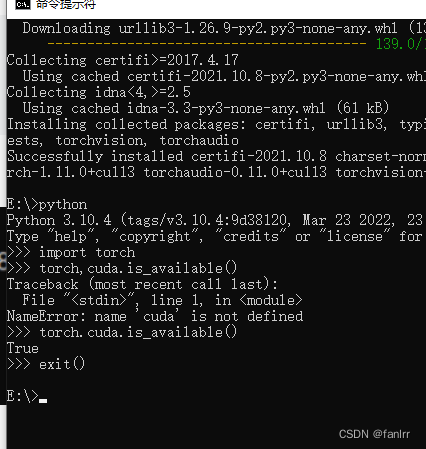
检验正确

问题总结

1.针对在cmd中的Run this Command报错分析

ERROR: Could not find a version that satisfies the requirement netsm (from versions: none)
ERROR: No matching distribution found for netsm

报错原因有两个

错误：找不到满足 netsm 要求的版本（来自版本：无）
错误：找不到与 netsm 匹配的发行版

①针对上文的配置只限于对python3.7及其以上版本可以使用，所以需要修改电脑的python配置以及pycharm的解释器版本下载地址，新版即可

然后进行安装，安装步骤直接next就好
然后配置pycharm

如下图，找到你的python地址即可

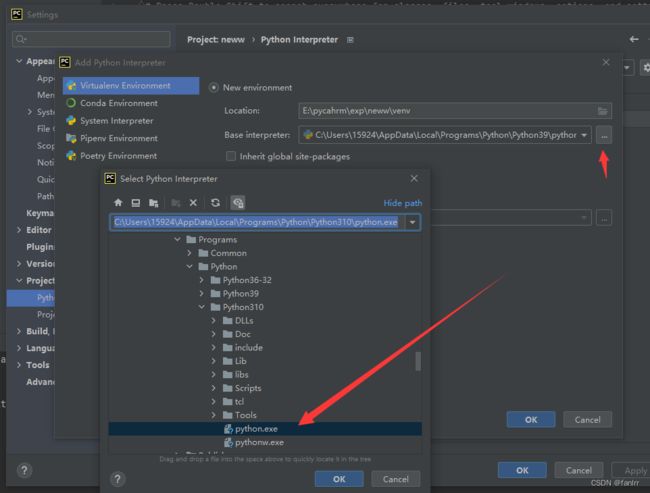
python地址查找在cmd，直接复制路径就行

2.针对pycharm的运行报错
①此种情况多为第一次使用，pycharm加载时间不足导致，稍等片刻就好
②当你删除python解释器，或者未配置解释器情况，解决办法参照问题1.配置解释器

使用PyTroch实现反向传播

训练的目的，是为了让损失更小，即在训练过程中不断更新ω的值，以使得loss最小。

所以我们在梯度下降的过程中，就是观察，并使其取向最小的趋势训练。

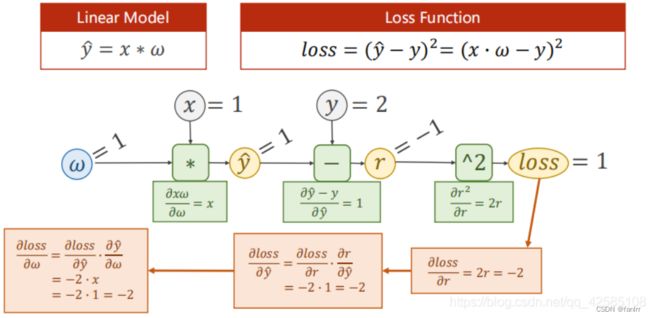
我们可以得到一般简单的线性更新计算的解析式为：

Update为：

其中，α称为学习率。（采用贪心策略）

对应的Loss Function：

但是对于我们常用的复杂的网络时，如果还是按照上述的求解ω方法，则我们需要花费大量的时间来求解相应网络连接中的权重ω，因此，我们考虑用反向传播（back promption），以求解图的方式来求解对应的权重ω。

代码来源

import torch
import matplotlib.pyplot as plt
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w = torch.Tensor([3.0])  #初始化权重
w.requires_grad = True    #说明w需要计算梯度

# 注意其中w是tensor，在实际运算中开始进行数乘。
def forward(x):
    return w*x

# 损失函数的求解，构建计算图，并不是乘法或者乘方运算
def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

print("Predict before training",4,forward(4).item())  ## 打印学习之前的值，.item表示输出张量的值

learning_rate = 0.01
epoch_list = []
loss_list =[]
#训练
for epoch in range(100):
    for x,y in zip(x_data,y_data):
        l=loss(x,y)
        l.backward()        #向后传播
        print('\tgrad',x,y,w.grad.item())    # 将梯度存到w之中,随后释放计算图,w.grad.item()：取出数值
        w.data = w.data - learning_rate*w.grad.data # 张量中的grad也是张量,所以取张量中的data,不去建立计算图
        w.grad.data.zero_()  # 释放data
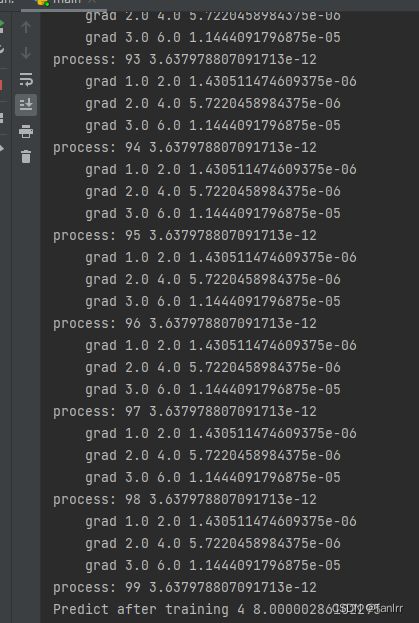
    print("process:",epoch,l.item())
    epoch_list.append(epoch)
    loss_list.append(l.item())
    
print('Predict after training', 4, forward(4).item())

#绘制可视化
plt.plot(epoch_list,loss_list)
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.show()

结果为：

可以看出随着迭代次数的增加，损失函数会越来越小

参考资料

ERROR: Could not find a version that satisfies the requirement xxx (from versions: none)
Pytorch深度学习（三）：反向传播