手写数字识别实践（二）：基于线性SVM与PyQt5

  就知道贝叶斯只是一个开始了…这次老师要求使用线性分类器，可以直接在（一）的设计基础上进行功能拓展（其实就是把线性分类器做出来再往朴素贝叶斯分类器的位置一塞而已）。
  Emmm…原本是想和（一）一样学习完原理和算法以后自己亲自把分类器 COPY 手撸出来的，结果在网上找相关资料的时候一眼望去全是用包的，要么是 sklearn 要么是 cv 。好不容易找到一个贴出手撸SVM的神仙博客，然后一套操作下来直接给我看懵了QAQ（挖坑挖坑，指不定以后开窍了就能参照教科书式的写法把线性SVM撸出来：Python实现基于SVM算法的手写数字识别系统）。现在果然还是得老老实实用包吧，又菜又没时间，撸内核对咱来说还是太强人所难了点 >…<
  编程及运行环境： VS Code + Win10（Ubuntu也是可以跑的）
  使用软件包： PIL + PyQt5 + numpy + pandas + matplotlib + sklearn

一、理论基础

  如果目的只在应用SVM，理论基础只需阅读第1节的内容即可满足需求。

1.线性可分、近似线性可分与线性不可分

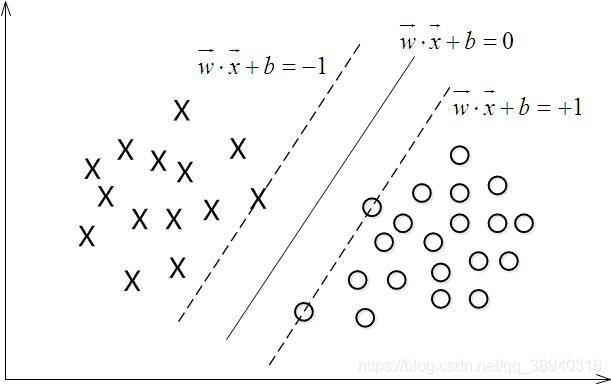
  支持向量机(Support Vector Machine,SVM)是一种二类分类模型，其基本模型是定义在特征空间上的间隔最大（不同于感知器的误分类最小）的线性分类器。而一个线性分类器的学习目标就是要在 n 维的数据空间中找到一个超平面来界定不同类别。超平面方程可以表示为
$$w^{T}x+b=0$$   对于分类函数 $f(x)=w^{T}x+b$，当 $f(x)=0$ 时 $x$ 即为超平面上的点， $f(x)>0、f(x)<0$ 就分别对应类别 $y=1、y-1$ 的数据点，如下图所示：

  分类的正确性可以通过观察 $w^{T}x+b、y$ 的符号是否一致来进行判断，于是引入了函数间隔 $\widehat{{\gamma }_i}$ 的概念。对于任意的输入样本点 $(x_i,y_i)$：
$$\widehat{{\gamma }_i}=y_i(w^T{x}_i+b)=y_{i}f(x_i)$$   而超平面 $(w,b)$ 关于数据集T中的所有样本点 $(x_i,y_i)$ 的函数最小间隔值即为超平面 $(w,b)$ 关于数据集T的函数间隔 ：
$$\hat{\gamma }=min\widehat{{\gamma }_i},i=1,2,...n$$   从函数间隔的公式特性可以看出，如果把 $w$ 和 $b$ 成比例改变，那么 $\hat{\gamma }$ 也会相应地改变，然而超平面还是那个超平面。因此为了能真正得到样本点到超平面的距离，需要将引入新的计量方式：

$${\gamma }_i=\frac{\widehat{{\gamma }_i}}{||w||}（||w||=\sqrt{w^{T}w}）$$ $$\gamma =min{\gamma }_i,i=1,2,...n$$  这就是几何间隔 $\gamma$。前面提到的间隔最大，指的就是几何间隔最大，所以最大间隔分类器的目标函数可以定义为：
$$\underset{w,b}{\max }\frac{2\hat{\gamma }}{||w||}，s.t{y}_i(w^T{x}_i+b)=\widehat{{\gamma }_i}\ge \hat{\gamma }，i=1,2,...,n$$   如果简化一下，令函数间隔 $\hat{\gamma }=1$（为什么取1），就有：
$$\underset{w,b}{\max }\frac{2}{||w||}，s.t{y}_i(w^T{x}_i+b)\ge 1，i=1,2,...,n$$   众所周知 $max$ 问题是可以转换成 $min$ 问题的，即：
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2，s.t{y}_i(w^T{x}_i+b)\ge 1，i=1,2,...,n$$   解得最优的 $w^{\ast }、b^{\ast }$ 即得到分类超平面，进而得到分类决策函数（至于怎么解的，总之就是很懵逼，约束最优化这块真的是白板QAQ）。在上式中，对于满足 $y(w^{T}x+b)=1$ 或者 $y(w^{T}x+b)=-1$ 的 $x$ 也被称为支持向量，其对应的几何意义见下图：

PS:在决定分类超平面时只有支持向量起作用，而其他实例点并不起作用。如果移动支持向量将改变所求的解；但是如果在间隔边界以外移动其他实例点，甚至去掉这些点，解并不会改变。

  现在换一个角度，有线性可分的样本集，自然也就有线性不可分的样本集。但是实际上两者之间并没有到“有你没我”的程度，从模糊数学上看，在“几乎”线性不可分之前，还会有一种“基本上”线性可分的情况（就像是在做实验验证物理规律的时候很有可能会出现那么一两个点的位置偏离了大部分数据点的变化趋向），也就是近似线性可分。
  在近似线性可分情况下的处理方式与线性可分思路大体相同，只要给函数间隔加上一个松弛变量 $\xi$ , 把那些过于离谱的点忽略掉就好了，这就是间隔最大化的软化。反映到公式上其实就是
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i，s.t\{\begin{array}{l}{y}_i(w^T{x}_i+b)\ge 1-{\xi }_i，i=1,2,...,n\\ {\xi }_i\ge 0,i=1,2,...,N\end{array}$$   这里的 $C>0$ 就叫惩罚参数，对应下文参数说明部分的 $C$ 。然后就是线性可分那一通操作啦。
  而对于线性不可分的数据集，SVM的处理方法是选择一个核函数Kernel，通过将数据映射到高维空间后，在高维空间使用线性分类器来解决在原始空间中线性不可分的问题（如下图）。

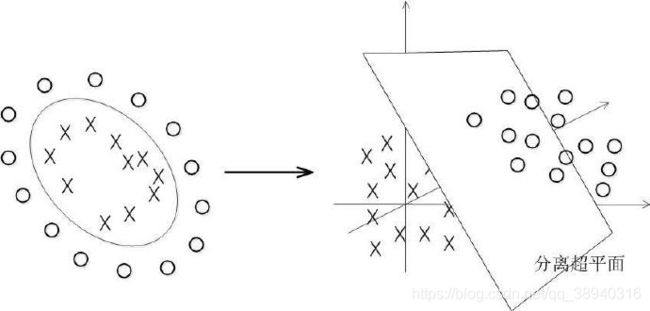
  核函数简单来说就是用来在原来的低维空间提前完成原本需要映射到高维空间的计算（在求解 $w$ 的过程中会发现就是内积运算）的一种简便方法。

PS:实际上在之前的线性可分和近似线性可分的问题中，最后一部分的约束最优化求解过程没底子硬是把咱给看懵了所以没有写出来（挖个坑，毕竟也是挺核心的内容，如果期末考核老师有刚需那还得回来填坑），此外很明确的一点就是最终的决策函数中只包含待分类样本和训练样本中的支持向量的内积运算。

2.复习阶段追加——线性可分的约束最优化

  回来填坑！！
  在第1节中线性可分的情况中，最后是把问题转化为了下面的约束最优化问题
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2，s.t{y}_i(w^T{x}_i+b)\ge 1，i=1,2,...,n$$   给每条约束条件加上一个拉格朗日乘子 ${\alpha }_i\ge 0$，定义拉格朗日函数：
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^n{\alpha }_i(1-y_i(w^T{x}_i+b))$$   其中 $\alpha =({\alpha }_1,{\alpha }_2,...,{\alpha }_n)$。

PS:不知拉格朗日乘子为何物可参考：如何理解拉格朗日乘子法。这么干的目的也就是为了把约束条件融合到目标函数里，使之配成与变量数量相等的等式方程，从而求出原函数极值的各个变量的解。

  很明显 $L(w,b,\alpha )$ 的极值点处的 $w、b$ 就是最优的 $w^{\ast }、b^{\ast }$。 令 $L(w,b,\alpha )$ 对 $w、b$ 的偏导为0可得
$$w=\sum _{i=1}^n{\alpha }_i{y}_i{x}_i$$ $$0=\sum _{i=1}^n{\alpha }_i{y}_i$$   代入 $L(w,b,\alpha )$ 中消去 $w、b$，同时考虑到 $L(w,b,\alpha )$ 取得极值时，$\alpha$ 应该取得最大值，所以现在问题变成了
$$\underset{\alpha }{\max }\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j，s.t\{\begin{array}{l}{\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ {\alpha }_i\ge 0\end{array}$$   到了这里就可以使用SMO算法求解 $\alpha$ 了。

PS:推导过程略微复杂，咱看不懂 这里最后还是略去，只上结论。此外，严格意义上说在构造拉格朗日函数以后目标函数的真实形式应该是
$$\underset{w,b}{\min }\underset{\alpha }{\max }L(w,b,\alpha )$$ 而上面之所以能转换成
$$\underset{\alpha }{\max }\underset{w,b}{\min }L(w,b,\alpha )$$ 是因为这里满足使两者等价的 Slater 条件和 KKT 条件（具体情况在参考资料部分附有相关博文链接）。正是由于 KKT 条件，所以对于任意的训练样本 $(x_i,y_i)$，总有 ${\alpha }_i=0$ 或 $y_i(w^T{x}_i+b)=1$。如果是 ${\alpha }_i=0$，则该样本就根本不会给 $f(x)=w^{T}x+b=({\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i{)}^{T}x+b$ 带来任何影响。这也是最终模型（决策函数）仅和支持向量有关的原因。

  SMO的基本思路是先固定 ${\alpha }_i$ 之外的所有参数，然后求 ${\alpha }_i$ 上的极值。由于存在约束 ${\sum }_{i=1}^n{\alpha }_i{y}_i=0$ ,如果固定除 ${\alpha }_i$ 之外的其他变量，则 ${\alpha }_i$ 就可由其他变量导出。这样，SMO 就可以每次选择两个变量 ${\alpha }_i、{\alpha }_j$，并固定其他参数。
  SMO的主要步骤可以总结为两步：
  （1）启发式选取一堆需要更新的变量 ${\alpha }_i、{\alpha }_j$（两变量对应的样本之间的间隔最大）；
  （2）固定 ${\alpha }_i、{\alpha }_j$ 以外的参数，求解 ${\alpha }_i、{\alpha }_j$。
  详细的推导和求解过程就不深究了（再往下挖人都要给挖没了QAQ）。

3.特征提取与主成分分析（PCA）

  前两节算是 SVM 的正统理论，这一节则是单纯的彩头。在前一篇实现朴素贝叶斯分类器的博客中简单提及了直接使用原始特征带来的局限性，反正都要使用sklearn包构建SVM了不如也顺便用下里面的PCA 因此利用这一次机会正式处理一下（当然并没有做数字边界抓取）。
  主成分分析（principal Component Analysis，PCA）是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量。从矩阵论的角度来看，PCA降维的基本思想就是：选择不同的基可以对同样一组数据给出不同的表示，如果基的数量少于向量本身的维数，则可以达到降维的效果 。
  那么如何选出最优的基呢？一种直观的看法是：希望投影后的投影值尽可能分散，因为如果重叠就会有样本消失。同时，为了让两个变量尽可能表示更多的原始信息，我们希望它们之间不存在线性相关性，因为相关性意味着两个变量不是完全独立，必然存在重复表示的信息。于是乎就得到了PCA的优化目标：将一组 M 维向量降为 d 维，其目标是选择 d 个单位正交基，使得原始数据变换到这组基上后，各变量两两间协方差为 0，而变量方差则尽可能大（在正交的约束下，取最大的 d 个方差）。
  具体的数学证明可以参阅参考资料中的相关文章，这里就不再贴出，仅附算法步骤说明：

• 对样本集 $X$ 中的所有样本进行零均值化，$x_i=x_i-\frac{1}{m}{\sum }_{i=1}^m{x}_{im}$
• 求样本集 $X$ 的协方差矩阵 $C=\frac{1}{m}X{X}^T$
• 求 $C$ 的特征值，选取前 $d$ 个较大的特征值（$d$ 为要将 $X$ 变换到的维数）
• 计算这 $d$ 个特征值的特征向量 $u_j$，归一化后构成变换矩阵 $U=[u_1,u_2,...,u_d]$
• 计算得到 $d$ 维向量 $X^{\ast }=U^{T}X$，这就是替代 $X$ 进行分类的新的模式向量

PS：既然是做数据提取，信息丢失就一定会存在。不过可以在选择前 $d$ 个特征向量时，使 ${\sum }_{i=0}^{d-1}{\lambda }_i/{\sum }_{i=0}^{N-1}{\lambda }_i\ge \alpha =0.99$，这样就能保持原样本99%的信息。

二、程序设计实践

1.流程图与数据预处理

  直接使用博文手写数字识别实践（一）：基于朴素贝叶斯分类器与PyQt5中的设计思路与数据的二值化处理结果。

2.sklearn.svm包的调用（含PCA）

  只是简单地用一用的话，全部代码加起来不会超过20行的样子吧……当然加上模型性能指标测试的话得另说。另外关于LinearSVC()和SVC(kernel=‘linear’)，这两种写法是博主在网上找其他人的sklearn包用法时发现的（貌似还有个NuSVC，不过既然没有用到自然就没管了），看上去似乎干的是同一件事，但是一般来说，一个函数就可以完成的事为什么还要再加一个功能上完全重复的函数，所以这两者必然在什么地方有所不同。在网上搜录了一下相关的区别说明：

• LinearSVC() 最小化 hinge loss的平方，
  SVC(kernel=‘linear’) 最小化 hinge loss；
• LinearSVC() 使用 one-vs-rest 处理多类问题，（训练N个分类器）
  SVC(kernel=‘linear’) 使用 one-vs-one 处理多类问题；（训练N(N-1)/2个分类器，因此会更慢一些）
• LinearSVC() 使用liblinear执行，
  SVC(kernel=‘linear’)使用libsvm执行；
• LinearSVC() 可以选择正则项和损失函数，
  SVC(kernel=‘linear’)使用默认设置。

  一句话：在解决线性可分问题上，LinearSVC()是专业的 。只要确定了需要进行分类的数据集线性可分，大可以放心使用LinearSVC()。
  关于PCA：API使用起来极其方便，第一个参数 n_components 指定要降到的维数，第二个参数 copy 指定是在给定数据集上降维训练还是在给定数据集的副本上降维训练（明眼人都能看出来这两个选项是怎么对应的吧）。fit_transform 函数使用给定的数据集训练PCA模型并返回降维后的数据。在获得PCA模型后需要再次使用时调用transform函数就可以了。
  关于ROC曲线：存疑。虽然用的全是库函数，但是结果自觉过于离谱。原因未查明，对此持保留态度。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.calibration import CalibratedClassifierCV
from sklearn.decomposition import PCA
from sklearn.metrics import roc_curve, auc
np.set_printoptions(suppress=True)

def create_svm(trainset, train_labels):
    # 获取一个支持向量机模型
    clf = CalibratedClassifierCV(svm.LinearSVC(dual=False))

    # 使用PCA降维
    pca = PCA(n_components=25,copy=True)
    new_trainset = pca.fit_transform(trainset)

    # 把数据丢进去
    clf.fit(new_trainset, train_labels)

    return clf, pca

def Test_Predict(testset, test_labels, clf, pca):
    accuracy = []
    pre_right = np.zeros(10)                    # 每一类预测正确的数量
    act_numbers = np.zeros(10)                  # 每一类的样本实际数量（P）   
    fpr = dict()
    tpr = dict()
    roc_auc = dict()

    new_testset = pca.transform(testset)

    result = clf.predict(new_testset)
    y_score = clf.predict_proba(new_testset)

    # 统计测试数据中各类数字的数量
    for i in test_labels:
        act_numbers[i] += 1

    for count in range(len(test_labels)):
        if result[count] == test_labels[count]:
            pre_right[result[count]] += 1
        if (count+1) % 500 == 0:
            accuracy.append(float(pre_right.sum())/(count+1))            # 计算总体预测准确率

    print(pre_right)
    print('-------------------------------------------------------------------')
    print(act_numbers)
    print('-------------------------------------------------------------------')
    print(pre_right/act_numbers)

    plt.figure()
    plt.plot(np.arange(1,21),accuracy,marker="o",markersize=8)
    plt.xlabel("x -- 1:500")
    plt.title("Predict Accuracy Rate")
    plt.show()

    plt.figure()
    for i, color in zip(range(10),['red','orange','gold','green','cyan','blue','purple','peru','brown','black']):
        fpr[i], tpr[i], _ = roc_curve(test_labels, y_score[:,i], pos_label=i)
        roc_auc[i] = auc(fpr[i], tpr[i])
        plt.plot(fpr[i], tpr[i],color=color,lw=2,label='Class {0} (area = {1:0.2f})'
        ''.format(i, roc_auc[i]))
    plt.plot([0, 1], [0, 1], 'k--', lw=2)
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('ROC Curve')
    plt.legend(loc="lower right")
    plt.show()

    return accuracy, result

def Predict(testset, clf, pca):
    new_testset = pca.transform(testset)

    return clf.predict(new_testset)

3.sklearn.svm LinearSVC及SVC的参数说明

  讲道理用了包还懒得调参确实有点令人发指，但是其他方面的事情堆得挺多的实在不想把时间花在调参上面QAQ…保险起见就算不调参还是附一下这两个函数的参数说明吧，保不准以后又会有刚性需求。
（1）LinearSVC参数说明（实时更新的源英文说明文档）

'''
sklearn.svm.LinearSVC(penalty='l2', loss='squared_hinge', dual=True, tol=0.0001, C=1.0, multi_class='ovr', 
fit_intercept=True, intercept_scaling=1, class_weight=None, verbose=0, random_state=None, max_iter=1000)

penalty：{‘l1’, ‘l2’}, default=’l2’
正则化参数，有L1和L2两种参数可选，SVC函数中使用的相关参数为L2(未提供选择参数接口)，LinearSVC独有
loss：{‘hinge’, ‘squared_hinge’}, default=’squared_hinge’
损失函数，有‘hinge’和‘squared_hinge’两种可选，前者称为L1损失，后者称为L2损失，其中hinge是SVM的标准损失，squared_hinge是hinge的平方
dual：bool, default=True
是否转化为对偶问题求解，在样本数大于特征维度时可将其设置为False
tol：float, default=1e-4
残差收敛条件，默认是0.0001
C：float, default=1.0
惩罚系数，越大代表这个分类器对在边界内的噪声点的容忍度越小，分类准确率高，但是容易过拟合，泛化能力差。所以一般情况下，应该适当减小C，对在边界范围内的噪声有一定容忍
multi_class：{‘ovr’, ‘crammer_singer’}, default=’ovr’
负责多分类问题中分类策略制定，有‘ovr’和‘crammer_singer’ 两种参数值可选。'ovr'的分类原则是将待分类中的某一类当作正类，其他全部归为负类，通过这样求取得到每个类别
作为正类时的正确率，取正确率最高的那个类别为正类；‘crammer_singer’ 是直接针对目标函数设置多个参数值，最后进行优化，得到不同类别的参数值大小
fit_intercept：bool, default=True
是否计算截距
intercept_scaling：float, default=1
当fit_intercept为真时，给实例向量X附加一个定值为intercept_scaling的“合成”特征，使其变为[x,intercept_scaling]，此时截距也会变成intercept_scaling *合成特征
权重。如果要减小正则化对“合成”特征全终的影响，就需要增加intercept_scaling的值
class_weight：dict or ‘balanced’, default=None
用来处理不平衡样本数据，可以直接以字典的形式指定不同类别的权重，也可以使用balanced参数值
verbose：int, default=0
启用详细输出，可能无法在多线程上下文中正常工作
random_state：int or RandomState instance, default=None
随机种子
max_iter：int, default=1000
最大迭代次数
'''

 （2）SVC参数说明（实时更新的源英文说明文档）

'''
sklearn.svm.SVC(*, C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, 
cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)

C：float, default=1.0
惩罚系数,LinearSVC同款参数
kernel：{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}, default=’rbf’
算法中采用的核函数类型，参数选择上除了以上自带的5种以外也可以自定义核函数
	0 – 线性核：u'v
	1 – 多项式核：(gamma*u'*v + coef0)^degree
	2 – 径向基核(高斯核)：exp(-gamma|u-v|^2)
	3 – 双曲正切函数tanh核：tanh(gamma*u'*v + coef0)
	4 — 核矩阵
degree：int, default=3
指定kernel为'poly'时，表示选择的多项式的最高次数；若指定kernel不是'poly'，则忽略
gamma：{‘scale’, ‘auto’} or float, default=’scale’（version 0.22之前的默认参数是’auto‘）
’rbf‘，’poly‘和’sigmoid‘的核函数系数；'scale'下gamma的值会被设置成1 / (n_features * X.var())，’auto‘下则使用1 / n_features；gamma越大，σ越小，
使得高斯分布又高又瘦，造成模型只能作用于支持向量附近，可能导致过拟合；反之，gamma越小，σ越大，高斯分布会过于平滑，在训练集上分类效果不佳，可能导致欠拟合
coef0：float, default=0.0
核函数常数值(y=kx+b中的b值)，只有‘poly’和‘sigmoid’核函数有
shrinking：bool, default=True
是否使用启发式搜索。如果能预知哪些变量对应着支持向量，则只要在这些样本上训练就够了，其他样本可不予考虑，这不影响训练结果，但降低了问题的规模并有助于迅速求解。
进一步，如果能预知哪些变量在边界上(即a=C)，则这些变量可保持不动，只对其他变量进行优化，从而使问题的规模更小，训练时间大大降低。这就是Shrinking技术。 
Shrinking技术基于这样一个事实：支持向量只占训练样本的少部分，并且大多数支持向量的拉格朗日乘子等于C
probability：bool, default=False
是否使用概率估计；必须在fit()方法前使用，该方法的使用会降低运算速度
tol:float, default=1e-3
残差收敛条件，默认是0.001，即容忍1000分类里出现一个错误；误差项达到指定值时则停止训练
cache_size:float, default=200
核函数使用的缓存大小，用来限制计算量大小，默认是200M
class_weight：dict or ‘balanced’, default=None
类别的权重，字典形式传递；设置类i的参数C为class_weight[i]*C；如果没有给出，所有类的weight为1
verbose：bool, default=False
是否启用详细输出，LinearSVC同款参数；在训练数据完成之后，会把训练的详细信息全部输出打印出来，可以看到训练了多少步，训练的目标值是多少
max_iter：int, default=-1
最大迭代次数，默认是-1，即没有限制；这个是硬限制，它的优先级要高于tol参数，不论训练的标准和精度达到要求没有，都要停止训练
decision_function_shape：{‘ovo’, ‘ovr’}, default=’ovr’
‘ovo’ 一对一，为one v one，即将类别两两之间进行划分，用二分类的方法模拟多分类的结果，决策所使用的返回的是（样本数，类别数*(类别数-1)/2）； 
‘ovr’ 一对多，为one v rest，即一个类别与其他类别进行划分，返回的是(样本数，类别数)，或者None，就是不采用任何融合策略。
’ovr‘效果要比'ovo'略好一点（因为’ovo‘划分出来的歧义区域会比'ovr'小一些），当然也更慢一点
break_ties：bool, default=False（version 0.22 新加的参数）
break_ties为’True‘时，若decision_function_shape='ovr'，类数> 2，将根据decision_function的置信值来结束预测
random_state：int or RandomState instance, default=None
随机种子

主要调节的参数有：C、kernel、degree、gamma、coef0
'''

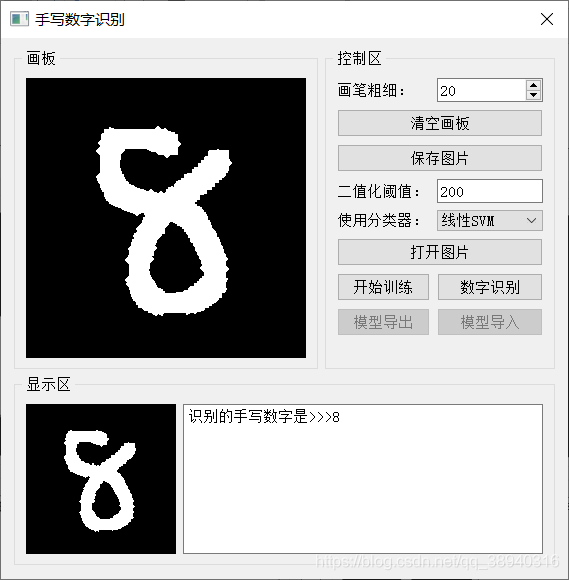
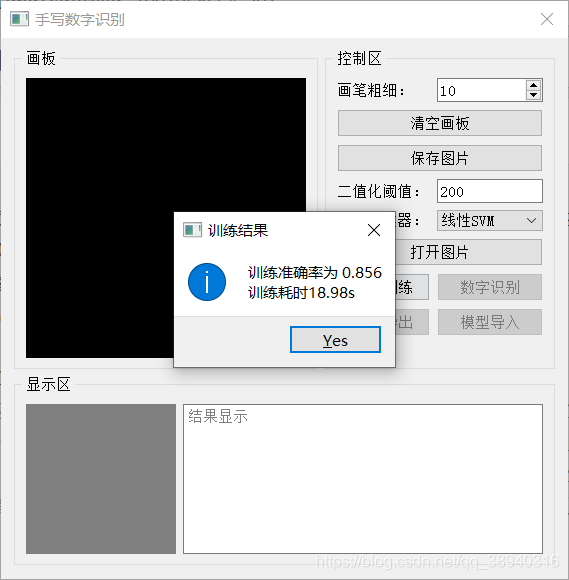
三、实际效果

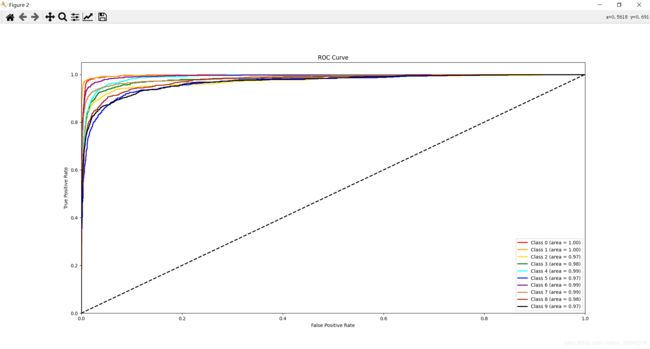
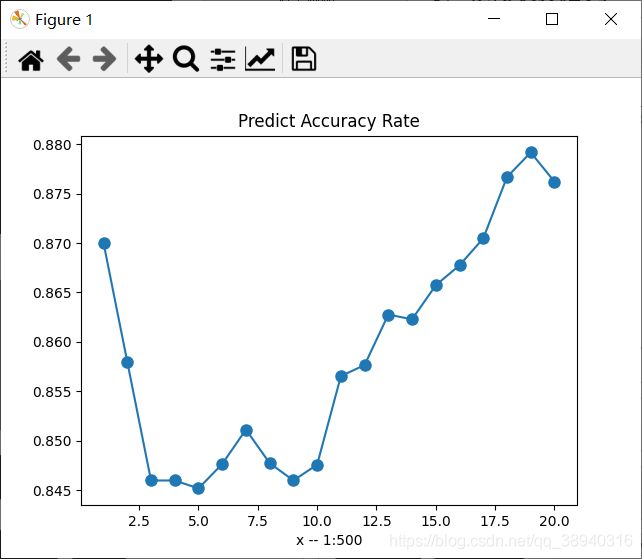
  使用MNIST 28 x 28数据集，训练数据6w，测试数据1w。第一张是使用了PCA把784维的原始特征降到25维的，第二张是直接使用原始特征的。可以看到准确率确实有一定程度的下降，不过训练耗时也小了很多：


  这里往下就都是使用PCA的测试结果了。Emmm……准确率怎么又是这个样子：


  AUC = 1都出来了，全看下来最低也是0.97……先不论ROC曲线，单看上面的各类测试准确率就感觉这个AUC 不靠谱，但是写的相关程序全是用库函数计算的，也不知道问题出在哪Orz……不管了，先贴着，以后弄明白了再回来修。

四、参考资料

• 李航 《统计学习方法》第7章
• 邱锡鹏 《神经网络与深度学习》第3章
• 周志华 《机器学习》第6章
• 支持向量机（SVM）必备知识(KKT、slater、对偶）
• GitHub:SVM
• 核函数的定义与作用 - 知乎
• SVM之Mnist手写数字识别 - 知乎
• 基于SVM技术的手写数字识别
• ⭐支持向量机通俗导论（理解SVM的三层境界）
• 【机器学习】降维——PCA(非常详细) - 知乎
• Python实现PCA降维
• ROC曲线的绘制过程/AUC/TPR、FPR、敏感度和特异度

五、复习阶段追加——ROC曲线与AUC

  想了想还是加上吧，毕竟这一次用了ROC而且最后还出现了难以置信的结果，把知识梳理一遍以后回来看的时候指不定能发现问题。
  在介绍ROC曲线之前，要先说说混淆矩阵。这个用来评估分类器性能的东西实际上是针对二分类的情况进行定义的，对它而言只有正例和反例，没有其他类别，也就是“非此即彼”（放到多分类中就相当于“一对多”了）。在只看这两大类的条件下，样本在实际上可以分成正例和反例两个部分，而分类器的预测结果也可以分成正例和反例两个部分，这样组合一下，咱就得到了四种样本，也就是混淆矩阵构成元素：

真实情况	预测结果
	正例	反例
正例	TP	FN
反例	FP	TN

  TP：被判定为正例，实际上为正例        FN：被判定为反例，实际上为正例（假阴性）
  FP：被判定为正例，实际上为反例（假阳性）  TN：被判定为反例，实际上为反例

  感觉还行？再来几个指标：

• 查准率（精确率）：判定为正例的样本中有多少是正确的 $$Precision=\frac{TP}{TP+FP}$$
• 查全率（召回率） ：所有实际上为正例的样本中有多少被找到了 $$Recall=\frac{TP}{TP+FN}$$
• 真阳性率：所有实际上为正例的样本中有多少被找到了 $$TPR=\frac{TP}{TP+FN}$$
• 假阳性率：所有实际上为反例的样本中有多少被误判为正例了 $$FPR=\frac{FP}{FP+TN}$$
• 敏感性：表示研究方法把正例样本正确识别出来的能力，高要求表现为“宁可错杀一百不可放过一个” $$S_n=\frac{TP}{TP+FN}$$
• 特异性：表示研究方法把反例样本正确识别出来的能力，高要求表现为“宁可放过一百不可错杀一个” $$S_p=\frac{TN}{FP+TN}$$

  在实际应用中应该同时保证特异性和敏感性不能太低。如果敏感性高而特异性低，就容易产生较高的假阳性率；如果敏感性低而特异性高，就容易产生较高的假阴性率。

PS：混淆矩阵为什么要叫混淆矩阵啊，当然是因为它概念多特别容易混淆啊（doge）

  接下来就是ROC曲线的绘制方法。ROC曲线的横坐标为 FPR，纵坐标为 TPR。但是经过训练和测试的模型，显然对于任意一类来说只有一组确定的 FPR 和 TPR，这怎么画一条曲线出来？这里涉及到一个阈值的设定。模型经过测试得出测试集的预测结果这一决策过程，实际上可以看成是根据一个阈值来评判某一个样本是否归于特定的类。如果使这个阈值可调，即给一组阈值依次代入分类器，对于一个测试集中的每一类就可以得到很多组 FPR 和 TPR，ROC曲线也就出来了。至于AUC，就是ROC曲线的面积，其值为0~1之间，越大越好。
  所以以识别十类手写数字为例，绘制ROC曲线的步骤可以简要概括为：

• 获取测试集样本的概率矩阵（对于每一个样本都应该有将其归到0~9这十类的10个概率，总和为1，共计1w样本，那就是10000 * 10的概率矩阵）
• 调用 ROC 曲线、AUC计算函数得到每一类的 FPR、TPR 和 AUC 的值
• 用 matplotlib 的 API 把它们画出来

  具体实现过程见上文中的代码。

PS：对于前面的ROC、AUC的异常，目前唯一想到的可能是这1w的数据集中每一类数量占比都是10%左右，这样对每一类单作分析的时候，就会出现正例：反例 = 1：9 的情况，有可能会影响到结果（实际上并不会，因为ROC曲线的特性之一就是曲线形状不会受到样本分布变化的影响，这里是死马当活马医了），然后就手动把测试集中 2 和 3 的样本单独切出来（2000个左右） 重新投入，发现并没有什么卵用，AUC还是居高不下(这只是博主的情况，也有可能是代码写错了，如果有相同的问题还是建议尝试一下)，咱是真没招了QAQ
附测试结果图：



2020年12月20日补充：突然又想到有可能是因为概率矩阵分布过于集中导致阈值划分意义不明显。比如说第一个样本是0，然后得到的概率矩阵中0的概率就占了0.9，1~9这9个概率去分剩下的0.1，这样概率差距就过于悬殊了。但是即便假设成立也没有行之有效的解决方案。