450-删除二叉搜索树中的节点
450-删除二叉搜索树中的节点
删除二叉搜索树中的节点
Category Difficulty Likes Dislikes
algorithms Medium (49.03%) 606 -
Tags
Companies
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
1.首先找到需要删除的节点;
2.如果找到了,删除它。
示例 1:
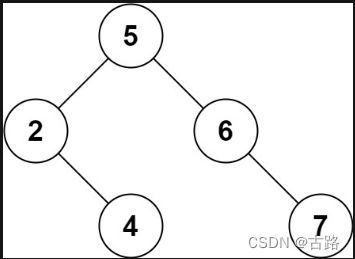
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
节点数的范围 [0, 104].
-10^5 <= Node.val <= 10^5
节点值唯一
root 是合法的二叉搜索树
-10^5 <= key <= 10^5
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
确定遍历方式: 显然应该选择前序遍历
使用待删除节点的前驱或者后继直接替换待删除节点,然后删除删除前驱或后继,对树的结构是改变最小的。
这个版本是完全将逻辑细节展示出来的版本:
// 待删除的节点为:
// case 1.叶子节点--直接删除
// case 2.只有左子树或只有右子树--子承父业
// case 3.左右子树都有--找前驱或后继进行替换(值替换,然后删除替换后的前驱或后继)
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
// 1.终止条件:没找到待删除节点
if (root == nullptr) return root;
// 2.前序遍历
// 中 : 找到待删除的节点
if (key == root->val) {
// case 1
if (root->left == nullptr && root->right == nullptr) return nullptr;
// case 2
else if (root->left == nullptr) return root->right;
else if (root->right == nullptr) return root->left;
else {// case 3
// 找后继
TreeNode* successor = root->right; // 右拐一次
TreeNode* parent = root; // 记录后继的父节点用于删除替换后的“后继”
while (successor->left) { // 然后使劲左拐
parent = successor;
successor = successor->left;
}
// 交换值
swap(root->val, successor->val);
// 删除交换后的“后继”
// 此时的root值是successor的值,根据此来计算其来自于parent哪个分支,从而删除后继节点
if (root->val == parent->val) { // case 3.1这种情况是root就是parent,交换值前后都满足相等
parent->right = successor->right;
} else if (root->val < parent->val) { // case 3.2
parent->left = successor->right;
} else if (root->val > parent->val) {
parent->right = successor->right;
}
return root;
}
}
if (key < root->val) { // 左
root->left = deleteNode(root->left, key);
return root;
}
if (key > root->val) { // 右
root->right = deleteNode(root->right, key);
return root;
}
return nullptr;
}
};
整理一下:
// 待删除的节点为:
// case 1.叶子节点--直接删除
// case 2.只有左子树或只有右子树--子承父业
// case 3.左右子树都有--找前驱或后继进行替换(值替换,然后删除替换后的前驱或后继)
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
// 1.终止条件:没找到待删除节点
if (root == nullptr) return root;
// 2.前序遍历
if (key == root->val) { // 中
// case 1 + 2
if (root->left == nullptr) return root->right;
else if (root->right == nullptr) return root->left;
else {// case 3
// 找后继
TreeNode* successor = root->right; // 右拐一次
TreeNode* parent = root; // 记录后继的父节点用于删除替换后的“后继”
while (successor->left) { // 然后使劲左拐
parent = successor;
successor = successor->left;
}
// 替换值
root->val = successor->val;
// 删除交换后的“后继”
if (successor->val < parent->val)
parent->left = successor->right;
else
parent->right = successor->right;
}
return root;
}
if (key < root->val) root->left = deleteNode(root->left, key); // 左
if (key > root->val) root->right = deleteNode(root->right, key); // 右
return root;
}
};
更进阶的简化,在交换root值与后继节点值后,相当于把待删除节点往后移动了,而且此时case3就转变成了case1或2,可以直接继续遍历删除,但此时就不能返回root,需要把整棵树遍历完。
// 待删除的节点为:
// case 1.叶子节点--直接删除
// case 2.只有左子树(case 2.1)或只有右子树(case 2.2)--子承父业
// case 3.左右子树都有--找前驱或后继进行替换(值替换,然后删除替换后的前驱或后继)
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return root;
if (root->val == key) {
// case 1 + case 2.1
if (root->right == nullptr) {
return root->left;
}
// case 2.2 + case 3
TreeNode* successor = root->right;
while (successor->left) {
successor = successor->left;
}
// 把 key 往后移,将 case 3 转为 case 1 或case 2
swap(root->val, successor->val);
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
找前驱的版本:
// 待删除的节点为:
// case 1.叶子节点--直接删除
// case 2.只有左子树(case 2.1)或只有右子树(case 2.2)--子承父业
// case 3.左右子树都有--找前驱或后继进行替换(值替换,然后删除替换后的前驱或后继)
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return root;
if (root->val == key) {
// case 1 + case 2.2
if (root->left == nullptr) {
return root->right;
}
// case 2.1 + case 3
TreeNode* precursor = root->left;
while (precursor->right) {
precursor = precursor->right;
}
// 把 key 往后移,将 case 3 转为 case 1 或case 2
swap(root->val, precursor->val);
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
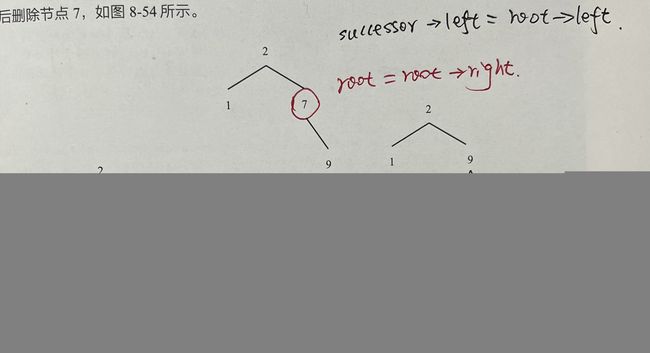
另一种直观好理解的方法,但是对数结构改变较大的方法:
// 待删除的节点为:
// case 1.叶子节点--直接删除
// case 2.只有左子树(case 2.1)或只有右子树(case 2.2)--子承父业
// case 3.左右子树都有--后继->left = root->left; root = root->right;
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
// 1.终止条件:没找到待删除节点
if (root == nullptr) return root;
// 2.前序遍历
if (key == root->val) { // 中
// case 1 + 2
if (root->left == nullptr) return root->right;
else if (root->right == nullptr) return root->left;
else {// case 3
// 找后继
TreeNode* successor = root->right; // 右拐一次
while (successor->left) { // 然后使劲左拐
successor = successor->left;
}
successor->left = root->left;
root = root->right;
return root;
}
}
if (key < root->val) root->left = deleteNode(root->left, key); // 左
if (key > root->val) root->right = deleteNode(root->right, key); // 右
return root;
}
};
记忆就记这个版本,最好记忆。