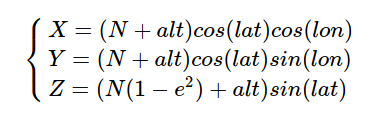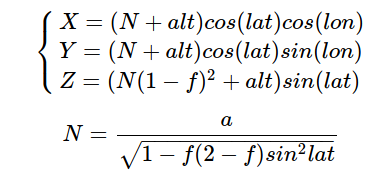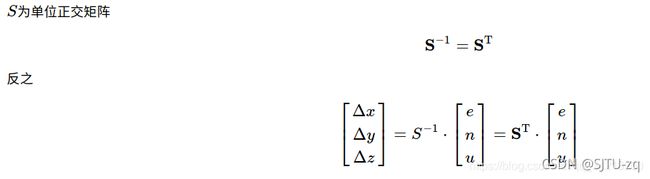无人驾驶-控制-坐标系转化

一、坐标系概念

1.1 WGS-84坐标系

1.1.1 简介

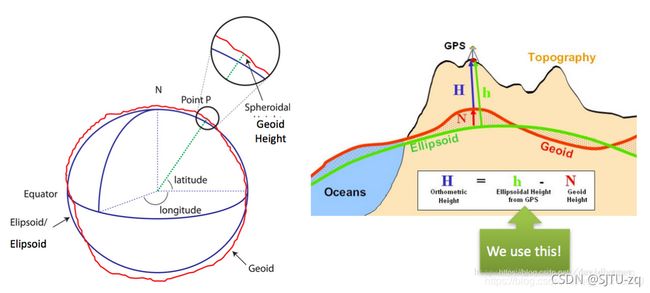
WGS84坐标系也叫经纬高坐标系【(经度(longitude)，纬度(latitude)和高度(altitude)】或者LLA坐标系，全球地理坐标系、大地坐标系。

作为广泛应用的一个地球坐标系，它给出一点的大地纬度、大地经度和大地高程而更加直观地告诉我们该点在地球中的位置，故又被称作经纬高坐标系。WGS-84坐标系的X轴指向BIH(国际时间服务机构)1984.0定义的零子午面(Greenwich)和协议地球极(CTP)赤道的交点。Z轴指向CTP方向。Y轴与X、Z轴构成右手坐标系。

1.1.2 角度范围

注：把ECEF坐标系用在GPS中时，就是WGS-84坐标系，在无人驾驶开发中，车载GPS提供的原始数据（LLA数据）就是WGS-84坐标系下的经纬高。
注意点
（1）：大地纬度是过用户点P的基准椭球面法线与赤道面的夹角。纬度值在-90°到+90°之间。北半球为正，南半球为负。

（2）：大地经度是过用户点P的子午面与本初子午线之间的夹角。经度值在-180°到+180°之间。

（3）：大地高度h是过用户点P到基准椭球面的法线距离，基准椭球面以内为负，以外为正。

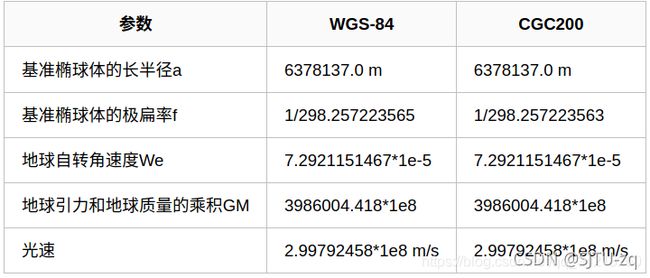
1.1.3 基本参数

基本参数

自然系数e：0.0818191908425；

1.1.4 坐标系图示

1.2 ECEF地心坐标系

1.2.1 简介

地心地固坐标系（Earth-Centered, Earth-Fixed，简称ECEF）简称地心坐标系，ECEF坐标系与地球固联，且随着地球转动，是一种以地心为原点的地固坐标系（也称地球坐标系），是一种笛卡儿坐标系。

ECEF坐标系是以地球为中心，是一个笛卡尔坐标系，也称为“普通地表”系统。是用来表示（X,Y,Z）坐标的位置，原点 O (0,0,0)为地球质心，z 轴与地轴平行指向北极点，x 轴指向本初子午线与赤道的交点，y 轴垂直于xOz平面(即东经90度与赤道的交点)构成右手坐标系。

1.2.2 坐标系图解

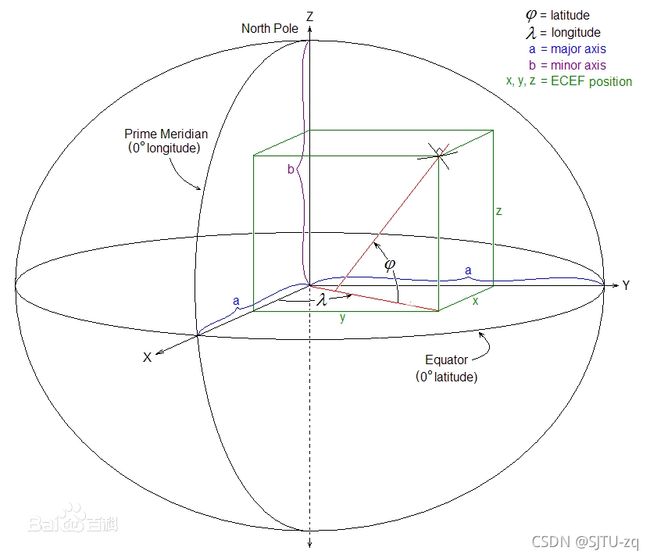
ECEF坐标系与WGS-84坐标系区别（结合上面WGS-84图）
（1）图中，φ、λ表示纬度和经度，是WGS84坐标系的参数；
（2）x、y、z为ECEF坐标系的描述，从图中可以看出，目标点（X）标记处在不同坐标系下描述的区别。

1.3 ENU东北天坐标系

1.3.1 简介

ENU坐标系也叫站心坐标系，是以用户当前所在位置点为坐标原点的坐标系。

坐标系定义为：
X轴：指向东边
Y轴：指向北边
Z轴：指向天顶

ENU局部坐标系采用三维直角坐标系来描述地球表面，实际应用较为困难，因此一般使用简化后的二维投影坐标系来描述。在众多二维投影坐标系中，统一横轴墨卡托（The Universal Transverse Mercator ，UTM）坐标系是一种应用较为广泛的一种。UTM 坐标系统使用基于网格的方法表示坐标，它将地球分为 60 个经度区，每个区包含6度的经度范围，每个区内的坐标均基于横轴墨卡托投影。

1.3.2 坐标系图解

从定义来分类，局部切线平面可分为基于垂直和水平尺寸定义的平面，主要表现在纵坐标为上还是下。纵坐标为上时，称为ENU（东、北、天）坐标系，主要用于地理方面；纵坐标为下时，称为NED（北、东、地）坐标系，特别用于航空航天。无人驾驶开发中，常用ENU（北、东、天坐标系），下文坐标系转化也是基于ENU坐标系。

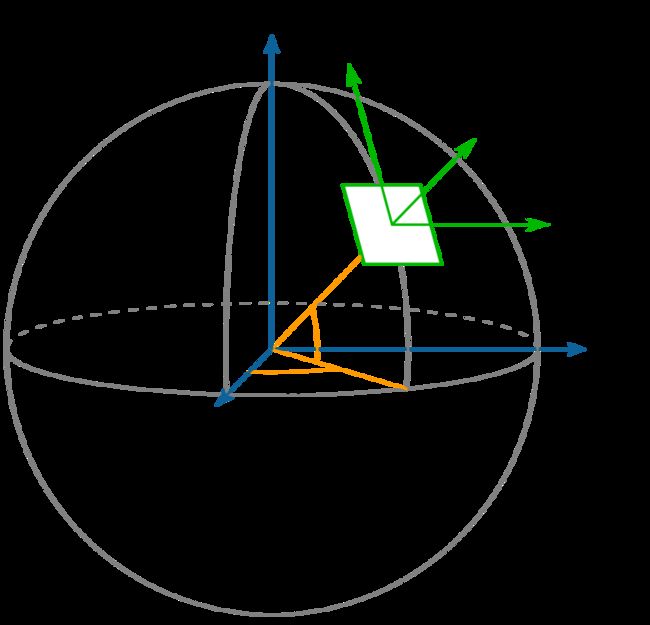
上图为ENU坐标系，该坐标系即为控制装置所在位置的“平面坐标系”，又称为地理坐标系。

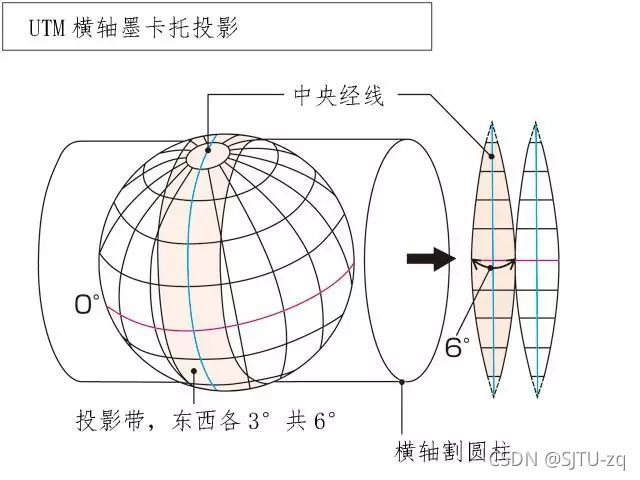
1.3.3 UTM坐标系

UTM（Universal Transverse Mercator Grid System，通用横墨卡托格网系统）坐标是一种平面直角坐标，这种坐标格网系统及其所依据的投影已经广泛用于地形图，作为卫星影像和自然资源数据库的参考格网以及要求精确定位的其他应用。

UTM坐标系与ENU坐标系区别
ENU局部坐标系采用三维直角坐标系来描述地球表面，实际应用较为困难，因此一般使用简化后的二维投影坐标系来描述。UTM坐标系在众多二维投影坐标系中，是一种应用较为广泛的坐标系。UTM坐标系使用基于网格的方法表示坐标，它将地球分为60个经度区，每个区包含6度的经度范围，每个区内的坐标均基于横轴墨卡托投影。

1.4 载体坐标系

1.4.1 简介

载体坐标系指的是以载体的质心为原点，OX沿纵轴方向，即载体前进方向，Z轴沿载体侧轴方向，指向右翼，Y沿载体竖轴方向，是右手坐标系而成（即指向天）。载体坐标系相对于地理坐标系的关系就是载体的姿态。导航的基本原则就是保证两个基本坐标系的正确转化，没有误差。只有实现了这个原则，载体才可以在自己的坐标系中完成一系列动作而被转换到地理坐标系中看起来是正确的。

在我们的实际控制当中，我们关心的是载体坐标系相对于地理坐标系之间的变化，所以我们通常使用的旋转矩阵是把“地理”坐标系转到“载体”坐标系的矩阵，从而实现对控制目标（载体）的姿态控制。由地理坐标系到载体坐标系的转换常用的有三种方式：四元数、欧拉角、方向余弦矩阵。

1.4.2 车辆坐标系

无人车上拥有各种各样的传感器，每个传感器的安装位置和角度又不尽相同。对于传感器的提供商，开始并不知道传感器会以什么角度，安装在什么位置，因此只能根据传感器自身建立坐标系。无人驾驶系统是一个多传感器整合的系统，需要将不同位置的传感器数据统一到一个固定的坐标系——自车坐标系下，才能分析当前无人车所在的道路场景。

一般情况下，由于车辆坐标系原点的高度和IMU的高度保持一致，且xy相交于两个前轮中心，通常就把IMU坐标系原点设为车辆坐标系原点，只是IMU坐标系和车辆坐标系的xy方向不一样，所以需要绕Z轴旋转90度，转化为车身坐标系。

IMU坐标系与车身坐标系XYZ方向：
IMU坐标系为东北天，或叫右前天，即车辆右侧为X，前轴方向为Y，朝天方向为Z；
（原点在IMU中心）

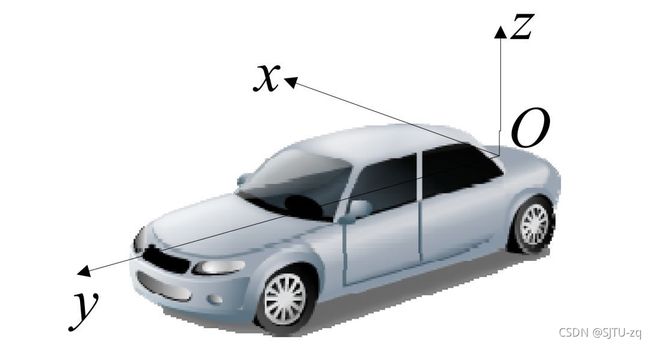
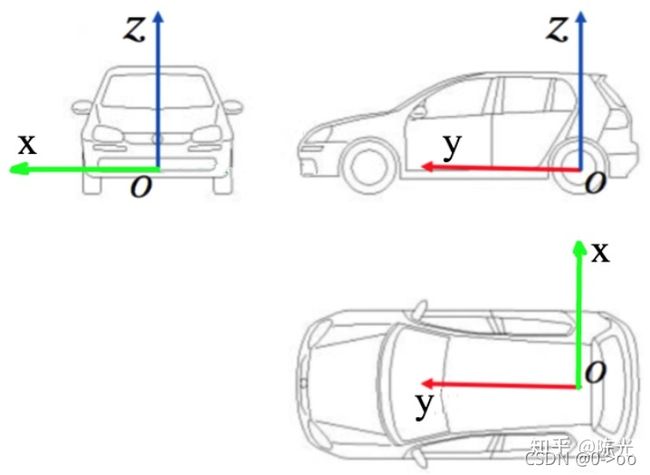
不同的无人驾驶团队对于坐标系的定义可能不同，但这并不影响开发，只要团队内部达成一致即可。以百度Apollo提供的自车坐标系为例，自车坐标系的定义为：

z轴 – 通过车顶垂直于地面指向上方

y轴 – 在行驶的方向上指向车辆前方

x轴 – 自车面向前方时，指向车辆右侧

车辆坐标系的原点在车辆后轮轴的中心，如下图所示。

1.4.3 S-L坐标系

SL坐标系也叫做frenet frame，以道路中心线为参考，S表示道路中心线的方向，L表示与道路中心线垂直的方向。在结构化道路上行驶的时候，SL坐标系比XY坐标系更加贴合实际需求。

S-L坐标系推导

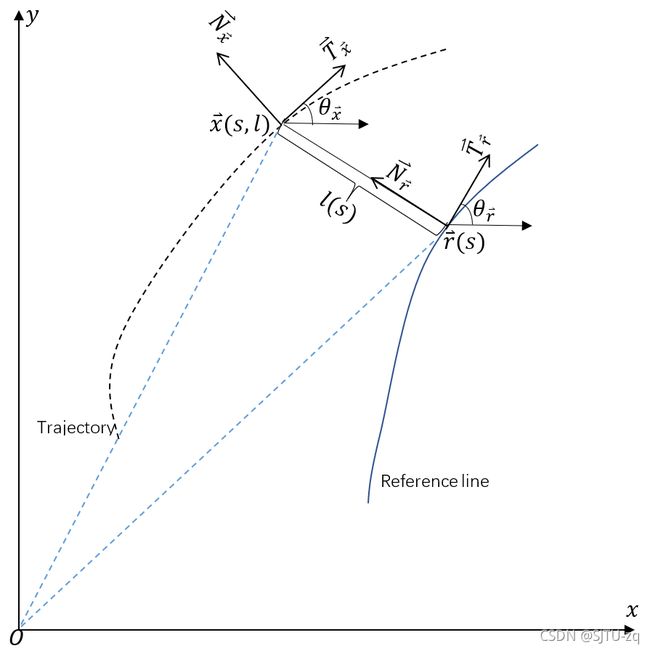
推导链接：https://blog.csdn.net/davidhopper/article/details/79162385

1.4.4 坐标系互转

开发过程中，我们经常遇到坐标系互相转换的要求，如将传感器坐标系与自车坐标系进行转换，以安装在无人车左前方的角雷达（Corner radar）为例，进行后面的介绍，叫雷达的安装位置和坐标系如下图绿线所示。

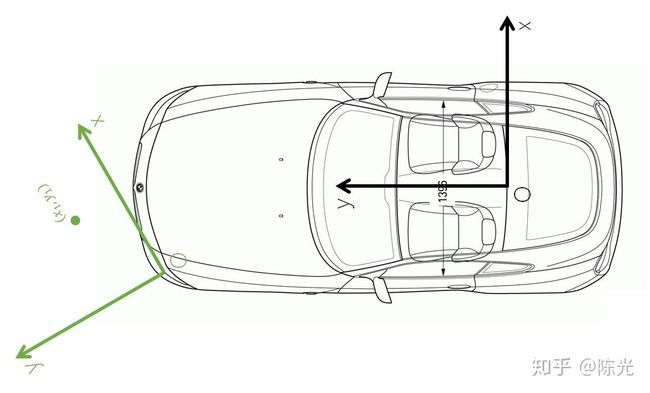
角雷达检测到的障碍物如图中的绿点所示，绿点在雷达坐标系下的坐标为(x1,y1），为了便于理解暂不加入z方向的坐标。绿点转换到自车坐标系下需要经过一定的数学运算。基本思路是这样的：

（1）平移

先将角雷达坐标系的O点平移到与自车坐标系的O点重合，此时(x1,y1)需要减去两个坐标系在x和y方向的距离。如下图所示

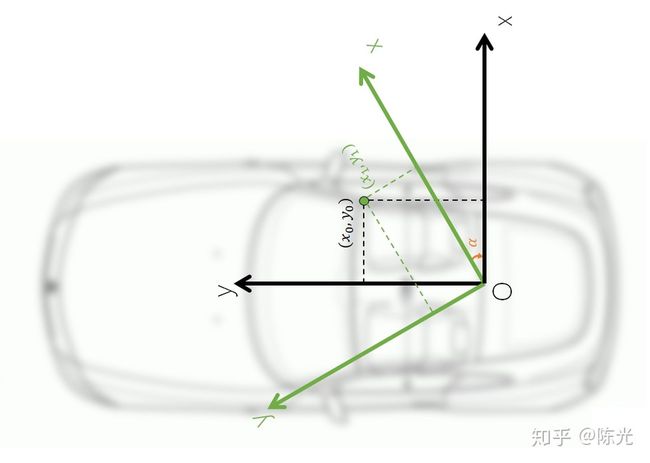
（2）旋转

在两个坐标系的O点重合后，将角雷达坐标系沿着z轴进行一定角度的旋转，这样(x1,y1)就转到了自车坐标系上。这个过程在数学上称为欧拉旋转。

（3）具体实现

• 平移

平移步骤根据传感器安装位置和自车后轴的距离进行计算，仅仅是XYZ三个方向加减运算。

• 旋转

绕轴旋转需要引入角度，不是简单的加减运算，所以我们通过图示来推导一下。先将两个坐标系变换到正常的视角，如下图所示：

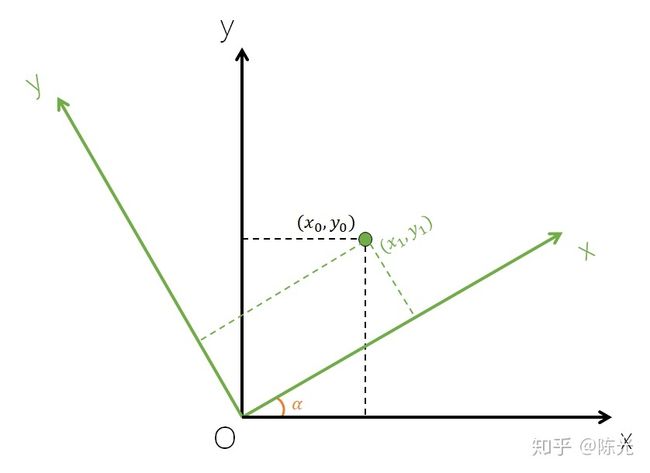
障碍物在角雷达坐标系下的坐标为(x1,y1)，假设障碍物在自车坐标系下的坐标为(x0,y0)，需要根据安装角度α（可测量），用x1，y1，α这三个已知量表示x0，y0，求得他们的数学关系。

通过做辅助线进行计算，如下图蓝线所示：

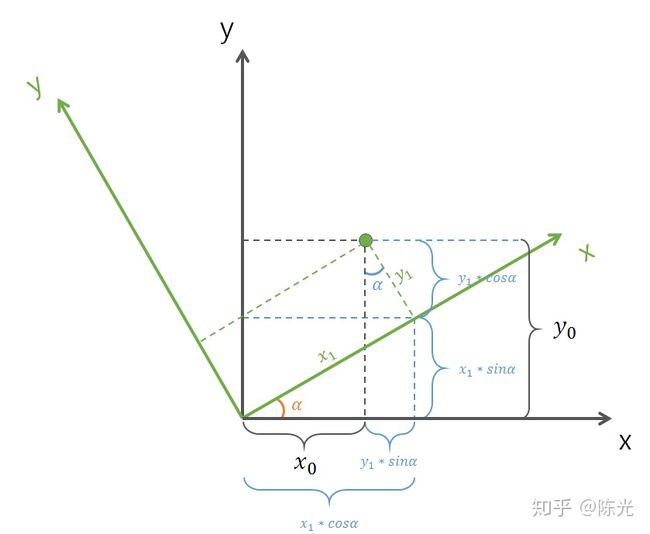
几何关系可用以下两个等式表示：

使用矩阵表示，可以简化表达，用一个等式代替两个等式：

（4）备注

由于这次旋转是绕z轴旋转，因此旋转前和旋转后的z值是保持不变的

将z方向的值也放到上面的等式中，即可得到

那就意味着，只要把角雷达采集到的障碍物坐标值与上面这个矩阵进行矩阵乘法运算，即可完成沿Z轴的旋转。在这里我们把这个矩阵叫做Z轴旋转矩阵RZ，那必然还有沿着X轴和Y轴的旋转矩阵RX和RY。角雷达目标的坐标依次右乘这三个矩阵，就完成了沿着Z轴，Y轴，X轴的旋转，得到的结果就是自车坐标系下的坐标值了。

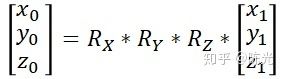
再加上一个平移的矩阵，就能够完整描述整个坐标转换的关系了

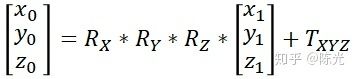
不同的坐标系定义，会有不同的RX，RY和RZ，因此需要根据实际情况计算旋转矩阵和平移矩阵。

二、坐标系转化

2.1 WGS84(LLA)-ECEF-ENU

2.1.1 WGS84-ECEF

（1）坐标转化公式

LLA坐标系下的(lon,lat,alt)转换为ECEF坐标系下点(X,Y,Z)

转换公式一

转换公式二

（2）基本参数

其中e为椭球偏心率，N为基准椭球体的曲率半径

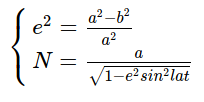
WGS-84下极扁率f 与偏心率e关系

（3）代码

// LLA->ECEF
	double R0 = 6378137.0;
    const double e = 0.0818191908425;
    const double torad = M_PI / 180;

    double Re = R0 / sqrt(1 - e * e * sin(ori_latitude * torad) * sin(ori_latitude * torad));
    double x0_ECEF = (Re + ori_height) * cos(ori_latitude * torad) * cos(ori_longitude * torad);
    double y0_ECEF = (Re + ori_height) * cos(ori_latitude * torad) * sin(ori_longitude * torad);
    double z0_ECEF = (Re * (1 - e * e) + ori_height) * sin(ori_latitude * torad); 

2.1.2 ECEF-ENU

（1）坐标转化公式

坐标原点P0（x0, y0, z0），计算点P（x, y, z）以P0为坐标原点的ENU坐标系位置，这里用到的P0的经纬度LLA（lon0, lat0, alt0）。

（2）代码

// ECEF->ENU
 	Re = R0 / sqrt(1 - e * e * sin(p.latitude * torad) * sin(p.latitude * torad));
    double dx_ECEF = (Re + p.height) * cos(p.latitude * torad) * cos(p.longitude * torad) - x0_ECEF;
    double dy_ECEF = (Re + p.height) * cos(p.latitude * torad) * sin(p.longitude * torad) - y0_ECEF;
    double dz_ECEF = (Re * (1 - e * e) + p.height) * sin(p.latitude * torad) - z0_ECEF;

    double x = -sin(p.longitude * torad) * dx_ECEF + cos(p.longitude * torad) * dy_ECEF;
    double y = -sin(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF - sin(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + cos(p.latitude * torad) * dz_ECEF;
    double z = cos(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF + cos(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + sin(p.latitude * torad) * dz_ECEF;

2.2 ENU-ECEF-WGS84(LLA)

2.2.1 ENU-ECEF

（1）公式转化

2.2.2 ECEF-WGS84

（1）公式转化

ECEF坐标系下点(X,Y,Z)转换为LLA坐标系下的(lon,lat,alt)

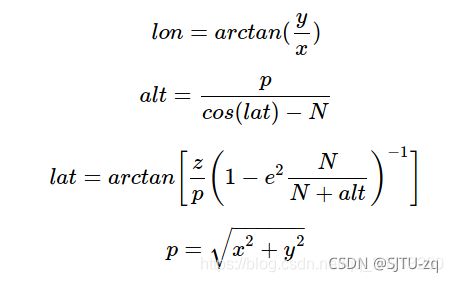
2.3 WGS84-ENU

（1）公式转化

上述可以看到，从LLA坐标系转换到enu坐标系有较多计算量，在考虑地球偏心率e ee很小的前提下，可以做一定的近似公式计算

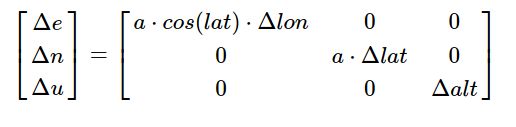
（2）代码

//LLA->ENU
void gps2xy(const &p, const double &ori_longitude, const double &ori_latitude, const double &ori_height)
{
    double R0 = 6378137.0;
    const double e = 0.0818191908425;
    const double torad = M_PI / 180;

    double Re = R0 / sqrt(1 - e * e * sin(ori_latitude * torad) * sin(ori_latitude * torad));
    double x0_ECEF = (Re + ori_height) * cos(ori_latitude * torad) * cos(ori_longitude * torad);
    double y0_ECEF = (Re + ori_height) * cos(ori_latitude * torad) * sin(ori_longitude * torad);
    double z0_ECEF = (Re * (1 - e * e) + ori_height) * sin(ori_latitude * torad);

    Re = R0 / sqrt(1 - e * e * sin(p.latitude * torad) * sin(p.latitude * torad));
    double dx_ECEF = (Re + p.height) * cos(p.latitude * torad) * cos(p.longitude * torad) - x0_ECEF;
    double dy_ECEF = (Re + p.height) * cos(p.latitude * torad) * sin(p.longitude * torad) - y0_ECEF;
    double dz_ECEF = (Re * (1 - e * e) + p.height) * sin(p.latitude * torad) - z0_ECEF;

    // ECEF to ENU
    double x = -sin(p.longitude * torad) * dx_ECEF + cos(p.longitude * torad) * dy_ECEF;
    double y = -sin(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF - sin(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + cos(p.latitude * torad) * dz_ECEF;
    double z = cos(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF + cos(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + sin(p.latitude * torad) * dz_ECEF;
}

参考链接

1. https://www.cnblogs.com/ethanda/p/10325109.html
2. https://blog.csdn.net/qq_34213260/article/details/109133847
3. https://blog.csdn.net/u011754972/article/details/117122975
4. https://blog.csdn.net/qq_45577461/article/details/107931195
5. https://blog.csdn.net/davidhopper/article/details/79162385
6. https://blog.csdn.net/jinking01/article