自己动手实现一个全连接神经网络模型

代码实现

激活函数函数实现

神经网络模型中常用的激活函数有Sigmoid, Relu, Tan，本文对首先对各个激活函数机器激活函数求偏导进行实现：

#各个激活函数实现
def no_activate(x):
	return x
	
def relu(x):
    return np.max(0, x)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def tan(x):
    return np.tanh(x)

#各个激活函数的求偏导实现
def no_activate_derive(x):
	return 1
	
def relu_derive(x):
    result = np.zeros_like(x)
    result[x > 0] = 1

    return result

def sigmoid_derive(x):
    return sigmoid(x)*(1-sigmoid(x))

def tan_derive(x):
    return 1 - x**2

单层网络实现

构造单层类，通过组合，可以非常方便地创建任意形状地神经网络。

#单层模型
class Layer:
    def __init__(self, input_num, output_num, activate_func, activate_derive_func, weight = None, bias = None):
        #初始化w参数
        #self.weights = np.random.normal(loc=0, scale=1, size=(input_num, output_num))
        self.weights  = np.random.randn(input_num, output_num) * np.sqrt(1/output_num)
        self.bias = np.random.randn(1, output_num) * 0.1
        #初始化b参数
        #self.bias = np.zeros(shape=(output_num)).reshape(1, output_num)
        #对于w的偏导
        self.dw = None  
        #对于b的偏导
        self.db = None
        self.activate_func = activate_func
        self.activate_derive_func = activate_derive_func
        self.x = None
        self.z = None
        self.cache = None

    
    #前向传播算法
    def foward(self, input):
        #缓存输入值
        self.x = input
        #计算z = wx+b
        z = np.dot(input, self.weights) + self.bias
         #缓存z值,后续反向传播中求导需要用到
        self.z = z
        #进行激活，并缓存激活值
        activate_value = self.activate_func(z)
       
        return activate_value

    #反向传播算法
    def backward(self, input):
        #对z求导 (dz矩阵的shape为 1 * output_num)
        dz = input * self.activate_derive_func(self.z)
        print(dz.shape)
        #对w进行求导(dw矩阵的shape为input_num * output_num)
        self.dw = np.dot(self.x.T, dz)
        #对b进行求导(db的shape为1 * output_num)
        self.db = dz
        #缓存本层的求导中间值，作为反向传播中下一层的输入值
        self.cache = np.dot(dz, self.weights.T)

        return self.cache
        
    #更新w参数与b参数
    def update(self, learning_rate):
        self.weights -= learning_rate * self.dw
        self.bias -= learning_rate * self.db

全连接神经网络模型实现

构造网络模型，网络模型类与单层类是组合关系

#神经网络模型
class NeuralNetwork:
    def __init__(self, learning_rate):
        self.layers = []
        self.learning_rate = learning_rate

    #增加一层网络
    def add_layer(self, layer):
        self.layers.append(layer)
    
    #前向传导
    def forwar_calcuate(self, x):
        #逐层前向传播
        for layer in self.layers:
            x = layer.foward(x)
        return x

    #反向传播
    def backward_calculate(self, x, y):
    	#先进行一遍前向传播
        output = self.forwar_calcuate(x)
        output = output - y
        
        #反向遍历整个网络，对每一层做backward操作
        for i in reversed(range(len(self.layers))):
            layer = self.layers[i]
            output = layer.backward(output)
		
		#更新每一层的w参数和b参数，使其更接近真实值
        for layer in self.layers:
            layer.update(self.learning_rate) 

    #训练
    def train(self, x_train, y_train, epochs):
    	#先将数据进行one-hot转换，方便训练
        y_one_hot = np.zeros((y_train.shape[0], 2))
        y_one_hot[np.arange(y_train.shape[0]), y_train] = 1
        mses = []
		
		#进行epochs次迭代训练
        for i in range(epochs):
            y_predict = self.forwar_calcuate(x_train)
            #每次迭代之后都记录一下误差均值
            mse = np.mean(np.square(y_one_hot - y_predict))
            mses.append(mse)
            #每迭代10次打印一遍误差均值
            if i % 10 == 0:
                print('epcho:{}, mse:{}'.format(i, mse))
                #pass
			#逐个数据进行训练（可优化为batch训练方式）
            for j in range(len(x_train)):
                self.backward_calculate(x_train[j].reshape((1,2)), y_one_hot[j].reshape((1,2)))

        plt.plot(mses)

    #打印模型预测准确率
    def accurancy(self, x_test, y_test):
        y_test_one_hot = np.zeros((y_test.shape[0], 2))
        y_test_one_hot[np.arange(y_test.shape[0]), y_test] = 1
        y_predict_one_hot = np.zeros_like(y_test_one_hot)

        for i in range(len(x_test)):
            y_predict = self.forwar_calcuate(x_test[i])
            y_predict_one_hot[i][np.argmax(y_predict)] = 1
        
        right_count = 0
        for i in range(len(x_test)):
            if (y_predict_one_hot[i] == y_test_one_hot[i]).all():
                right_count += 1

        print("network auccurency:{}".format(right_count / len(x_test)))

到此一个任意层的神经网络模型就实现完毕，下面我们利用sklearn提供的数据集对这个神经网络进行验证。

数据集加载

import numpy as np
import os
import matplotlib.pyplot as plt
#这里使用make_moons数据集
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
%matplotlib inline

SAMPLE_COUNT = 3000

#加载数据集（首次调用需要从远程下载数据集，会比较慢）
x, y = make_moons(n_samples=SAMPLE_COUNT, noise=0.2)
#这里将数据集分为训练集与测试集，训练时采用训练集数据进行训练，验证时采用测试集数据进行验证
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
x_train.shape, y_train.shape, x_test.shape, y_test.shape

#利用matplotlib绘制图形
def make_plot(x, y, plot_name, file_name = None):
    plt.style.use('dark_background')
    plt.figure(figsize=(16,12))
    plt.title(plot_name, fontsize = 30)
    plt.scatter(x[:, 0], x[:, 1], c = y.ravel(), s=40)
    plt.show()

我们先来看下数据集中的数据分布

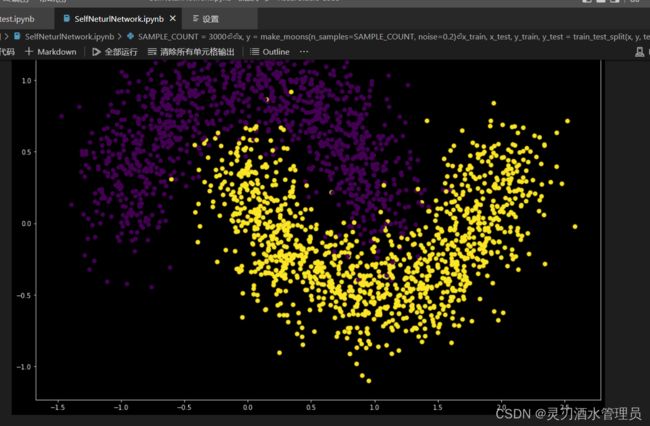
通过数据分布图可以看出，该数据是典型的线性不可分数据，而我们的目标就是给定输入
(x1(横轴), x2(纵轴))，能供通过神经网络实例准确预测出类别(黄色or紫色)。

进行训练与预测

接下来我们就开始利用整个网络模型进行数据训练吧：

#初始化神经网络中的每一层网络
layer1 = Layer(2, 25, sigmoid, sigmoid_derive)
layer2 = Layer(25, 50, sigmoid, sigmoid_derive)
layer3 = Layer(50, 25, sigmoid, sigmoid_derive)
layer4 = Layer(25, 2, sigmoid, sigmoid_derive)

#设置学习率为0.01
network = NeuralNetwork(0.01)

#构造神经网络(2 * 25 * 50 * 25 * 2 层神经网络模型，激活函数使用sigmoid激活函数)
network.add_layer(layer1)
network.add_layer(layer2)
network.add_layer(layer3)
network.add_layer(layer4)

#打印图像
make_plot(x_train, y_train, "moon plot")

#进行训练(迭代500次)
network.train(x_train, y_train, 500)
#利用测试集测试准确率
network.accurancy(x_test, y_test)

模型性能统计

准确率与误差统计（横轴为迭代次数，纵轴为误差值）：

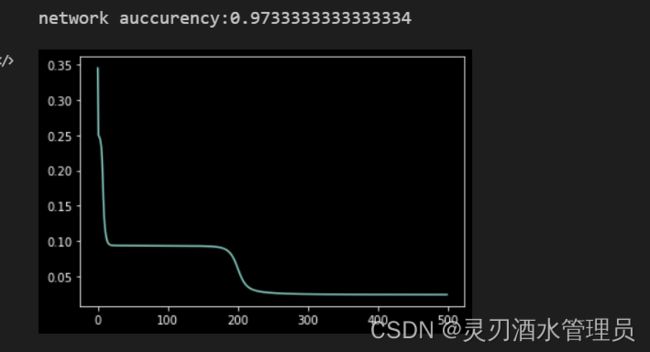
由上图可以看到，经过500次迭代后，我们这个模型对于测试集上的数据预测，准确率达到了97%以上，当然通过调整学习率，也许可以让模型的性能变得更加优秀，但是这不属于本文的讨论与实现范围了。

数学推导

下面我们就结合代码来简单聊一下神经网络模型中用到的几个非常重要的数学性质。

梯度下降

为了简化讨论，我们来拿单条数据预测为例。假设我们模型预测出来的数据为y，而该数据的真实标签值为t（注意，这里的y与t都为向量），那么y与t的误差我们可以用
$$Loss=(y-t{)}^2/2$$

这里除以2完全是为了后面求导方便。模型训练的目标就是要让该值能够尽量小，而y又是关于模型参数w和b的函数，根据凸函数的性质，该表达式的最小值一定是在w和b的偏导数的值为0的产生。

但遗憾的是，w和b关于y的偏导表达式我们无法通过数学解析式直接求出。但我们可以通过偏导函数的定义，找到一种迭代的方式，在每次迭代的过程中，通过不断调整w和b的值，逐步使表达式的值减小。那该如何调整w和b的值呢，我们知道偏导数的定义就是函数针对某个变量的变化率，那么只要我们的变量沿着该导数相反的方向变化，那么一定能让表达式的值逐渐靠近最小值，这就是梯度下降的原理。用公式来表达就是每次迭代过程中，让
$$w=w-\eta \ast \frac{\partial Loss}{\partial w}（\eta 为步长，也称作学习率）$$
$$b=b-\eta \ast \frac{\partial Loss}{\partial b}（\eta 为步长，也称作学习率）$$
就可以逐步减小Loss的值了。在代码中

    #更新w参数与b参数
    def update(self, learning_rate):
        self.weights -= learning_rate * self.dw
        self.bias -= learning_rate * self.db

就是在做这件事情。

链式求导法则

说完梯度下降，我们再来聊聊链式求导法则。假设y是关于xn的函数，xn是关于xn-1的函数，xn-1是关于xn-2的函数…。链式求导法则定理是：
$$\frac{\partial y}{\partial x_1}=\frac{\partial y}{\partial x_n}\ast \frac{\partial x_n}{\partial x_{n-1}}\ast ......\ast \frac{\partial x_2}{\partial x_1}$$
我们知道在神经网络的正向传播中，每一层都是由一个wx+b的表达式以及激活函数组成。
用数学表达式可以这么表达(以3层网络模型为例)：
$$z1=w_{1}x+b1$$ $$a1=activate(z1)$$$$z_2=w_2{a}_1+b_2$$$$a_2=activate(z_2)$$$$z_3=w_3{a}_2+b_3$$$$a_3=activate(z_3)$$$$Loss=(a_3-t{)}^2/2$$。
我们的目标是对w1,w2,w3,b1,b2,b3关于Loss求偏导。显然，直接通过数学解析是肯定求不出来的，但是我们可以利用链式求导针求出各个参数的导数值，具体来说就是：
$$（1）\frac{\partial Loss}{\partial w_3}=\frac{\partial Loss}{\partial a_3}\ast \frac{\partial a_3}{\partial z_3}\ast \frac{\partial z_3}{\partial w_3}$$
。其中右边的每一项我们都是可求的。
同理：
$$（2）\frac{\partial Loss}{\partial w_2}=\frac{\partial Loss}{\partial a_3}\ast \frac{\partial a_3}{\partial z_3}\ast \frac{\partial z_3}{\partial a_2}\ast \frac{\partial a_2}{\partial z_2}\ast \frac{\partial z_2}{\partial w_2}$$
剩下的b3,b2,b1,w1等参数也可以通过这种方法求出。通过观察，（2）式中有一部分的内容与（1）式中完全相同，因此我们在编写代码的过程中，在求（2）的过程中，完全可以利用（1）中已经求得的数据直接进行运算，这样能够大大减少重复计算。

    #反向传播算法
    def backward(self, input):
        #对z求导 (dz矩阵的shape为 1 * output_num)
        dz = input * self.activate_derive_func(self.z)
        print(dz.shape)
        #对w进行求导(dw矩阵的shape为input_num * output_num)
        self.dw = np.dot(self.x.T, dz)
        #对b进行求导(db的shape为1 * output_num)
        self.db = dz
        #缓存本层的求导中间值，作为反向传播中下一层的输入值
        self.cache = np.dot(dz, self.weights.T)

        return self.cache

具体在上面代码中，input就是我们在反向传播过程中，上一个求导表达式返回的数据就是（2）与（1）中重叠计算的部分。

写在最后

虽然在目前的深度学习框架过程中，pytorch、tensorflow2.0、padlepadle这些框架都通过非常优雅的封装实现了自动求梯度，自动正向反向传播，甚至连参数设置对使用者来说都是透明的。但是我依然觉得不依赖任何框架的内容，完全手动实现一遍全连接神经网络的实现式非常有意义的。在这个过程中，非常有利于自己对于正向、反向传播以及超参数的设置，激活函数的选择等细节的理解。并且在后续使用框架编写神经网络的过程中，也能够更好地对目前市面上这些框架背后的原理有更深入的理解。而全连接网络也是后面理解卷积神经网络、对抗神经网络的基础。而目前人工智能中最热门的领域之一强化学习，也在跟深度学习绑定的越来越紧密，我们熟知的AlphaGo的强化学习算法，就是通过深度学习训练策略网络与价值网络，完成了超越人类顶级专家水准的学习。
作为一名游戏从业人员，深度强化学习在游戏领域表现得也是越来越出彩，在了解到网易伏羲实验室的一些成果后，也坚定了自己向这个方向靠拢的决心，后面我也会通过不断地学习总结学习地方式，与大家分享探讨一些人工智能方面的理论知识与实践应用，而下一篇的内容我也规划好了，就是利用深度强化学习进行我们小的时候完的街机游戏的训练，不过市面上很多对于游戏的实现都是通过机器视觉，分析画面像素的方式进行，这种发放时虽然很通用（完全不用思考如何设置状态，状态就是三通道的像素），但一是训练速度慢，二是很难工业化落地。因此我还在探索一种通过自定义状态进行训练，也为今后能够将强化学习应用到mmorpg这种类型的游戏中打好基础。