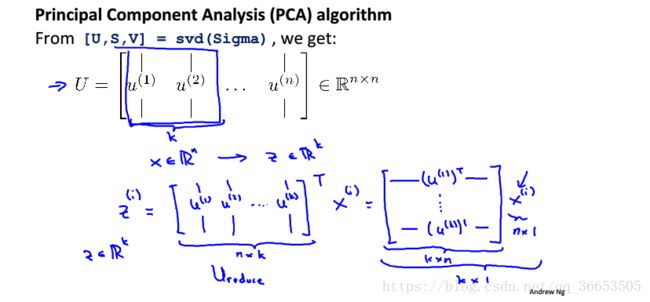
机器学习之主成分分析（PCA）

降维的目的

1. 进行数据降维处理，我们可以容易地实现高维数据可视化——将其降为三维甚至二维。
2. 由于可能存在许多冗余特征量，所以需要减少特征量的数量。（比如同时有英寸和米的数据，这样的数据是线性相关的，可以去掉其中之一）
3. 机器学习算法的复杂度和数据的维数有着密切关系，甚至与维数呈指数级关联。因此我们必须对数据进行降维。

降维的方法

在机器学习领域，我们对原始数据进行特征提取，有时会得到比较高维的特征向量。在这些向量所处的高维空间中，包含很多的冗余和噪声。我们希望通过降维的方式来寻找数据内部的特性，从而提高特征的表达能力，降低训练复杂度。
主要有三种方法：1）主成分分析（PCA）；2）因子分析（FA）；3）独立成分分析（ICA）。其中 PCA是一种具有严格数学基础并且已被广泛采用的降维方法。它属于一种线性、无监督、全局的降维方法。

PCA的理论基础和思想

1. PCA理论中，主要是用到线性代数中的特征值和特征向量。（详情可参考本博主的特征值和特征向量的几何意义的博文）
2. PCA的目标是降低每一个特征量到投影直线的距离，也就是降低投影误差。
3. PCA深入浅出的基本思想讲解还可参考吴恩达老师的《机器学习课程》
4. 用到的统计中的概念：均值、方差和协方差矩阵

给定一个含有m个样本的集合：X={X1,…,Xm}
均值：

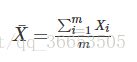
方差：

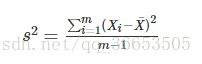
均值描述的是样本集合的平均值，方差描述的是样本集合中各个点到均值的距离的平均，也就是数据的离散程度。

如果数据的维数比较多的话，我们想知道某两个特征之间是否有关系，比如说统计学生的成绩，数学成绩和物理成绩

之间是否有关系，如果有是正相关呢还是负相关，协方差就是用来描述两个随机变量X,Y之间关系的统计量，协方差

定义如下：

协方差的结果为正的话，表明二者之间是正相关，为负的话表明二者之间是负相关。这里的X,Y两个一维的随机变量，

如果随机变量的个数很多呢，这时候就引入了协方差矩阵的概念：对于一个n维的数据，分别计算每两个维度之间的协方差，就构成了一个协方差矩阵：

可见这是一个对称矩阵，对角线上的是方差。如果数据是三维的，则协方差矩阵如下：

PCA算法实现过程推导

• 给定一个训练集$x^1$，$x^2$，…，$x^m$。其中m表示样本数量，$x^i$是表示i样本的n维特征向量（为列向量）
  $$x^{(i)}=\left(\begin{array}{c}{x}_1^{(i)}\\ x_2^{(i)}\\ .\\ .\\ .\\ x_n^{(i)}\end{array}\right)$$

• 对数据进行预处理（特征缩放，均值为零）
  $${\mu }_j=\frac{1}{m}\sum _{i=1}^m{x}_j^{(i)}$$
  用$x_j^{(i)}-{\mu }_j$来代替原来的特征$x_j^{(i)}$

• 构造协方差矩阵，对于单个样本i
  $$cov=(x^{(i)})(x^{(i)}{)}^T$$
  对所有样本的协方差矩阵，就是对所有样本求个平均值
  $$C=\frac{1}{m}\sum _{i=1}^m(x^{(i)})(x^{(i)}{)}^T$$

  设所有样本组成的矩阵为A
  $$A=\left(\begin{array}{cccc}|& |& |& |\\ x^{(1)}& x^{(2)}& \cdots & x^{(m)}\\ |& |& |& |\end{array}\right)$$
  则
  $$C=\frac{1}{m}A{A}^T$$

• 对协方差矩阵进行特征值分解或者直接使用奇异值分解（SVD），如下图（来组吴恩达老师机器学习课件）：
  

• 最后使用选取的特征向量（这些特征向量构成了低维的子空间），对特征进行降维，如下图（同样来自吴恩达老师课件）：

最大方差理论推导PCA

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如前面的图，样本在横轴上的投影方差较大，在纵轴上的投影方差较小，那么认为纵轴上的投影是由噪声引起的。所以我们认为最好的k维特征是将n维的样本点转化之后，每一维上的样本方差都很大。
比如下图右5个样本点，所有的点已经做过预处理，均值为0，特征方差归一。

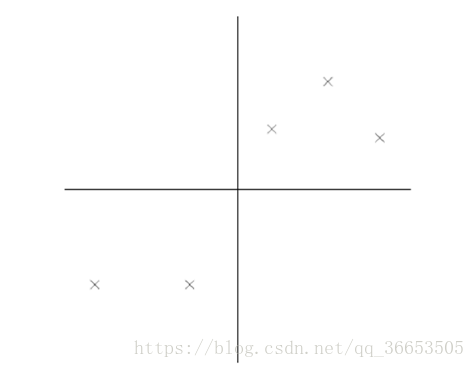
对与这样的一个二维平面上的点，我们现在想要把它投影到一个一维中去，也就是找到一条直线，将这些点全部投影到直线上去，达到降维的目的。下面是两条直线的比较

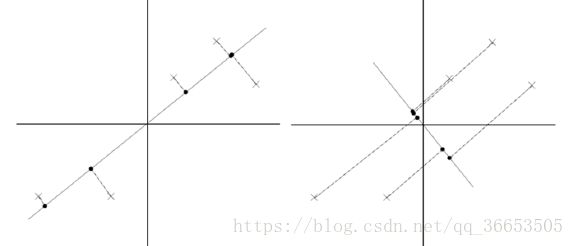
很明显，左边那条直线的投影效果更好，数据的方差更大，越有利于分类。

如图所示，红色的点表示的是样本点，蓝色的点表示的是样本点在向量u上的投影点，这里规定u是单位向量，则x在u上的投影可以表示为$x^{T}u$，假设现在有很多个样本点x，我们希望存在这样的一个u使得这些样本点投影到u上之后方差最大。由于样本点的每一维特征的均值都是0，所以投影到u上之后的样本点的均值也是0。
计算方差：
$$D(x)=\frac{1}{m}\sum _{i=1}^m(x^{(i{)}^T}u{)}^2=\frac{1}{m}\sum _{i=1}^m{u}^T{x}^{(i)}{x}^{(i{)}^T}u=u^T(\frac{1}{m}\sum _{i=1}^m{x}^{(i)}{x}^{(i{)}^T})u$$

其中$D(x)$表示所有样本的投影方差。很显然，中间括号的那一部分就是所有样本的协方差矩阵，唯一不同的地方就是协方差计算的时候是除m-1，这里是除m。好了，现在的目标就是要最大化这个式子，用$\sum$表示协方差，用$\lambda$表示优化目标，那么上述问题可以写成：

两边同时乘以u，u是单位向量，所以右边$u^{T}u$相乘的结果是1，变成

也就是

所以，最大化方差，即最大化$\lambda$，就是求解协方差矩阵的最大特征值，最佳投影方向就是最大投影值所对应的特征向量。次佳投影方向位于最佳投影方向的正交空间，是第二大特征值对应的特征向量，以此类推。

要选择多少个主成分，就意味着就选择多少个特征向量构成的子空间对数据进行降维。对于要选择的主成分（特征向量）数量，可用下式计算：
$$\eta =\sqrt{\frac{{\sum }_{i=1}^k{\lambda }_i^2}{{\sum }_{i=1}^n{\lambda }_i^2}}$$

其中k为选择的特征向量的数量，即为子空间的维数，n为每个样本的特征维数。

或者用最小平方误差理论推导PCA

这里省略最小平方误差理论的推导，一般理解最大方差理论就够啦。。。。

PCA算法实现（python）

以吴恩达老师的《机器学习》课程关于PCA的作业为例：

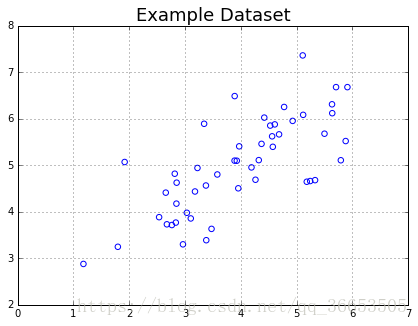
1. 展示数据

datafile = 'data/ex7data1.mat'
mat = scipy.io.loadmat( datafile )
X = mat['X']

#Quick plot
plt.figure(figsize=(7,5))
plot = plt.scatter(X[:,0], X[:,1], s=30, facecolors='none', edgecolors='b')
plt.title("Example Dataset",fontsize=18)
plt.grid(True)

2. 实现PCA

## 特征归一化
def featureNormalize(myX):
    #Feature-normalize X, return it
    means = np.mean(myX,axis=0)
    myX_norm = myX - means
    stds  = np.std(myX_norm,axis=0)
    myX_norm = myX_norm / stds
    return means, stds, myX_norm

## 使用SVD分解求解特征值和特征向量
def getUSV(myX_norm):
    # Compute the covariance matrix
    cov_matrix = myX_norm.T.dot(myX_norm)/myX_norm.shape[0]
    # Run single value decomposition to get the U principal component matrix
    U, S, V = scipy.linalg.svd(cov_matrix, full_matrices = True, compute_uv = True)
    return U, S, V

# Feature normalize
means, stds, X_norm = featureNormalize(X)
# Run SVD
U, S, V = getUSV(X_norm)

# "...output the top principal component (eigen- vector) found, 
# and you should expect to see an output of about [-0.707 -0.707]"
print 'Top principal component is ',U[:,0]

#Quick plot, now including the principal component
plt.figure(figsize=(7,5))
plot = plt.scatter(X[:,0], X[:,1], s=30, facecolors='none', edgecolors='b')
plt.title("Example Dataset: PCA Eigenvectors Shown",fontsize=18)
plt.xlabel('x1',fontsize=18)
plt.ylabel('x2',fontsize=18)
plt.grid(True)
#To draw the principal component, you draw them starting
#at the mean of the data
plt.plot([means[0], means[0] + 1.5*S[0]*U[0,0]], 
         [means[1], means[1] + 1.5*S[0]*U[0,1]],
        color='red',linewidth=3,
        label='First Principal Component')
plt.plot([means[0], means[0] + 1.5*S[1]*U[1,0]], 
         [means[1], means[1] + 1.5*S[1]*U[1,1]],
        color='fuchsia',linewidth=3,
        label='Second Principal Component')
leg = plt.legend(loc=4)

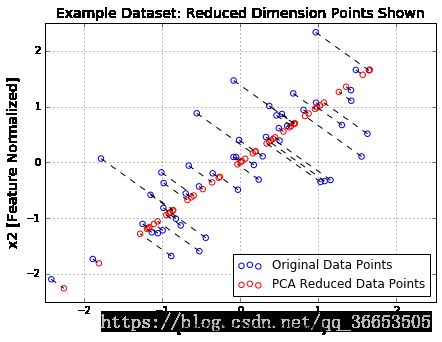
3. 降维

def projectData(myX, myU, K):
    """
    Function that computes the reduced data representation when
    projecting only on to the top "K" eigenvectors
    """
    
    #Reduced U is the first "K" columns in U
    Ureduced = myU[:,:K]
    z = myX.dot(Ureduced)
    return z

# "...project the first example onto the first dimension 
# "and you should see a value of about 1.481"
z = projectData(X_norm,U,1)
print 'Projection of the first example is %0.3f.'%float(z[0])


def recoverData(myZ, myU, K):
    Ureduced = myU[:,:K]
    Xapprox = myZ.dot(Ureduced.T)  
    return Xapprox

#Quick plot, now drawing projected points to the original points
plt.figure(figsize=(7,5))
plot = plt.scatter(X_norm[:,0], X_norm[:,1], s=30, facecolors='none', 
                   edgecolors='b',label='Original Data Points')
plot = plt.scatter(X_rec[:,0], X_rec[:,1], s=30, facecolors='none', 
                   edgecolors='r',label='PCA Reduced Data Points')

plt.title("Example Dataset: Reduced Dimension Points Shown",fontsize=14)
plt.xlabel('x1 [Feature Normalized]',fontsize=14)
plt.ylabel('x2 [Feature Normalized]',fontsize=14)
plt.grid(True)

for x in xrange(X_norm.shape[0]):
    plt.plot([X_norm[x,0],X_rec[x,0]],[X_norm[x,1],X_rec[x,1]],'k--')
    
leg = plt.legend(loc=4)

#Force square axes to make projections look better
dummy = plt.xlim((-2.5,2.5))
dummy = plt.ylim((-2.5,2.5))

后记

降维是通过低维的向量更好的表示特征。。与神经网络中的稀疏编码表示输入向量在思想上有相似之处。

参考

1. https://www.cnblogs.com/lzllovesyl/p/5235137.html
2. https://blog.csdn.net/zhongkelee/article/details/44064401（最大方差理论详细推导）
3. https://blog.csdn.net/YZXnuaa/article/details/80746287
4. https://blog.csdn.net/aiiyouwei/article/details/80173658
5. https://blog.csdn.net/huang1024rui/article/details/46662195
6. https://www.zhouyongyi.com/andrew-ng-machine-learning-notes-10/
7. https://blog.csdn.net/zouxy09/article/details/8775518