数学建模更新的所有作业实战

一.粒子算法

% 目标函数参考的最优值：38.8503    
narvs = 2; % 变量个数
x_lb = [-3 4.1]; % x的下界
x_ub = [12.1 5.8]; % x的上界

%% 直接使用particleswarm函数
[x,fval] = particleswarm(@fun6,narvs,x_lb,x_ub)
fval = -fval
x1=(-3:0.001:12.1);
x2=(4.1:0.001:5.8);
y=21.5+x1*sin(4*pi*x1)+x2*sin(20*pi*x2);
plot(x1,y,'-')

%% 将粒子群算法得到的解作为初始值，继续调用fmincon函数求解
options = optimoptions('particleswarm','HybridFcn',@fmincon);
[x,fval] = particleswarm(@fun6,narvs,x_lb,x_ub,options)
fval = -fval

%% 修改参数：这里要增加粒子个数，因为函数局部最小值太多了
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',20000,'SwarmSize',1000);
[x,fval] = particleswarm(@fun6,narvs,x_lb,x_ub,options)
fval = -fval 

不管咋调都差不多，哭泣

二.蒙特卡罗模拟

1.估算自然常数e

%%  作业参考答案：蒙特卡罗的方法去估计自然常数e
%% （1）预备知识
% (1)randperm函数的用法
randperm(5)  % 生成1-5组成的一个随机序列
%      3     5     1     2     4
%      1     4     5     3     2

% (2)find函数的用法 （第一期视频第一讲）
% 假设a是一个向量，那么find(a)可以用来返回这个向量中非零元素的下标，如果a中所有元素都为0，则返回空值
find([1,5,6,0,8,0,-5])  %      1     2     3     5     7
find([0,0,0,0,0])  %   空的 1×0 double 行矢量

% (3) 矩阵（或向量）和常量的比较运算可返回逻辑矩阵（或向量）(元素全为0和1)
[1,5,6,0,8,0,-5] > 0      %    1   1   1   0   1   0   0
[1,5,6,0,8,0,-5] == 0    %    0   0   0   1   0   1   0

% (4) isempty(A)函数可以用来判断A是否为空, 如果A为空， isempty(A) 返回逻辑值1(true)，否则返回逻辑值0(false)。
isempty(find([0,0,0,0,0]))   %    1
isempty(find([0,1,0,0,0]))   %    0
isempty([0,0,0,0,0])  % 注意，别搞错啦，它不是空矩阵（空矩阵是指里面没有元素）


%% （2）参考答案
clear;clc
tic  %计算tic和toc中间部分的代码的运行时间
n = 1000000;  % 蒙特卡洛的次数（理论上n取得越大，计算出来的结果越精确）
m = 0;   % 每个人拿到的都不是自己卡片的次数（频数）
people = 100;   % 假设一共有100个人玩这个游戏 （任给的）
for i = 1: n  % 开始循环
    if isempty(find(randperm(people) - [1:people] == 0))  % 如果每个人拿到的都不是自己的卡片
        m = m + 1;  % 那么次数就加1
    end
end
frequency = m / n;  % 每个人拿到的都不是自己卡片的频率（概率）
disp(['自然常数e的蒙特卡罗模拟值为：', num2str(1 / frequency)])  % 注：自然常数真实值约为2.7182
toc  %计算tic和toc中间部分的代码的运行时间

2.游戏

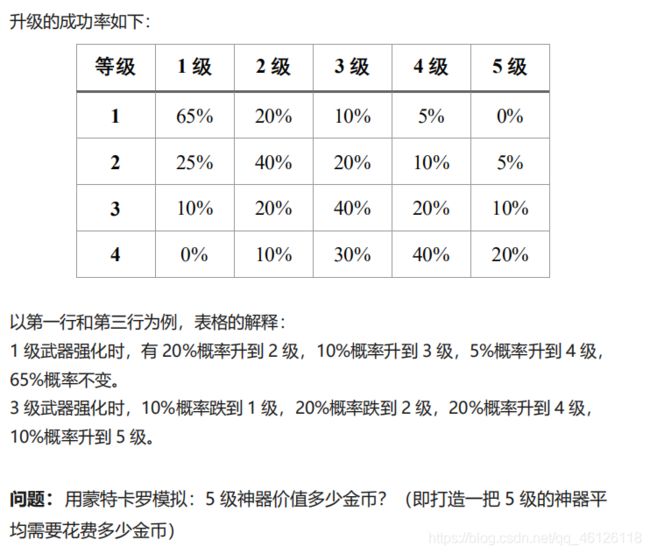
%%  蒙特卡罗解决武器升级问题
% 现在有一把神器，初始为1级，可免费领取（即价值为0），可花费金币对其升级，每次10000金币，最多升到5级。
% 给定一个升级的概率表(见讲义)，问：5级神器价值多少金币？（即升级到5级神器平均的花费）

%% （1）预备知识
% 以一定的概率产生随机数  randsrc(m,n,[alphabet; prob])
% m和n表示生成的随机数矩阵的行数和列数
% alphabet表示需要产生的随机数的数字，用一个行向量表示
% prob表示这些数字出现的概率大小，用一个行向量表示，向量长度和alphabet向量要完全相同, 且这些概率的和要为1
% 比如：要产生1、4、 6这三个数。它们分别出现的概率为 0.1、0.2、0.7，如何设计程序使得按照这个概率产生10个随机数呢？
alphabet = [1 4 6]; prob = [0.1 0.2 0.7];
randsrc(10,1,[alphabet; prob])

%% （2）参考答案
clear;clc
tic  %计算tic和toc中间部分的代码的运行时间
% 升级的成功率储存在success矩阵中，以第一行和第三行为例，表格的解释：
%  1级武器强化时，有20%概率升到2级，10%概率升到3级，5%概率升到4级，65%概率不变。
%  3级武器强化时，10%概率跌到1级，20%概率跌到2级，20%概率升到4级，10%概率升到5级
success = [0.65 0.2  0.1  0.05  0;
                 0.25 0.4  0.2  0.1    0.05;
                 0.1   0.2  0.4  0.2    0.1;
                 0      0.1  0.3  0.4    0.2] ;
n = 10000;  % 蒙特卡罗模拟的次数
MONEY = zeros(n,1);  % 初始化用来存储每次蒙特卡罗计算出来的表示强化费用的向量
for i = 1:n
    rank = 1; % 武器的初始等级
    money = 0;  %花费的钱数，初始化为0
    alphabet = [1 2 3 4 5];   % 用来表示五个等级
    while rank ~= 5  % 只要等级不是5级， 就一直循环下去
        prob =success(rank,:);    % 令生成随机数的概率为第rank行
        rank = randsrc(1,1,[alphabet; prob]);   % 生成一个在1-5中的随机数，表示强化后的等级
        money = money + 10000;  % 更新强化的费用
    end
    MONEY(i) = money;  % 将这次蒙特卡罗的结果保存到MONEY向量中
end
disp(['将武器升级到5级的平均花费为：',num2str(mean(MONEY))])
toc  %计算tic和toc中间部分的代码的运行时间

3.求解非线性问题

%%  蒙特卡罗求解非线性规划问题
% min f(x) =2*(x1^2)+x2^2-x1*x2-8*x1-3*x2
% s.t.
% (1) 3*x1+x2>9
% (2) x1+2*x2<16
% (3) x1>0 & x2>0

%% （1）初次寻找最小值的代码
clc,clear;
format long g   %可以将Matlab的计算结果显示为一般的长数字格式（默认会保留四位小数，或使用科学计数法）
tic %计算tic和toc中间部分的代码的运行时间
n=10000000; %生成的随机数组数
x1=unifrnd(0,16,n,1);  % 生成在[0,16]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=unifrnd(0,8,n,1);  % 生成在[0,8]之间均匀分布的随机数组成的n行1列的向量构成x2
fmin=+inf; % 初始化函数f的最小值为正无穷（后续只要找到一个比它小的我们就对其更新）
for i=1:n
    x = [x1(i), x2(i)];  %构造x向量, 这里千万别写成了：x =[x1, x2]
    if (3*x(1)+x(2)>9)  &  (x(1)+2*x(2)<16)     % 判断是否满足条件
        result = 2*(x(1)^2)+x(2)^2-x(1)*x(2)-8*x(1)-3*x(2);  % 如果满足条件就计算函数值
        if  result  < fmin  % 如果这个函数值小于我们之前计算出来的最小值
            fmin = result;  % 那么就更新这个函数值为新的最小值
            X = x;  % 并且将此时的x1 x2 保存到相应的变量中
        end
    end
end
disp(strcat('蒙特卡罗模拟得到的最小值为',num2str(fmin)))
disp('最小值处x1 x2的取值为：')
disp(X)
toc %计算tic和toc中间部分的代码的运行时间

4.解决实际问题

%% 选择决策方案的模拟
% 某设备上安装有四只型号规格完全相同的电子管，已知电子管寿命为1000--2000小时之间的均匀分布(假定为整数)。
% 当电子管损坏时有两种维修方案，一是每次更换损坏的那一只；二是当其中一只损坏时四只同时更换。
% 已知更换时间为换一只时需1小时，4只同时换为2小时。
% 更换时机器因停止运转每小时的损失为20元，又每只电子管价格10元，
% 试用模拟方法决定哪一个方案经济合理？

%% （1）预备知识
% randi([a,b],m,n)  随机生成m*n的矩阵，矩阵中的每个元素都是[a,b]中的随机整数
randi([1, 5],3,2)
randi([1, 5])  % 不写m*n代表只生成1个随机数

% find函数的用法
% find函数的用法在第一期视频：层次分析法那一节讲过，我们当时找最大特征值的位置
a = [2 3 5 1 7 5];
find(a)  % 找到a中所有非0元素的位置
find(a == 5)  % 找到a中等于5的元素的位置
find(a == 5,1)  % 找到a中第一个等于5的元素的位置
find(a == min(a))   % 找到a中最小元素的位置

%% （2）代码部分
clear;clc
T = 100000000;   % T表示模拟的总时间（单位为小时）
t = 0;   % 初始化当前时刻为0小时
c1 = 0; c2 = 0;  % 初始化两种方案的总花费都为0

%%  方案一
life = randi([1000,2000],1,4);  % 随机生成四个电子管的寿命，假设为整数
while t < T  % 只要现在的时刻没有超过总时刻，就不断循环下去
    result = min(life);  % 找出寿命最短的那一个电子管的寿命
    t = t+result+1;  % 现在的时间更改到有电子管损坏的时刻（加上1表示更换电子管需要花费的时间）
    c1 = c1 + 20 * 1 +10;  % 更新方案一的花费 
    k = find(life == result,1);   % 找到哪一个电子管是坏的
    life = life - result -1; % 更新所有电子管的寿命（这里不减去1也是可以的，减少了1也无所谓，对结果的影响很小）    
    life(k) = randi([1000,2000]);  % 把坏掉的那个电子管的寿命重置
end

%%  方案二
t = 0;   % 初始化当前时刻为0小时
while t < T  % 只要现在的时刻没有超过总时刻，就不断循环下去
    life = randi([1000,2000],1,4); % 随机生成四个电子管的寿命，假设为整数
    result = min(life); % 找出寿命最小的那一个电子管的寿命
    t = t+result+2;  % 现在的时间更改到有电子管损坏的时刻（加上2表示更换所有电子管需要花费的时间）
    c2 =c2 + 20 * 2 +40;  % 更新方案二的花费 
end

%% 两种方案的花费
c1
c2

三.数学规划模型