数据结构之二叉堆
1. 堆（Heap）
也是一种树状的数据结构。
任意节点的值总是大于等于子节点的值，称为最大堆、大根堆、大顶堆。
任意节点的值总是小于等于子节点的值，称为最小堆、小根堆、小顶堆。
堆中的元素必须具备可比较性。
1.1 接口设计
/**
* @Description 堆接口
* @date 2022/4/29 8:52
*/
public interface Heap<E> {
/**
* 元素数量
* @return
*/
int size();
/**
* 是否为空
* @return
*/
boolean isEmpty();
/**
* 清空堆
*/
void clear();
/**
* 添加元素
* @param e
*/
void add(E e);
/**
* 获取堆顶元素
* @return
*/
E get();
/**
* 删除堆顶元素
* @return
*/
E remove();
/**
* 删除堆顶元素的同时插入一个新元素
* @param e
* @return
*/
E replace(E e);
}
2. 二叉堆（Binary Heap）
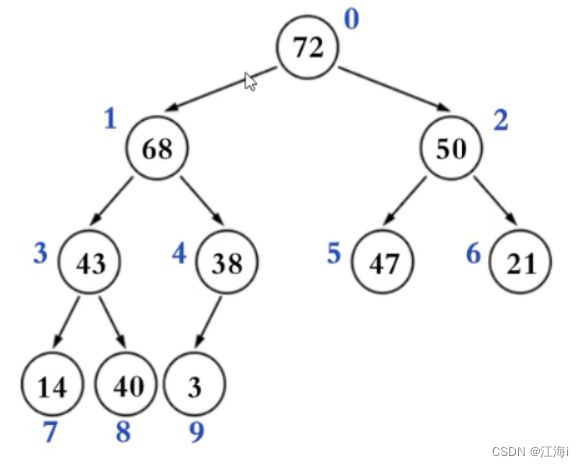
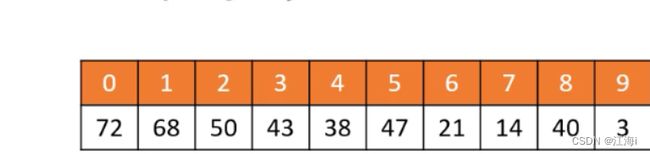
二叉堆的逻辑结构就是一颗完全二叉树，也称完全二叉堆。
使用数组从上到下，从左到右来存储元素。
索引 i 规律（n为元素数量）：
i = 0，根节点；i > 0，则父节点为floor((i - 1) / 2)；2i + 1 <= n - 1，则左子节点为2i + 1；2i + 1 > n - 1，无左子节点；2i + 2 <= n -1，则右子节点为2i + 2;2i + 2 > n - 1，无右子节点。
2.1 二叉堆实现
2.2 全局变量和构造函数
// 存储元素的数组
private E[] es;
// 元素数量
private int size;
// 比较器
private Comparator<E> comparator;
// 默认容量
private static final int DEFAULT_CAPACITY = 10;
public BinaryHeap(Comparator<E> comparator){
this.comparator = comparator;
this.es = (E[]) new Object[DEFAULT_CAPACITY];
}
public BinaryHeap(){
this(null);
}
2.3 比较方法
/**
* 元素比较
* @param e
* @param e1
* @return
*/
private int compare(E e, E e1){
return comparator != null ? comparator.compare(e,e1)
: ((Comparable)e).compareTo(e1);
}
2.4 简单方法实现
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void clear() {
for (E e : es) {
e = null;
}
size = 0;
}
2.5 get()
/**
* 空堆检测
*/
private void emptyCheck(){
if (size == 0){
throw new IndexOutOfBoundsException("Heap is empty");
}
}
@Override
public E get() {
emptyCheck();
return es[0];
}
2.6 add()
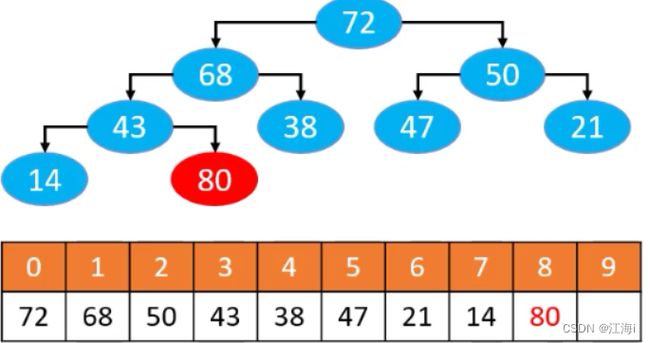
最大堆
- 例如添加元素80，放到数组的最后面，明显逻辑结构不满住大顶堆的性质。
- 解决方法：与父节点交换位置直到不能再往上交换，或者小于父节点。这种方法称为上滤。
/**
* 上滤
* @param index
*/
private void siftUp(int index){
E e = es[index];
while (index > 0){
int parentIndex = (index - 1) >> 1;
E parent = es[parentIndex];
if (compare(e,parent) < 0){
return;
}
// 将父元素放到index位置；
es[index] = parent;
// 将index变为父节点的索引值
index = parentIndex;
}
// 将新节点放到父节点位置
es[index] = e;
}
- 空值检测和扩容
/**
* 空 e 检测
* @param e
*/
private void elementNotNullCheck(E e){
if (e == null){
throw new IllegalArgumentException("E must be not null");
}
}
/**
* 保证要有capacity的容量
* @param capacity
*/
private void ensureCapacity(int capacity) {
int oldCapacity = es.length;
if (oldCapacity >= capacity){
return;
}
// 变成原先容量的 1.5 倍
int newCapacity = oldCapacity + (oldCapacity >> 1);
E[] newElements = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newElements[i] = es[i];
}
es = newElements;
}
- 添加
@Override
public void add(E e) {
elementNotNullCheck(e);
ensureCapacity(size + 1);
es[size++] = e;
siftUp(size - 1);
}
2.7 remove()
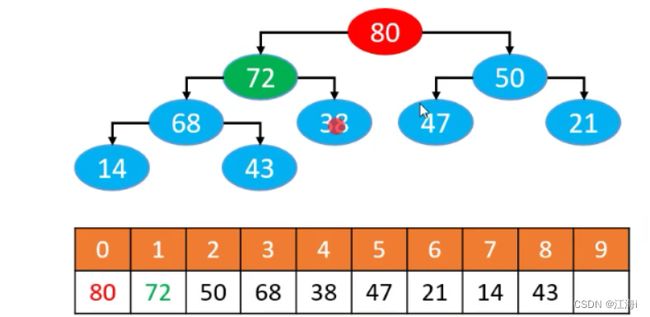
最大堆
直接让最后一个元素替换掉当前堆顶元素：
与子节点中最大的进行交换，直到大于子节点或者无法再进行交换，即可符合最大堆。
这个过程称为下滤。
/**
* 下滤
* @param index
*/
private void siftDown(int index){
E e = es[index];
// 计算出非叶子节点数量
int half = size >> 1;
while (index < half){
// 因为可能没有右子节点，默认使用右子节点
int childIndex = (index << 1) + 1;
// 获取右子节点
int rightIndex = childIndex + 1;
if (rightIndex < size && compare(es[childIndex],es[rightIndex]) < 0){
childIndex = rightIndex;
}
E child = es[childIndex];
if (compare(e,child) >= 0){
break;
}
es[index] = child;
index = childIndex;
}
es[index] = e;
}
@Override
public E remove() {
emptyCheck();
int lastIndex = --size;
E root = es[0];
es[0] = es[lastIndex];
es[lastIndex] = null;
siftDown(0);
return root;
}
2.8 replace()
public E replace(E e) {
elementNotNullCheck(e);
E root = es[0];
if (size == 0){
es[0] = e;
size = 1;
}else {
// 替换堆顶
es[0] = e;
siftDown(0);
}
return root;
}
2.9 最大堆-批量建堆
给定一组数据，创建一个堆，如果
for循环add()消耗内存比较高。
2.9.1 自上而下的上滤
从索引为1的元素开始，如果大于父节点就与父节点交换位置，直到全部交换完毕，符合最大堆
但是这个效率基本等同于添加的效率：底层的元素不仅数量多而且比较的次数也多。时间复杂度为O(nlogn)
2.9.2 自下而上的下滤
从最后一个索引位置的元素开始，排除叶子节点，如果小于子节点就与子节点交换位置。
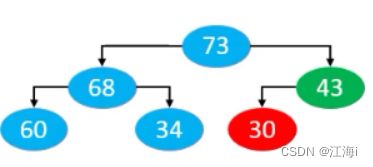
明显的可以看出，下滤的效率高于上滤的效率：只有最上层的元素需要全部进行比较（符合条件的前提下）。时间复杂度为O(n)。
2.9.3 实现
- 构造函数
public BinaryHeap(){
this(null,null);
}
public BinaryHeap(E[] es, Comparator<E> comparator){
if (es == null || es.length == 0){
this.es = (E[]) new Object[DEFAULT_CAPACITY];
}else {
size = es.length;
int capacity = Math.max(es.length,DEFAULT_CAPACITY);
this.es = (E[]) new Object[capacity];
for (int i = 0; i < es.length; i++) {
this.es[i] = es[i];
}
heapify();
}
this.comparator = comparator;
}
public BinaryHeap(E[] es){
this(es,null);
}
- 批量创建
/**
* 批量创堆
*/
private void heapify(){
// // 自上而下的上滤
// for (int i = 1; i < size; i++) {
// siftUp(i);
// }
// 自下而上的下滤
for (int i = (size >> 1) - 1 ; i >= 0; i--) {
siftDown(i);
}
}
2.10 小顶堆
只需要在创建堆的时候指定相反的比较策略即可。
private static void test3(){
Integer[] integers = {72,68,43,38,14,10,3,50,47,21};
BinaryHeap<Integer> heap = new BinaryHeap<>(integers, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
BinaryTrees.println(heap);
}
3. Top K 问题
在n个整数中，找到最大（小）的 k 个数。
- 最小的前 n 个数，使用大顶堆
/**
* 获取最小的前 k 个元素
* @param nums
* @param k
*/
public static void getTopMinK(Integer[] nums, int k){
BinaryHeap<Integer> heap = new BinaryHeap<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
for (int i = 0; i < nums.length; i++) {
if (heap.size() < k){
heap.add(nums[i]);
}else {
if (nums[i] < heap.get()){ // 如果当前元素小于堆顶元素，则加入到堆中。
heap.replace(nums[i]);
}
}
}
}
- 最大的前 n 个数，使用小顶堆
/**
* 获取最大的前 k 个元素
* @param nums
* @param k
*/
public static void getTopMaxK(Integer[] nums, int k){
BinaryHeap<Integer> heap = new BinaryHeap<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
for (int i = 0; i < nums.length; i++) {
if (heap.size() < k){
heap.add(nums[i]);
}else {
if (nums[i] > heap.get()){ // 如果当前元素大于堆顶元素，则加入到堆中。
heap.replace(nums[i]);
}
}
}
}