【蓝桥杯】第十三届蓝桥杯真题 AK 攻略 —— C++ B组全真题超详细剖析
目录
- 写在前面
-
- A题 --- 九进制转十进制
-
- 题目描述
- 解题思路
- 代码编写
- B题 --- 顺子日期
-
- 题目描述
- 解题思路
- 代码编写
- C题 --- 刷题统计
-
- 题目描述
- 解题思路
- 代码编写
- D题: 修剪灌木
-
- 题目描述
- 解题思路
- 代码编写
- E题:X进制减法
-
- 题目描述
- 解题思路
- 代码编写
- F题:统计子矩阵
-
- 题目描述
- 解题思路
- 代码编写
- G题:积木画
-
- 题目描述
- 解题思路
- 代码编写
- H题:扫雷
-
- 题目描述
- 解题思路
- 代码编写
- I题:李白打酒加强版
-
- 题目描述
- 解题思路
- 代码编写
- J题:砍竹子
-
- 题目描述
- 解题思路
- 代码编写
- 写在最后
写在前面
Hello朋友们,我是秋刀鱼,一只活跃于Java区与算法区的新人博主~
欢迎大家加入高校算法学习社区, 社区里大佬云集,大家互相交流学习!
蓝桥杯的成绩已经公布,看到很多朋友拿了奖秋刀鱼很是高兴!大家都是好样的!因为疫情缘故秋刀鱼的蓝桥杯比赛被推迟到了 5 月 14 日第二批,因此还有半个月的时间进行准备。今天呢给大家带来蓝桥杯 C++ B组真题解析,这套题目也是耗费了我将近 7 个小时的时间才AK,希望看完能让你有所收获。如果觉得博主写的还不错的话务必三连支持一下:
主页:秋刀鱼与猫期待你的支持与关注~
A题 — 九进制转十进制
题目描述
解题思路
很简单一道进制转换题目!这可不能做错哦!
代码编写
#include#include using namespace std; int main() { cout << 2 * pow(9, 0) + 2 * pow(9, 1) + 0 * pow(9, 2) + 2 * pow(9, 3) << endl; return 0; }
B题 — 顺子日期
题目描述
解题思路
这道题实现起来还算简单,但是题目中的说明有点模棱两可,
012到底能不能作为顺子呢?最后官方说明两个答案都算正确。
代码编写
#include#include #include using namespace std; const int months[] = { 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 }; bool check(string str) { for (int i = 0; i + 2 < str.size(); i ++ ) if (str[i + 1] == str[i] + 1 && str[i + 2] == str[i] + 2) return true; return false; } int main() { int year = 2022, month = 1, day = 1; int res = 0; for (int i = 0; i < 365; i ++ ) { char str[10]; sprintf(str, "%04d%02d%02d", year, month, day); if (check(str)) { res ++ ; cout << str << endl; } if ( ++ day > months[month]) { day = 1; month ++ ; } } cout << res << endl; return 0; }
C题 — 刷题统计
题目描述
题传送门
解题思路
计算出从周一开始刷题一周的刷题数量 w e e k C o s t weekCost weekCost ,将 n / w e e k C o s t n/weekCost n/weekCost 获取到需要多少个周,更新答案。获取剩余的题目,剩余的题目一定能在一周之内完成,继续枚举获取答案值。非常简单!
代码编写
#include#define ll long long using namespace std; int main() { ll a, b, n; cin >> a >> b >> n; ll weekCost = a * 5 + b * 2; ll ans = 0; ans += (n / weekCost) * 7; n %= weekCost; for (int i = 1; n > 0 && i <= 7; ++i,++ans) { if (i <= 5) { n -= a; } else { n -= b; } } cout << ans; return 0; }
D题: 修剪灌木
题目描述
题目传送门
解题思路
解决本题的关键是判断每棵灌木最高的高度,简单地思考不难发现该高度与该点距离左、右侧边界的距离相关。定义左侧边界距离为 i i i ,则右侧边界可计算出为: n − i − 1 n-i-1 n−i−1,如下图所示:
灌木的最高高度就是: m a x { i , n − i − 1 } ∗ 2 max\{i,n-i-1\} * 2 max{i,n−i−1}∗2
代码编写
#include#include #define ll long long using namespace std; int main() { int n; cin >> n; for (int i = 0; i < n; ++i) { cout << max(i , (n - i - 1)) * 2; cout << endl; } return 0; }
E题:X进制减法
题目描述
题目传送门
解题思路
理解题意
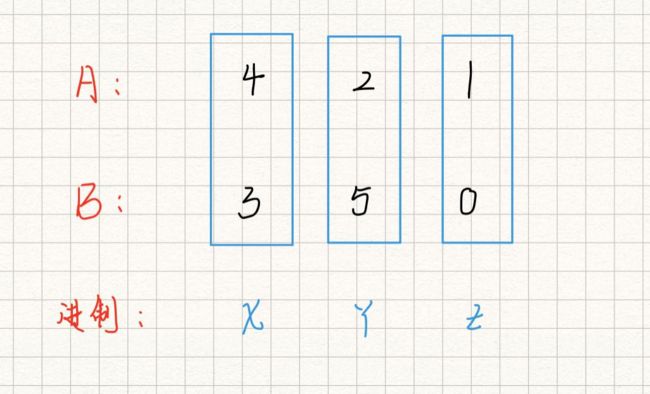
我相信很多朋友不会做这道题是因为题目的意思没有理清楚。其实题目的要求很简单:给定了两个整数 A,B,这两个数每一位上可以是任意进制,但是A,B相同位上进制规则相同。举个栗子:
若 X,Y,Z 分别代表 5,6,2 进制,则 A = 4*6*2 + 2*6 + 1 ,B = 3*6*2 + 5*6 + 0
如 X,Y,Z 分别代表 6,7,3 进制,则 A = 4*7*3 + 2*7 + 1 ,B = 3*7*3 + 5*7 + 0
无论每一位进制为何值,都需要满足:
- 进制数要大于改位的最大值
- 进制数的最小值为 2
满足上述要求的每一位进制所得到的数:A,B ,题目要求获取 A - B 的最小值。
解题方法
首先给出结论:只需要将每一位进制数设置为最小值, A - B 的值一定是最小值。
结论证明
首先假设 A 的每一位值为 A i A_i Ai,最低位的值为 A 1 A_1 A1 ,最高位的值为 A n A_n An ,B 同理。同时假设每一位的进制为 S i S_i Si 最低位进制为 S 1 S_1 S1 ,最高位进制为 S n S_n Sn。下面以 n = 4 为例进行证明:
经过推导不难发现 A-B 的值能进行如下的表示:
先考虑箭头所指位置:题目中给定了 A − B > 0 A - B >0 A−B>0 ,因此 A 4 − B 4 > = 0 A_4 - B_4 >= 0 A4−B4>=0 恒成立, 为了使结果值最小,因此 S 3 S_3 S3 的值应当最小。
继续看箭头所指的位置,因为 S 3 S_3 S3 是第三位的进制数,因此 S 3 > A 3 S_3 > A_3 S3>A3且 S 3 > B 3 S_3 > B3 S3>B3 ,而 A 4 − B 4 > = 0 A_4 - B_4 >=0 A4−B4>=0,因此 S 3 ( A 4 − B 4 ) > = ( A 3 − B 3 ) S_3(A_4-B_4) >= (A_3-B_3) S3(A4−B4)>=(A3−B3),因此方框位置的值仍为正数或 0 ,为了使该值最小, S 2 S_2 S2 应当取最小值。
继续证明的思路与上述思路相同,通过证明最终得出:为了使 A − B A-B A−B 的值最小,每一位的表示的进制数应当最小!
代码编写
#includeF题:统计子矩阵
题目描述
题目传送门
【评测用例规模与约定】
对于 30% 的数据,N, M ≤ 20.
对于 70% 的数据,N, M ≤ 100.
对于 100% 的数据,1 ≤ N, M ≤ 500; 0 ≤ *Ai j* ≤ 1000; 1 ≤ K ≤ 250000000**
解题思路
二维前缀和
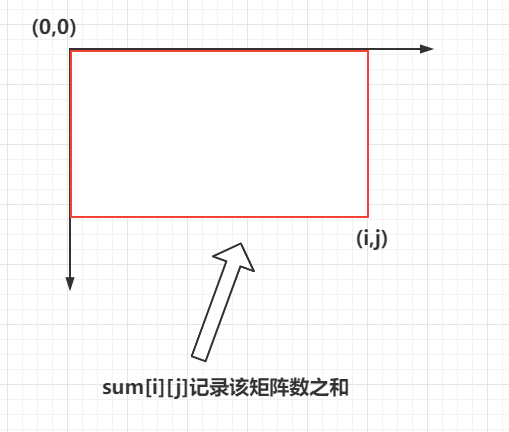
对于任意一个矩阵,如何快速获取到任意一个字矩阵中所有数的和呢?可以使用二维前缀和的思想。定义一个二维前缀和数组 s u m [ n ] [ m ] sum[n][m] sum[n][m] 记录前缀和, s u m [ i ] [ j ] sum[i][j] sum[i][j] 记录 ( 0 , 0 ) − > ( i , j ) (0,0) -> (i,j) (0,0)−>(i,j) 矩阵中的数之和,就如下图所示:
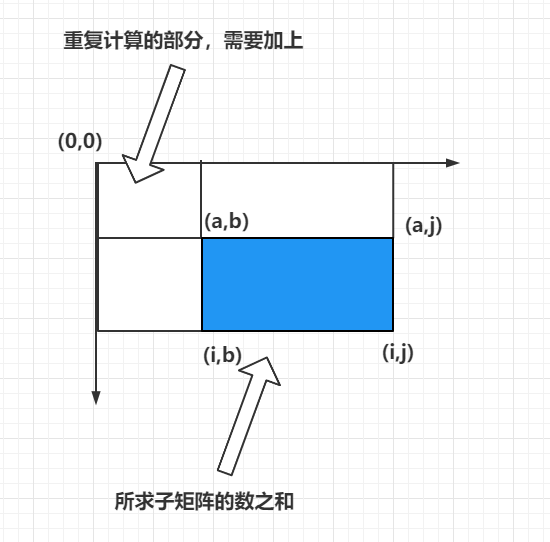
获取任意一个子矩阵 ( a , b ) − > ( i , j ) (a,b) - >(i,j) (a,b)−>(i,j) 矩阵数之和等于 : s u m [ i ] [ j ] − s u m [ a − 1 ] [ j ] − s u m [ i ] [ b − 1 ] + s u m [ a − 1 ] [ b − 1 ] sum[i][j] - sum[a-1][j] - sum[i][b-1] + sum[a-1][b-1] sum[i][j]−sum[a−1][j]−sum[i][b−1]+sum[a−1][b−1] 如下图所示:
只需要预先处理好前缀和数组,按照上述方式就能够在 O ( 1 ) O(1) O(1)的时间复杂度下求出任意子矩阵的数之和。
二分查找
不妨我们将遍历每一个点,将遍历到的点作为矩阵左上侧的点固定。同时遍历剩余的点,遍历得到右下侧的点通过这两个点确定一个矩形,再根据二维前缀和得到该矩形数之和即可获得答案,但是这样的时间复杂度是 O ( N 4 ) O(N^4) O(N4)对于 500 的数据量可能会超时,有什么更好的方法呢?
其实使用二分就可以解决上面的问题,具体操作如下:
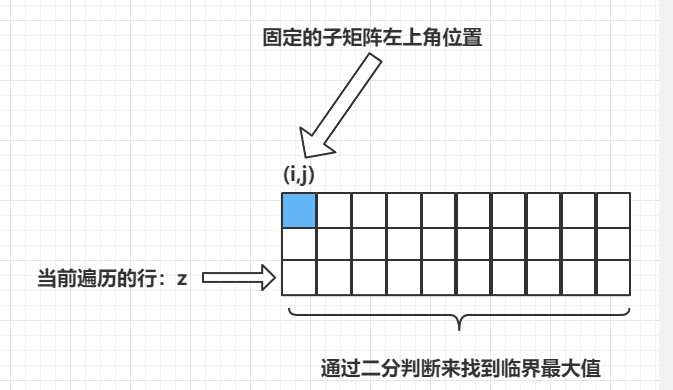
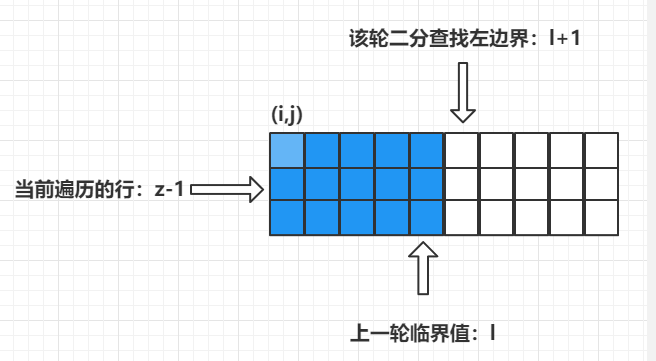
固定了左上角点后遍历每一行时,因为从左到右遍历生成的子矩阵其数之和一定是递增的(因为拿取了越来越多的数),因此只需要对每一行的数据使用二分查找该行形成的子矩阵的数据,找到临界值点即可,如下图所示:
满足: ( i , j ) − > ( z , l ) (i,j) ->(z,l) (i,j)−>(z,l) 矩阵数之和小于等于 K,而对于 ( i , j ) − > ( z , l + 1 ) (i,j)->(z,l+1) (i,j)−>(z,l+1) 矩阵数之和一定大于 K,因此能够通过二分查找的方式查找搜索每一行来找到该临界值 l l l ,此时可以获得的子矩阵数量为 l − j + 1 l-j+1 l−j+1,可以将时间复杂度优化为 O ( N 3 ⋅ l g N ) O(N^3\cdot lgN) O(N3⋅lgN)。
继续优化
虽然说上述的方法已经能够极大地降低时间复杂度,但是还是无情地超时了:
还需要进一步的优化:
还是上述的解法,只不过固定左上角点 ( i , j ) (i,j) (i,j) 后枚举每一行时,按照 z 下标从大到小的方式枚举:
还是上述的情况,在 z z z 行枚举到 l l l 值之后,不难发现蓝色区域内以 ( i , j ) (i,j) (i,j)作为左上角点的子矩阵数量是能够计算出来的,该值就是蓝色区域内的方块数目 ( l − j + 1 ) ⋅ ( z − i + 1 ) (l-j+1)\cdot (z-i+1) (l−j+1)⋅(z−i+1) ,直接将该值更新到答案中。按照下标从大到小的顺序遍历因此下一次遍历的行是 z − 1 z-1 z−1 行,因为蓝色区域中包含了 z − 1 z-1 z−1 行的一部分,而这一部分已经被更新到了答案之中。因此该二分查找的范围有所变化,二分查找的左边界只需要定为 l + 1 l+1 l+1 ,如下图所示:
这样通过压缩二分查找的左边界范围而减少二分查找次数,最终 AC 这道题。
代码编写
#include G题:积木画
题目描述
题传送门
写在前面
这道题我有在网上去搜索了一下其他博主的题解,因为我实在无法理解 d p [ i ] = d p [ i − 1 ] ⋅ 2 + d p [ i − 3 ] dp[i] = dp[i-1]\cdot2+dp[i-3] dp[i]=dp[i−1]⋅2+dp[i−3] 这个状态转移方程是如何得到的(可能是自己太笨了),他们的题解大多都是草草两句收尾讲的有些含糊不清,作为菜狗的我真的很难懂啊啊啊啊!在思考良久后对于这道题我想到了一种自己的解题想法,与网上主流的状态转移方程不同不过同样能够解题。
解题思路
状态表示
本题解题的关键是使用动态规划,定义一维数组 d p dp dp , d p [ i ] dp[i] dp[i] 存储画布的大小为 2 × i 2\times i 2×i 时积木的填充方法数。
状态初始化
不难发现:
- 当画布大小为 2 × 1 2\times 1 2×1 时,只能放下一个 I 型积木,因此 d p [ 1 ] = 1 dp[1] =1 dp[1]=1。
情况梳理
梳理状态转移方程之前,不妨思考下,积木画出现在最后且符合题意的积木块只能出现哪几种情况呢?
状态转移方程
情况一:单独使用 I 型积木拼接, d p [ i ] + = d p [ i − 1 ] dp[i] += dp[i-1] dp[i]+=dp[i−1]
情况二:使用两个 I 型积木拼接, d p [ i ] + = d p [ i − 2 ] dp[i]+=dp[i-2] dp[i]+=dp[i−2]
情况三:使用两个 L 型积木拼接, d p [ i ] + = 2 ⋅ d p [ i − 3 ] dp[i]+=2\cdot dp[i-3] dp[i]+=2⋅dp[i−3]
情况四:情况四只有 i > = 4 i>=4 i>=4 时才可能出现,具体讨论如下:
- 若 i = = 4 i==4 i==4 ,只存在长度为 4 的拼接情况,假设 d p [ 0 ] = 1 dp[0]=1 dp[0]=1,也就是说 d p [ 4 ] + = d p [ 0 ] ⋅ 2 dp[4]+=dp[0]\cdot 2 dp[4]+=dp[0]⋅2
- 若 i = = 5 i==5 i==5,存在长度为 4 , 5 4,5 4,5 的拼接情况,即 d p [ 5 ] + = ( d p [ 0 ] + d p [ 1 ] ) ⋅ 2 dp[5] += (dp[0]+dp[1])\cdot 2 dp[5]+=(dp[0]+dp[1])⋅2
- 若 i = = 6 i ==6 i==6,继续推导有: d p [ 6 ] + = ( d p [ 0 ] + d p [ 1 ] + d p [ 2 ] ) ⋅ 2 dp[6]+=(dp[0]+dp[1]+dp[2])\cdot 2 dp[6]+=(dp[0]+dp[1]+dp[2])⋅2
- 若 i = = 7 i==7 i==7,推导有: d p [ 7 ] + = ( d p [ 0 ] + d p [ 1 ] + d p [ 2 ] + d p [ 3 ] ) ⋅ 2 dp[7]+=(dp[0]+dp[1]+dp[2]+dp[3])\cdot 2 dp[7]+=(dp[0]+dp[1]+dp[2]+dp[3])⋅2
按照上述推导,不难发现 d p [ i ] + = ( d p [ 0 , 1 , 2 , . . . , i − 4 ] ) ⋅ 2 dp[i]+=(dp[0,1,2,...,i-4])\cdot 2 dp[i]+=(dp[0,1,2,...,i−4])⋅2,因此可以定义一个变量 s u m sum sum 存储 d p [ 0 , 1 , 2 , . . i ] dp[0,1,2,..i] dp[0,1,2,..i] 的值,在 i i i 增大的同时更新 s u m sum sum 的值,初始情况 s u m = 0 sum=0 sum=0。
返回结果
最终 d p [ N ] dp[N] dp[N] 就是题目所求值,这道题就这样解决了。需要注意:下面代码中仅使用 a 1 , a 2 , a 3 a1,a2,a3 a1,a2,a3 分别代表 d p [ i − 1 ] , d p [ i − 2 ] , d p [ i − 3 ] dp[i-1],dp[i-2],dp[i-3] dp[i−1],dp[i−2],dp[i−3]。
代码编写
#include#include #define ll long long // #include using namespace std; const int MOD = 1000000007; int main() { ll n, a1, a2, a3; a1 = 5; a2 = 2; a3 = 1; cin >> n; ll sum = 0; for (ll i = 4; i <= n; ++i) { ll val = 0; val += a1; val += a2; val += (a3 * 2L); if (i >= 4) { val += sum * 2 + 2; sum += a3; } val %= MOD; a3 = a2; a2 = a1; a1 = val; } cout << a1; return 0; }
H题:扫雷
题目描述
题传送门
写在前面
个人觉得本题是第十三届蓝桥杯 C++ B组最难的一道题目,常规思路最多能骗骗分,如果需要AC本道题目需要使用特殊的优化。因此整体难度偏高。
解题思路
核心思路
我的解题思路是搜索算法 + 哈希散列,如果直接使用BFS、DFS算法搜索可能会导致超时,这里我将每一个二维的坐标通过哈希值散列为一维数组的一个索引值,缩短搜索的时间。
哈希散列
如果有学习过Java的朋友可能了解过 HashMap 的底层源码,其核心是根据传入的 Key 计算出其哈希值,并将哈希值通过散列算法散列到桶数组中,并使用链表+红黑树的存储结构解决哈希冲突。
本题中给定了炸雷的坐标 ( x , y ) (x,y) (x,y) ,我们也可以定义一个哈希算法根据 x , y x,y x,y 的值将其转换为哈希值。通过该哈希值就能够判断出 ( x , y ) (x,y) (x,y) 坐标是否出现。因为 x , y x,y x,y 的取值为 [ 0 , 1 0 9 ] [0,10^9] [0,109],因此不难得到下面的哈希算法:
// 获取每个点的哈希值 ll hashCode(int x, int y) { return x * 1e9+100L + y; }现在获取到了哈希值,这是一个非常大的数,如果使用一个数组存储所有哈希值是否出现肯定是不可取的。
这里就需要使用到哈希散列,操作方法:定义一个散列数组 h a s h U s e d hashUsed hashUsed,将哈希值映射到 h a s h U s e d hashUsed hashUsed 一个索引位置。
现在假设发射了一枚排雷火箭,通过遍历所有其爆炸范围内的点 ( x i , y i ) (x_i,y_i) (xi,yi) ,判断其散列到 h a s h U s e d hashUsed hashUsed 数组的索引位是否有值来判断该点是否为炸雷。
哈希冲突
哈希散列不可避免哈希冲突,解决哈希冲突的方式也有很多,这里我使用的是 线性探测法。如果哈希散列索引位置值已经存在,则在原来索引的基础上往后加一个单位,直至不发生哈希冲突。具体实现参考代码注释。
代码编写
#include#include #define ll long long using namespace std; const int N = 5e4, M = 8e6; const ll MAX = 1e9+100; struct point { int x, y, r; }points[N]; // 保存哈希散列情况 ll hashUsed[M]; // 散列值到points下标信息 int id[M]; // 保存炸弹是否被引爆 int used[M]; // 获取每个点的哈希值 ll hashCode(int x, int y) { return x * MAX + y; } int Dist(int x, int y, int i, int j) { return (x - i) * (x - i) + (y - j) * (y - j); } // 哈希散列函数 int getPos(int x, int y) { ll hash = hashCode(x, y); // 散列化哈希code int pos = (hash % M + M) % M; // 解决哈希冲突 while (hashUsed[pos] != -1 && hashUsed[pos] != hash) { // 遇上边界,继续加一会越界,因此将pos循环到0索引位置 if (++pos == M) { pos = 0; } } return pos; } // dfs搜索,(x,y,r)为炸弹信息,bomb 代表该点是否为 炸雷 void dfs(int x, int y, int r, bool bomb) { if(bomb) { used[getPos(x, y)] = 1; } // 遍历爆炸范围内所有的点 for (int i = x - r; i <= x + r; ++i) { for (int j = y - r; j <= y + r; ++j) { if (Dist(x, y, i, j) <= r * r) { int pos = getPos(i, j); // 该位置是一个炸雷且没有被引爆 if (!used[pos] && id[pos]) { dfs(i, j, points[id[pos]].r, true); } } } } } int main() { int n, m, ret; ret = 0; cin.tie(); cin >> n >> m; memset(used, 0, sizeof used); // 初始为 -1 memset(hashUsed, -1, sizeof hashUsed); // 将炸雷散列后存储 for (int i = 1; i <= n; ++i) { int x, y, r; cin >> x >> y >> r; points[i] = { x,y,r }; ll hash = hashCode(x, y); int pos = getPos(x, y); // 散列的位置值为该位置的哈希值 hashUsed[pos] = hash; // 建立对应关系 id[pos] = i; } while (m--) { int x, y, r; cin >> x >> y >> r; dfs(x,y,r,false); } for (int i = 1; i <= n; ++i) { int pos = getPos(points[i].x, points[i].y); // 该位置的炸雷被引爆 if (used[pos]) { ++ret; } } cout << ret; return 0; }
I题:李白打酒加强版
题目描述
题传送门
解题思路
状态表示
本题的解题核心是动态规划,定义三维数组 d p dp dp 存储状态, d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k] 表示路上遇到了 i i i 次店, j j j 次花后,酒壶中酒剩余 k k k 斗的方法数。
状态初始化
初始情况李白没有遇到店、花,初始状态下酒壶中有 2 斗,因此定义 d p [ 0 ] [ 0 ] [ 2 ] = 1 dp[0][0][2]=1 dp[0][0][2]=1 为初始状态。
状态转移
- 如果当前状态遇到一次店,即 i > 0 i>0 i>0 且 剩余酒的数量应该是之前的两倍,即 k % 2 = = 0 k\%2==0 k%2==0 ,此时 d p [ i ] [ j ] [ k ] + = d p [ i − 1 ] [ j ] [ k / 2 ] dp[i][j][k]+=dp[i-1][j][k/2] dp[i][j][k]+=dp[i−1][j][k/2]
- 如果当前状态遇到一次花,即 j > 0 j>0 j>0,此时 d p [ i ] [ j ] [ k ] + = d p [ i ] [ j − 1 ] [ k + 1 ] dp[i][j][k]+=dp[i][j-1][k+1] dp[i][j][k]+=dp[i][j−1][k+1],k+1 表示酒被喝掉了一斗。
返回结果
因为最后一次遇到的一定是花且剩余酒的数量为 0 ,不妨将状态转换为:共遇到 n n n 次店, m − 1 m-1 m−1 次花且剩余酒的数量为 1,这样返回 d p [ n ] [ m − 1 ] [ 1 ] dp[n][m-1][1] dp[n][m−1][1] 就是题目所求。轻松拿下!
代码编写
#include#include #define ll long long const int M = 110; ll dp[M][M][M]; const int mod = 1000000007; using namespace std; int main(){ // 0 表示花 1 表示店 memset(dp, 0, sizeof dp); dp[0][0][2] = 1; int n, m; cin >> n >> m; for (int i = 0; i <= n; ++i) { for (int j = 0; j <= m; ++j) { for (int k = 0; k <= 101; ++k) { if (i == 0 && j == 0) { continue; } else { // 店 if (i > 0 && !(k & 1)) { dp[i][j][k] += dp[i - 1][j][k / 2]; } // 花 if (j > 0) { dp[i][j][k] += dp[i][j - 1][k + 1]; } dp[i][j][k] %= mod; } } } } cout << dp[n][m - 1][1]; return 0; }
J题:砍竹子
题目描述
题传送门
解题思路
解题思路
本题的解法有很多,这里我使用的是优先队列 + 区间合并来解决。
问题一:为什么使用优先队列呢?
可以这样思考,魔法只能够作用于相同高度连续的一段竹子上。也就是说对于最高的那一段竹子无法被作用于剩余竹子的魔法所干预,因此优先处理最高的一段竹子一定是最优解。这也就是为什么需要使用优先队列,优先队列负责弹出高度最高的那一段区间。
问题二:如何处理区间呢?
魔法只能作用于相同高度且连续的一段竹子上,定义数据结构
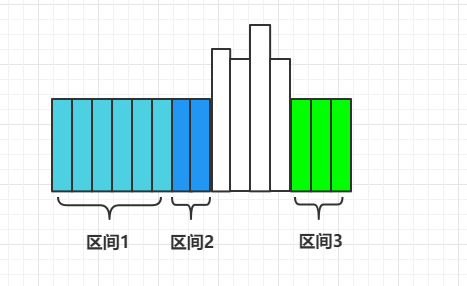
myNode代表一段相同高度且连续的区间,l,r表示区间在的索引范围,val表示这段竹子的高度。既然优先队列弹出最高高度的区间段,很显然该区间段可能不止一个一段,可能是有多段。对于连续的区间段,可以将其拼接为一段区间,就如下图所示:
上图中,区间1与区间2因为区间段连续可以合并,而区间3因为不与区间2连续因此无法合并。
为了能够将所有连续的区间段合并,这就要需要优先队列中,如果区间最高高度相同,则按照区间次序排序。这样就能保证能够合并优先队列中的区间。
代码逻辑
弹出队列中所有最高竹子的区间段,将能够合并的区间段进行合并,最后判断合并后剩余多少个区间段即是需要使用魔法的次数。随后将处理后的高度
c_value修改剩余区间段的最高高度value并将其重新压入队列中。
代码编写
#include#include #include #include #define ll long long using namespace std; // 区间数据结构 class myNode { public : int l, r; ll val; myNode(int l, int r, ll val) { this->l = l; this->r = r; this->val = val; } }; // 自定义排序方式 bool operator < (const myNode& t,const myNode& node) { if (t.val == node.val) { return t.l > node.l; } return t.val < node.val; } int main(){ // 优先队列 priority_queue<myNode>qu; int n; cin >> n; vector<ll>nums; for (int i = 0; i < n; ++i) { ll val; cin >> val; nums.push_back(val); } // 存入区间的初始化状态 for (int i = 0; i < n; ++i) { int l, r; l = r = i; while (r + 1 < n && nums[r + 1] == nums[l]) { ++r; } i = r; if (nums[l] != 1) { qu.push(myNode(l, r, nums[l])); } } int t = 0; while (!qu.empty()) { myNode top = qu.top(); int left = top.l; int right = top.r; ll value = top.val; // 被魔法处理后的区间高度 ll c_value = sqrt(value / 2 + 1); qu.pop(); // 合并区间 while (!qu.empty() && qu.top().val == value) { myNode tmp = qu.top(); int l = tmp.l; int r = tmp.r; qu.pop(); // 能够区间合并 if (l == right + 1) { right = r; } // 无法区间合并 else { if (c_value != 1) { qu.push({ left,right,c_value }); } left = l; right = r; ++t; } } if (c_value != 1) { qu.push({ left,right,c_value }); } ++t; } cout << t; return 0; }
写在最后
总的来说,这次C++ B组的题目考察的知识点没有过分的难,基本上是常考的例如搜索、BFS、DFS、前缀和、二分等等,因此我相信只需要充分准备在赛场上还是能够得心应手。
最后感谢你的观看