蓝桥杯 2020年省赛真题 10月第二场 (Java 大学C组)

---

_Placeholder

---

#A 约数个数

本题总分：$5$ 分

---

问题描述

  对于一个整数，能整除这个整数的数称为这个数的约数。
  例如：$1,2,3,6$ 都是 $6$ 的约数。
  请问 $78120$ 有多少个约数。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

96

---

朴素解法

---

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 78120;

    void run() {
        int ans = 0;
        for (int i = 1; i <= N; i++)
            if (N % i == 0) ans++;
        System.out.println(ans);
    }
}

  蓝桥嘛，会写个 $\mathrm{f}\mathrm{o}\mathrm{r}$ 就能省一。

---

因数个数定理

---

  算是算术基本定理的推论，

  我们知道对于一个大于 $1$ 的自然数 $n$，可以分解为：

  $n=\prod _{i=1}^k{p}_i^{a_i}=p_1^{a_1}\cdot p_2^{a_2}\cdot \cdots \cdot p_k^{a_k}$，

  显然，$n$ 的因数个数为：

  $f(n)=\prod _{i=1}^k(a_i+1)=(a_1+1)(a_2+1)\cdots (a_k+1)$，

  其中 $p_i$ 为质数，$a_i$ 为 $p_i$ 的指数。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 78120;

    void run() {
        int ans = 1;
        for (int p = 2; p * p <= N; p++)
            if (N % p == 0) {
                int a = 1;
                while (N % p == 0) {
                    N /= p;
                    a++;
                }
                ans *= a;
            }
        System.out.println(N == 1 ? ans : ans << 1);
    }
}

---

#B 寻找 2020

本题总分：$5$ 分

---

问题描述

  小蓝有一个数字矩阵，里面只包含数字 $0$ 和 $2$。小蓝很喜欢 $2020$，他想找到这个数字矩阵中有多少个 $2020$。
  小蓝只关注三种构成 $2020$ 的方式：

  1. 同一行里面连续四个字符从左到右构成 $2020$。
  2. 同一列里面连续四个字符从上到下构成 $2020$。
  3. 在一条从左上到右下的斜线上连续四个字符，从左上到右下构成 $2020$。

  例如，对于下面的矩阵：

220000
000000
002202
000000
000022
002020

  一共有 $5$ 个 $2020$。其中 $1$ 个是在同一行里的，$1$ 个是在同一列里的，$3$ 个是斜线上的。
  小蓝的矩阵比上面的矩阵要大，由于太大了，他只好将这个矩阵放在了一个文件里面，在试题目录下有一个文件 2020.txt，里面给出了小蓝的矩阵。
  请帮助小蓝确定在他的矩阵中有多少个 $2020$。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

16520

---

import java.util.*;
import java.io.*;

public class Test {

    public static void main(String[] args) { new Test().run(); }
    
    void run() {
        try (Scanner in = new Scanner(new FileInputStream("2020.txt"))) {
            List<String> lines = new ArrayList();
            while (in.hasNextLine())
                lines.add(in.nextLine());
            int N = lines.size(), M = lines.size() == 0 ? 0 : lines.get(0).length(), ans = 0;
            int[][] offset = {{0, 1}, {1, 0}, {1, 1}};
            char[] target = { '2', '0', '2', '0' };
            for (int i = 0; i < N; i++)
                for (int j = 0; j < M; j++)
                    for (int k = 0; k < 3; k++) {
                        int count = 0;
                        for (int x = i, y = j, s = 0; x < N && y < M && s < 4; x += offset[k][0], y += offset[k][1], s++)
                            if (target[s] == lines.get(x).charAt(y)) count++;
                        if (count == 4) ans++;
                    }
            System.out.println(ans);
        } catch (IOException e) {
            e.printStackTrace();
        }
    }
}

  没啥好说的，

  不想花精力学 $\mathrm{I}\mathrm{O}$ 可以记一下 System.setIn(new FileInputStream(fileName)) 这个方法，

  $\mathrm{C}/\mathrm{C}$++ 的话对应着 freopen(fileName, "r", stdin);，

  当然能掌握最好。

---

#C 跑步锻炼

本题总分：$10$ 分

---

问题描述

  小蓝每天都锻炼身体。
  正常情况下，小蓝每天跑 $1$ 千米。如果某天是周一或者月初（$1$ 日），为了激励自己，小蓝要跑 $2$ 千米。如果同时是周一或月初，小蓝也是跑 $2$ 千米。
  小蓝跑步已经坚持了很长时间，从 $2000$ 年 $1$ 月 $1$ 日周六（含）到 $2020$ 年$10$ 月 $1$ 日周四（含）。请问这段时间小蓝总共跑步多少千米？

---

答案提交

  这是一道结果填空题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

8879

---

Java 8

---

  确实好用了一点。

import java.time.temporal.ChronoUnit;
import java.time.*;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    void run() {
        LocalDate start = LocalDate.of(2000, 1, 1);
        LocalDate end = LocalDate.of(2020, 10, 1);
        long ans = 1 + start.until(end, ChronoUnit.DAYS);
        for (LocalDate d = start; d.compareTo(end) <= 0; d = d.plusDays(1))
            if (d.getDayOfMonth() == 1 || d.getDayOfWeek() == DayOfWeek.MONDAY) ans++;
        System.out.println(ans);
    }
}

---

Java 6

---

  近两年写的代码了，

  那时蓝桥 $\mathrm{J}\mathrm{a}\mathrm{v}\mathrm{a}$ 的 $\mathrm{J}\mathrm{u}\mathrm{d}\mathrm{g}\mathrm{e}$ 还是 $\mathrm{J}\mathrm{D}\mathrm{K}1.6$。

  果然，

  还是没啥长进啊。

import java.text.DateFormat;
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Date;

public class Test {

	final static long oneDay = 1000 * 60 * 60 * 24;
	
    public static void main(String[] args) throws ParseException {
    	DateFormat format = new SimpleDateFormat("yyyy-MM-dd hh:mm:ss");
    	long start = format.parse("2000-01-01 00:00:00").getTime();
    	long end = format.parse("2020-10-01 00:00:00").getTime();
    	int cnt = 0;
    	while (start <= end) {
    		if (new Date(start).toString().contains("Mon") || new Date(start).toString().contains(" 01 ")) cnt += 2;
    		else cnt++;
    		start += oneDay;
    	}
    	System.out.println(cnt);
    }
}

---

不依赖 API 的实现

---

public class Test {

    public static void main(String[] args) { new Test().run(); }

    void run() {
        int year = 2000, month = 1, day = 1, week = 6, ans = 2;
        int[] days = { 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
        while (year != 2020 || month != 10 || day != 1) {
            if (day == 1 || week % 7 == 1) ans += 2;
            else ans++;
            if (++day > days[month] + (month == 2 && isLeapYear(year) ? 1 : 0)) {
                month++;
                day = 1;
            }
            if (month > 12) {
                month = 1;
                year++;
            }
            week++;
        }
        System.out.println(ans);
    }

    boolean isLeapYear(int year) { return year % 100 == 0 ? year % 400 == 0 : year % 4 == 0; }
}

  开胃题

---

#D 平面分割

本题总分：$10$ 分

---

问题描述

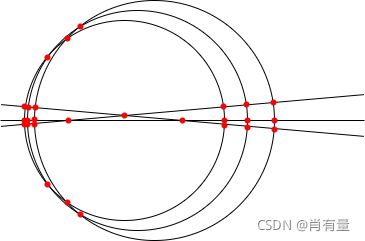
  $20$ 个圆和 $20$ 条直线最多能把平面分成多少个部分？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1319

---

平面几何

---

  $n$ 条直线能把平面最多分割的部分的个数是显然，

  我们使第 $i$ 条直线与前 $i-1$ 条直线相交，我们就又多了 $i$ 个平面。

  $n$ 个圆能把平面最多分割的部分的个数也是显然，

  就像绘制一个所有集合都有交集的交集图一样，我们使新加入的圆与之前的每个圆都相交有两点。

  这就足够启示我们，这类问题的结果的上界在哪，

  即即将加入的直线至多与已进行分割每条的直线有一个交点，与圆有两；

  即将加入的圆至多与已进行分割每个圆有两个交点，与直线同上；

  那么这种分割法真的可行吗？

  为了满足这种策略，我们将圆按圆心水平排列，用半径控制相交点的个数。

  然后往中间塞直线，保证每条直线都与圆交有两点。

  完事。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 20, M = 20;

    void run() {
        int ans = 1;
        for (int i = 1; i <= N; i++)
            ans += (i - 1) << 1;
        for (int i = 1; i <= M; i++)
            ans += (N << 1) + i;
        System.out.println(ans);
    }
}

  很讨厌这种题，

  但没办法，只能做。

---

#E 七段码

本题总分：$15$ 分

---

问题描述

  小蓝要用七段码数码管来表示一种特殊的文字。

  上图给出了七段码数码管的一个图示，数码管中一共有 $7$ 段可以发光的二极管，分别标记为 $a,b,c,d,e,f,g$。
  小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符的表达时，要求所有发光的二极管是连成一片的。
  例如：$b$ 发光，其他二极管不发光可以用来表达一种字符。
  例如：$c$ 发光，其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。
  例如：$a,b,c,d,e$ 发光，$f,g$ 不发光可以用来表达一种字符。
  例如：$b,f$ 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。
  请问，小蓝可以用七段码数码管表达多少种不同的字符？

---

答案提交

  这是一道结果填空题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

80

---

朴素解法

---

  建图、深搜、过。

  不过还是要注意一点，有环图上就别回溯了。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int a = 0, b = 1, c = 2, d = 3, e = 4, f = 5, g = 6;

    boolean[] selected = new boolean[7];

    boolean[] visited = new boolean[7];

    List<Integer>[] graph = new List[7];

    int ans = 0;

    void run() {
        for (int i = 0; i < 7; i++)
            graph[i] = new ArrayList();
        link(a, b);
        link(a, f);
        link(f, g);
        link(f, e);
        link(b, g);
        link(b, c);
        link(g, e);
        link(g, c);
        link(e, d);
        link(c, d);
        dfs(0, 0);
        System.out.println(ans);
    }

    void dfs(int depth, int length) {
        if (depth == 7) {
            if (length > 0) {
                int v = 0;
                while (!selected[v]) v++;
                Arrays.fill(visited, false);
                if (linkLength(v) == length) ans++;
            }
        } else {
            dfs(depth + 1, length);
            selected[depth] = true;
            dfs(depth + 1, length + 1);
            selected[depth] = false;
        }
    }

    int linkLength(int v) {
        visited[v] = true;
        int length = 1;
        for (int w : graph[v])
            if (selected[w] && !visited[w]) length += linkLength(w);
        return length;
    }

    void link(int v, int w) {
        graph[v].add(w);
        graph[w].add(v);
    }
}

---

分类讨论

---

  我们可以将七段码的显示方案简单归类为两种：

  包含 $g$ 的和不包含 $g$ 的，

  不包含 $g$ 的方案显然为 $5\times 6+1$，

  而包含 $g$ 的方案数我们可以讨论出半部取其的二次幂，

  也就是在选择 $g$ 时，$a,f,b$ 的合法方案数与 $c,d,e$ 相同，我们讨论出其中一种，将其结果与自己相乘就是包含 $g$ 的方案种数。

  而包含 $g$ 时，上半部方案数有 $2^3$，不合法的方案只有 $\{a\}$，

  故小蓝可以用七段码数码管表达 $5\times 6+1+(2^3-1{)}^2=80$ 种不同的字符。

---

#F 成绩分析

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$15$ 分

---

问题描述

  小蓝给学生们组织了一场考试，卷面总分为 $100$ 分，每个学生的得分都是一个 $0$ 到 $100$ 的整数。
  如果得分至少是 $60$ 分，则称为及格。如果得分至少为 $85$ 分，则称为优秀。
  请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整数。

---

输入格式

  输入的第一行包含一个整数 $n$，表示考试人数。
  接下来 $n$ 行，每行包含一个 $0$ 至 $100$ 的整数，表示一个学生的得分。

---

输出格式

  输出两行，每行一个百分数，分别表示及格率和优秀率。百分号前的部分四舍五入保留整数。

---

测试样例₁

Input：
7
80
92
56
74
88
100
0

Output：
71%
43%

---

评测用例规模与约定

  对于 $50$% 的评测用例，$1\le n\le 100$。
  对于所有评测用例，$1\le n\le 10000$。

---

  签到。

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt(), good = 0, best = 0;
        for (int i = 0, a; i < n; i++) {
            a = in.readInt();
            if (a >= 60) good++;
            if (a >= 85) best++;
        }
        System.out.printf("%.0f%%\n%.0f%%", 100f * good / n, 100f * best / n);
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

#G 单词分析

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$20$ 分

---

问题描述

  小蓝正在学习一门神奇的语言，这门语言中的单词都是由小写英文字母组成，有些单词很长，远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词，他准备不再完全记忆这些单词，而是根据单词中哪个字母出现得最多来分辨单词。
  现在，请你帮助小蓝，给了一个单词后，帮助他找到出现最多的字母和这个字母出现的次数。

---

输入格式

  输入一行包含一个单词，单词只由小写英文字母组成。

---

输出格式

  输出两行，第一行包含一个英文字母，表示单词中出现得最多的字母是哪个。如果有多个字母出现的次数相等，输出字典序最小的那个。
  第二行包含一个整数，表示出现得最多的那个字母在单词中出现的次数。

---

测试样例₁

Input：
lanqiao

Output：
a
2

测试样例₂

Input：
longlonglongistoolong

Output：
o
6

---

评测用例规模与约定

  对于所有的评测用例，输入的单词长度不超过 $1000$。

---

  双签到。

import java.io.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        try(BufferedReader in = new BufferedReader(new InputStreamReader(System.in))) {
            String word = in.readLine();
            int[] count = new int[0x100];
            for (int i = 0; i < word.length(); i++)
                count[word.charAt(i)]++;
            char ans = 'a';
            for (char i = 'a'; i <= 'z'; i++)
                if (count[i] > count[ans]) ans = i;
            System.out.println(ans);
            System.out.println(count[ans]);
        } catch (IOException e) {
            e.printStackTrace();
        }
    }
}

---

#H 数字三角形

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$20$ 分

---

问题描述

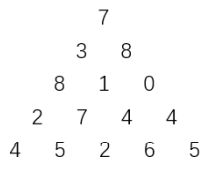
  上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。
  对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。
  路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 $1$。

---

输入格式

  输入的第一行包含一个整数 $N(1<N\le 100)$，表示三角形的行数。下面的 $N$ 行给出数字三角形。数字三角形上的数都是 $0$ 至 $100$ 之间的整数

---

输出格式

  输出一个整数，表示答案。

---

测试样例₁

Input：
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

Output：
27

---

  三签到了，

  本来以为是半个原创的线性$\mathrm{D}\mathrm{P}$，

  结果在向左下走的次数与向右下走的次数相差不能超过 $1$ 这个条件约束下，

  可达的终点就只剩下了底部对称轴边上的元素，

  不想出题可以 v 我几个米，我来出。

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt();
        int[][] dp = new int[2][n];
        for (int i = 1; i <= n; i++) {
            dp[i & 1][0] = in.readInt() + dp[i & 1 ^ 1][0];
            for (int j = 1; j < i; j++)
                dp[i & 1][j] = Math.max(dp[i & 1 ^ 1][j], dp[i & 1 ^ 1][j - 1]) + in.readInt();
        }
        System.out.println(Math.max(dp[n & 1][n >> 1], dp[n & 1][n - 1 >> 1]));
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

#I 作物杂交

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$25$ 分

---

问题描述

  作物杂交是作物栽培中重要的一步。已知有 $N$ 种作物 ( 编号 $1$ 至 $N$ )，第$i$ 种作物从播种到成熟的时间为 $T_i$。作物之间两两可以进行杂交，杂交时间取两种中时间较长的一方。
  如作物 $A$ 种植时间为 $5$ 天，作物 $B$ 种植时间为 $7$ 天，则 $AB$ 杂交花费的时间为 $7$ 天。作物杂交会产生固定的作物，新产生的作物仍然属于 $N$ 种作物中的一种。
  初始时，拥有其中 $M$ 种作物的种子 (数量无限，可以支持多次杂交)。同时可以进行多个杂交过程。求问对于给定的目标种子，最少需要多少天能够得到。
  如存在 $4$ 种作物 $ABCD$，各自的成熟时间为 $5$ 天、$7$ 天、$3$ 天、$8$ 天。初始拥有 $AB$ 两种作物的种子，目标种子为 $D$，已知杂交情况为 $A\times B\to C$，$A\times C\to D$。则最短的杂交过程为：

  1. 第 $1$ 天到第 $7$ 天 (作物 $B$ 的时间)，$A\times B\to C$。

  2. 第 $8$ 天到第 $12$ 天 (作物 $A$ 的时间)，$A\times C\to D$。

  花费 $12$ 天得到作物 $D$ 的种子。

---

输入格式

  输入的第 $1$ 行包含 $4$ 个整数 $N,M,K,T$，$N$ 表示作物种类总数 (编号 $1$ 至 $N$)，$M$ 表示初始拥有的作物种子类型数量，$K$ 表示可以杂交的方案数，$T$ 表示目标种子的编号。
  第 $2$ 行包含 $N$ 个整数，其中第 $i$ 个整数表示第 $i$ 种作物的种植时间 $T_i(1\le T_i\le 100)$。
  第 $3$ 行包含 $M$ 个整数，分别表示已拥有的种子类型 $K_j(1\le K_j\le M)$，$K_j$ 两两不同。
  第 $4$ 至 $K+3$ 行，每行包含 $3$ 个整数 $A,B,C$，表示第 $A$ 类作物和第 $B$ 类作物杂交可以获得第 $C$ 类作物的种子。

---

输出格式

  输出一个整数，表示得到目标种子的最短杂交时间。

---

测试样例₁

Input：
6 2 4 6
5 3 4 6 4 9
1 2
1 2 3
1 3 4
2 3 5
4 5 6


Output：
16

Explanation：
第 1 天至第 5 天，将编号 1 与编号 2 的作物杂交，得到编号 3 的作物种子。
第 6 天至第 10 天，将编号 1 与编号 3 的作物杂交，得到编号 4 的作物种子。
第 6 天至第 9 天，将编号 2 与编号 3 的作物杂交，得到编号 5 的作物种子。
第 11 天至第 16 天，将编号 4 与编号 5 的作物杂交，得到编号 6 的作物种子。
总共花费 16 天。

---

评测用例规模与约定

  对于所有评测用例，$1\le N\le 2000,2\le M\le N,1\le K\le 10^5,1\le T\le N$, 保证目标种子一定可以通过杂交得到。

---

图上动态规划

---

  显然在 $A\times B\to C$ 中，得到 $C$ 的时间为得到 $A$、$B$ 中最长时间加上培育 $A$、$B$ 的最长时间，

  但是每一种种子可能不止组成有一种方案，

  对应的，每个子问题可能会影响若干父问题，

  虽然解法和树上动态规划相同，但一个节点可能有若干父节点，因此它能算作图上问题。

  回到正题，有状态转移方程：$$dp(C)=\min \{\max (dp(A),dp(B))+\max (\mathrm{T}(\mathrm{A}),\mathrm{T}(\mathrm{B}))\}$$  懒得提细节了，

  本质还是签到题。

import java.util.*;
import java.io.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    List<Tuple>[] graph;

    int[] dp, T;

    void run() {
        InputReader in = new InputReader(System.in);
        int N, M, K, T, k, A, B, C;
        N = in.readInt();
        M = in.readInt();
        K = in.readInt();
        T = in.readInt();
        dp = new int[N + 1];
        graph = new List[N + 1];
        this.T = new int[N + 1];
        for (int i = 1; i <= N; i++) {
            graph[i] = new ArrayList();
            this.T[i] = in.readInt();
            dp[i] = -1;
        }
        for (int i = 0; i < M; i++) {
            k = in.readInt();
            dp[k] =0;
        }
        for (int i = 0; i < K; i++) {
            A = in.readInt();
            B = in.readInt();
            C = in.readInt();
            graph[C].add(new Tuple(A, B));
        }
        System.out.println(dp(T));
    }

    int dp(int T) {
        if (dp[T] != -1) return dp[T];
        int min = 0x3C3C3C3C;
        for (Tuple tuple : graph[T])
            min = Math.min(min, Math.max(dp(tuple.A), dp(tuple.B)) + Math.max(this.T[tuple.A], this.T[tuple.B]));
        return dp[T] = min;
    }

    class Tuple {

        int A, B;

        Tuple(int A, int B) {
            this.A = A;
            this.B = B;
        }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

#J 子串分值和

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$25$ 分

---

问题描述

  对于一个字符串 $S$，我们定义 $S$ 的分值 $f(S)$ 为 $S$ 中出现的不同的字符个数。例如 $f(“aba”)=2$，$f(“abc”)=3$, $f(“aaa”)=1$。
  现在给定一个字符串 $S[0..n-1]$（长度为 $n$），请你计算对于所有 $S$ 的非空子串 $S[i..j](0\le i\le j<n)$，$f(S[i..j])$ 的和是多少。

---

输入格式

  输入一行包含一个由小写字母组成的字符串 $S$。

---

输出格式

  输出一个整数表示答案。

---

测试样例₁

Input：
ababc

Output：
28

Explanation：
子串 f值
a     1
ab    2
aba   2
abab  2
ababc 3
b     1
ba    2
bab   2
babc  3
a     1
ab    2
abc   3
b     1
bc    2
c     1

---

评测用例规模与约定

  对于 $20$% 的评测用例，$1\le n\le 10$；
  对于 $40$% 的评测用例，$1\le n\le 100$；
  对于 $50$% 的评测用例，$1\le n\le 1000$；
  对于 $60$% 的评测用例，$1\le n\le 10000$；
  对于所有评测用例，$1\le n\le 100000$。

---

分类讨论

---

  给定字符串 $S$，若 $S$ 在 $i$ 处为字符 $c$，

  则我们可以将 $S$ 的子串简单分为两类：

  包含 $S[i]$，不包含 $S[i]$。

  显然对于两种情况，$c$ 对 $f(S^{\prime })$ 贡献是完全且没有重复的。

  不包含 $S[i]$ 的情况对应着在 $S[i+1,n]$ 上 $c$ 的贡献的问题，

  我们将 $c$ 出现的位置记做 $c_i$，特别地，我们将 $c_0$ 记作 $-1$，

  $c$ 在 $S$ 上能给出的贡献为$$f(S,c)=\sum _{i=1}^{count(S,c)}(c_i-c_{i-1})(n-c_i)$$  五道签到题，

  不想出可以不出真的。

import java.io.*;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        try (BufferedReader in = new BufferedReader(new InputStreamReader(System.in))) {
            String str = in.readLine();
            int[] last = new int[0x100];
            long n = str.length(), ans = 0;
            for (int i = 0; i < n; i++) {
                int c = str.charAt(i);
                ans += (i - last[c] + 1) * (n - i);
                last[c] = i + 1;
            }
            System.out.println(ans);
        } catch (IOException e) {
            e.printStackTrace();
        }
    }
}