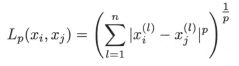【机器学习经典算法】K近邻(KNN)：核心与总结

1. 初识K近邻

K-近邻(K-Nearest Neighbors, KNN)可以说是整个机器学习算法中最为简单的几个算法之一了，但即使是在目前大火的深度学习算法里也可以看它的影子，简单好用，学起来就完事了。简单点来说，给定一个训练集，找到其映射到特征空间中的对应向量，保存下来。当新来了一个测试实例，找到其在特征空间中最近的K个实例，看在这K个实例中属于哪一个类别的最多，就给测试样本赋予对应的标签。

当K=1时，为最近邻算法

如上图所示，训练集有两类(蓝色、红色)，新来了一个样本(绿色)，要判断其属于哪一类。KNN算法就是在整个特征空间找到最近的K个参考对象(K=3)，这K个对象里属于哪一个类别的数目多，就是赋予新样本对应的标签。比如这个例子中新样本就为红色类别。

2. 相知

2.1 K近邻三要素

三个基本要素：K值选择、距离度量、分类决策规则

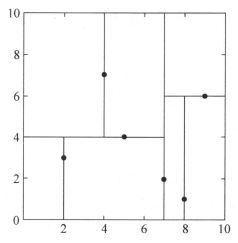
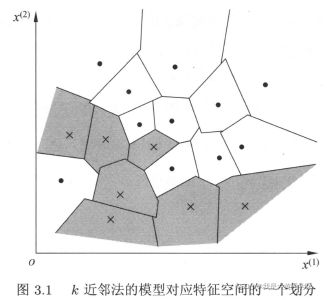
模型：模型很简单，上一节就已经介绍过了，更公式化的定义可以参考李航老师的《统计学习方法》。这里提一下模型的本质，抛去测试过程，当确定三要素后，KNN根据训练集样本将特征空间划分成不同子空间，每个子空间的类别被确定，如下图所示。(如果不理解这句话，可以考虑最近邻的情况)

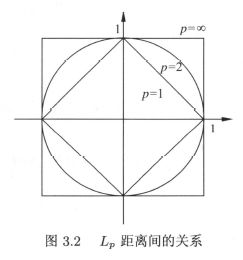
距离度量：常用的距离度量就是欧式距离，但其实任何距离度量都可以。这里展示一下$L_p$距离，不同的p有着不同的含义，这里就不展开讲了，贴一张图。

如下图所示，展示了$L_p$距离在p取不同时，在$R^2$空间上的一条等高线(线上的点与原点的距离相等)，感兴趣的同学可以扩展到损失函数中的L1、L2正则化。

需要注意的是，不同度量下得到的最近邻可能不一样

k值的选择：当K值较小时，那么在测试时选择的领域范围就大，学习的近似误差减小(只有与输入较近的实例才会对预测结果起作用)，估计误差增加(对近邻的实例点非常敏感，收益受噪声影响)；当K值过大时，选择的领域范围就大，会减小模型的估计误差，但会增加学习的近似误差。

也可以说k值越小，模型越复杂，越容易过拟合；K值越大，模型变简单，极端情况K=N时，所有输出都一样。

近似误差与估计误差：https://blog.csdn.net/qq_35664774/article/details/79448076

k值一般取一个比较小的数值，通常采用交叉验证法来选取最优的k值。

分类决策规则：多数表决（等价于经验风险最小化，证明见《统计学习方法》）

2.2 KD树

k 近邻法最简单的实现方法是线性扫描(linear scan)，即计算输入实例与每一个训练实例的距离。但当训练集很大时，这种方法非常耗时。而KD树(k-dimensional tree)可以提高搜索效率，减少计算量。kd树是一种对k维空间中的实例点进行储存以便对其进行快速检索的树形数据结构，其本质是二叉树，可以将最近邻的搜索时间由$O(N)$降低到$O(NlogN)$。

2.2.1 kd树的构建

kd树构建的核心思想就是递归地对数据进行垂直划分，具体流程如下：

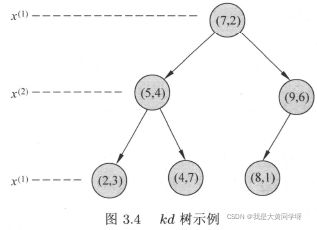
其中(1)表示递归的初始条件，(2)表示递归逻辑，(3)为终止条件。上面的算法流程可能比较难以理解，其实通俗点理解就是：对于N个k维的训练数据，knn需要将其划分为N个区域，首先选取第一个维度，将所有数据按整个维度进行排序，选取中位数所对应的节点作为根节点。在该维度上小于该节点的值划分到左子树，大于该节点的值划分到右子树。这样就已经先划分成两个区域了，然后选取第二个维度，分别对这2个区域进行类似的划分（找到中位数节点进行划分），就这样依次递归下去，知道所有子区域都没有实例存在。【整个过程类似于平衡二叉搜索树的构建】

强烈推荐该视频：https://www.bilibili.com/video/BV1No4y1o7ac?p=21，看完你就懂了，也包含了实例的讲解。

2.2.2 kd树的搜索

kd树主要是为了加速KNN的检索过程，也就是说给定一个测试样本，去找到它对应的K个最近邻样本。以最近邻为例(很容易扩展到k近邻)，其仍是一个递归的过程。具体流程如下：

对于构造的kd树，首先按照每个维度对应的划分找到一个叶子节点，将该叶子节点作为ans。递归地进行回退：首先检查该节点的兄弟节点是否比这个叶子节点更近，如果更近则进行转移，否则回退到父节点，然后计算距离是否更近，如果更近就更新ans。最后回退到根节点，就搜索结束，返回的ans即为最近邻节点。

对应的视频与示例：https://www.bilibili.com/video/BV1No4y1o7ac?p=22

3. 总结

KNN是最简单的分类与回归算法，虽然上面只介绍了分类的步骤，但是回归方法也是类似，进行KNN然后求均值作为结果返回。KNN三大要素：距离度量、k值选择、分类决策规则，其中K值越小模型越复杂，近似误差低，K值越大模型越简单，估计误差低。

K近邻算法虽然简单，但其局限性也非常明显。算法并没有根据数据显著地构建一个模型，而是存储了所有训练集特征，当训练数据很大时，时间和空间复杂度将会非常高。因此为了进一步提高计算效率，采用kd树进行优化。