<数据结构>链式二叉树的基本操作
文章目录
- 1. 前置说明
- 2. 二叉树的遍历
-
- 2.1 二叉树前序遍历
- 2.2 二叉树中序遍历
- 2.3 二叉树后序遍历
- 2.4 二叉树层序遍历
- 3. 二叉树节点个数 (引进分治思想)
- 4. 二叉树叶子节点个数
- 5. 二叉树第k层节点个数
- 6. 二叉树层数
- 7. 二叉树查找值为x的节点
- 8. 判断是否为完全二叉树
- 9. 二叉树的销毁
目前在不断更新<数据结构>的知识总结,已经更新完了
,未来我会系统地更新 等内容。
| 想要一步步稳扎稳打,学习编程的小伙伴可以关注我或者订阅专栏,文章都是免费的,不要错过这一个提升自己的机会! |
普通二叉树的增删查改没有价值,如果是为了单纯存储数据,不如使用线性表
我们这一节的学习是为了更好的控制它的结构,为之后学习更复杂的搜索二叉树打基础。并且很多二叉树的OJ算法题都出在普通二叉树上。
1. 前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二
叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树
操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
BTNode* BuyBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
assert(node);
node->data = x;
node->left = node->right = NULL;
return node;
}
BTNode* CreateBinaryTree()
{
BTNode* node1 = BuyBTNode(1);
BTNode* node2 = BuyBTNode(2);
BTNode* node3 = BuyBTNode(3);
BTNode* node4 = BuyBTNode(4);
BTNode* node5 = BuyBTNode(5);
BTNode* node6 = BuyBTNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,
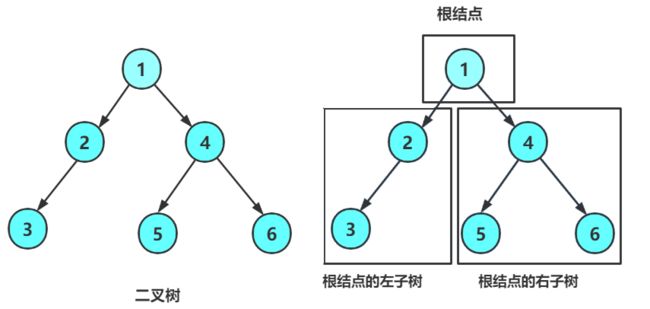
二叉树是:
空树
非空:根节点,根节点的左子树、根节点的右子树组成的
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的
2. 二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
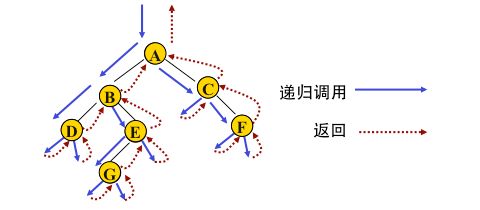
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1️⃣前序遍历——访问根结点的操作发生在遍历其左右子树之前。(根➡️左子树➡️右子树)
2️⃣中序遍历——访问根结点的操作发生在遍历其左右子树之中(间)。(左子树➡️根➡️右子树)
3️⃣后序遍历——访问根结点的操作发生在遍历其左右子树之后。 (左子树➡️右子树➡️根)
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
除了深度优先遍历(DFS):先序遍历、中序遍历、后序遍历外,还可以对二叉树进行广度优先遍历(BFS):层序遍历。
层序遍历——自上而下,自左至右逐层访问
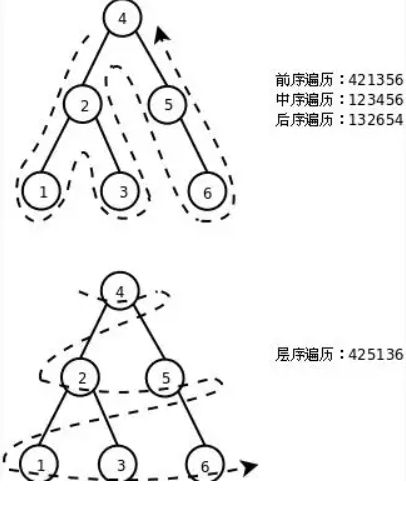
2.1 二叉树前序遍历
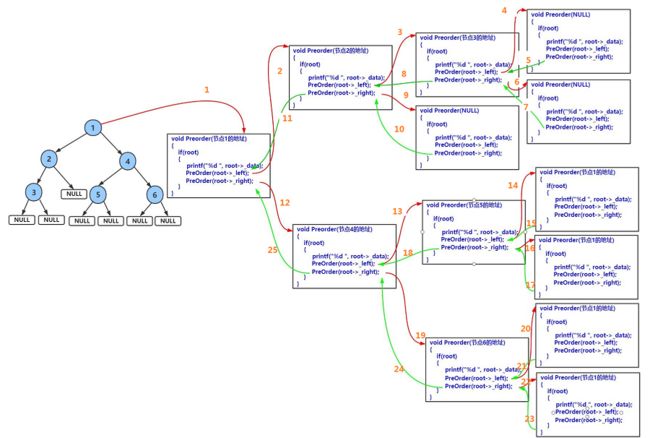
按橙色序号顺序看,效果更好!
顺序:根➡️左子树➡️右子树
解析:(相同颜色代表遍历同一个根的左子树和右子树,搭配上面的图解和下面的动图一同食用效果更佳<( ̄︶ ̄)>)
根(1)
根(1)的左子树(2)
此时2成了新的根,根(2)的左子树(3)
此时3成了新的根,根(3)的左子树(NULL)
回退,访问根(3)的右子树(NULL)
回退,访问根(2)的右子树(NULL)
回退,访问根(1)的右子树(4)
此时4成了新的根,根(4)的左子树(5)
此时5成了新的根,根(5)的左子树(NULL)
回退,访问根(5)的右子树(NULL)
回退,访问根(4)的右子树(6)
此时6成了新的根,根(6)的左子树(NULL)
回退,访问根(6)的右子树(NULL)
回退到6,再回退到4,最后整棵树都遍历完毕了
前序遍历结果:1 2 3 4 5 6
如果还不理解建议看看递归的知识复习一下,c语言自学教程——函数是我好久之前写的,最后一部分详细地讲了递归
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);//根
PreOrder(root->left);//左子树
PreOrder(root->right);//右子树
}
2.2 二叉树中序遍历
你已经是个大人了,要学会自己分析、理解啦。
中序和后序遍历跟前序遍历的思路一模二样,在这就不详细画图解释咯。 (*•̀ㅂ•́)و
顺序:左子树➡️根➡️右子树
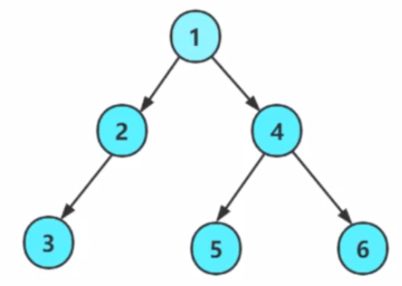

中序遍历结果:3 2 1 5 4 6
void InOrder(BTNode* root)//中序
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
2.3 二叉树后序遍历
顺序:左子树➡️右子树➡️根


后序遍历结果:3 2 5 6 4 1
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
InOrder(root->right);
printf("%d ", root->data);
}
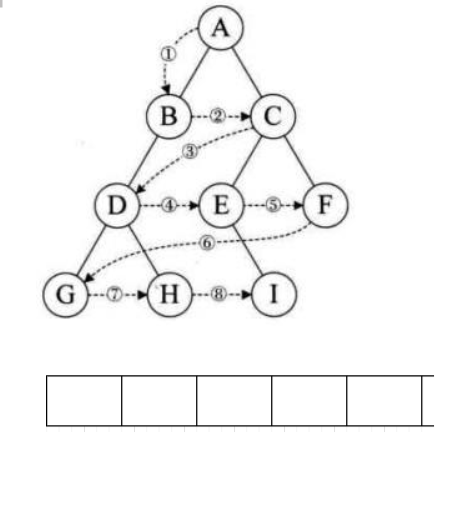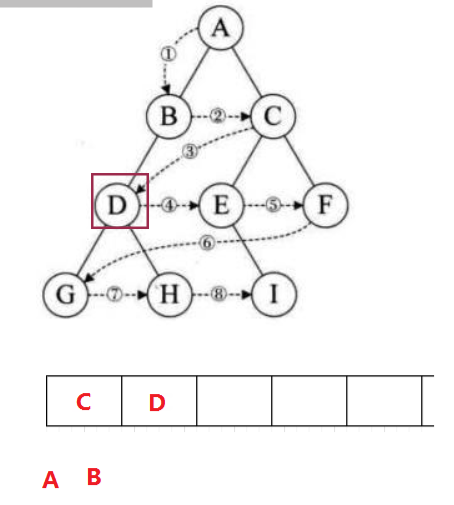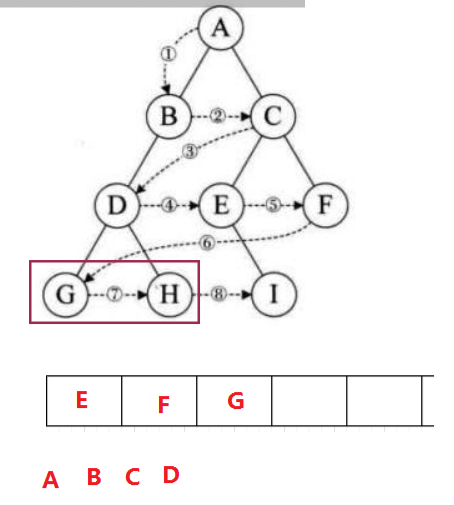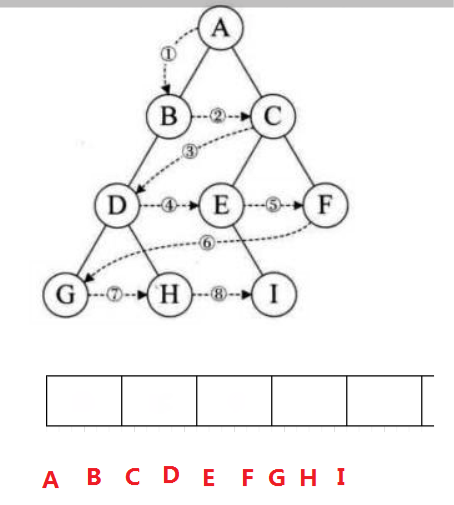
2.4 二叉树层序遍历
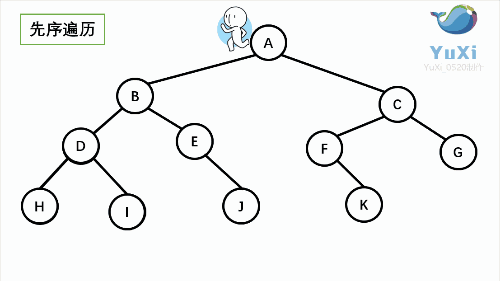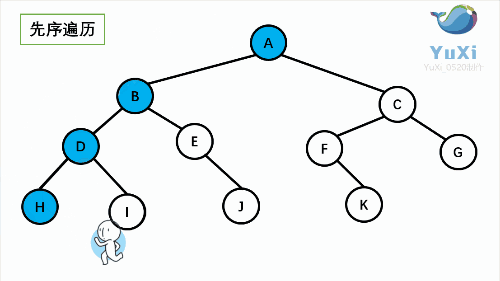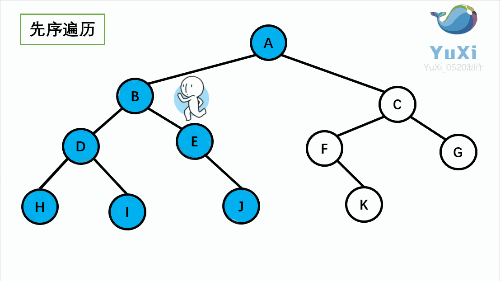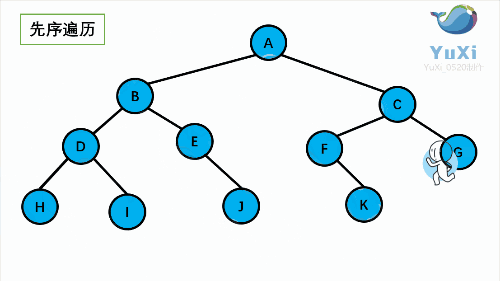
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
思路:先把根入队列,运用队列先进先出的性质,上一层的节点出的时候,带下一层的节点进去(在节点不为空的情况下‼️)。
层序遍历结果:A B C D E F G H I
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
QueueDestory(&q);
}
3. 二叉树节点个数 (引进分治思想)
方法一:(遍历+计数)
遍历中会新建栈帧,每个栈帧都定义一个count没法加到一起,所以定义一个全局变量、或静态变量
int count = 0;//全局变量
//思想:遍历+计数
int BTreeSize(BTNode* root)
{
if (root == NULL)
return;
count++;
BTreeSize(root->left);
BTreeSize(root->right);
return count;
}
int main()
{
count = 0;
printf("size:%d\n", BTreeSize(tree));
count = 0;
printf("size:%d\n", BTreeSize(tree));
}
缺点:多次调用count会累加,每次调用还得初始化一次count(还会有线程安全的问题,这个以后linux学了大家就知道了)
改进版:传变量地址
//思想:遍历+计数
void BTreeSize(BTNode* root, int* pCount)
{
if (root == NULL)
return;
(*pCount)++;
BTreeSize(root->left, pCount);
BTreeSize(root->right, pCount);
}
int main()
{
int count1 = 0;
BTreeSize(tree, &count1);
printf("size:%d\n", count1);
}
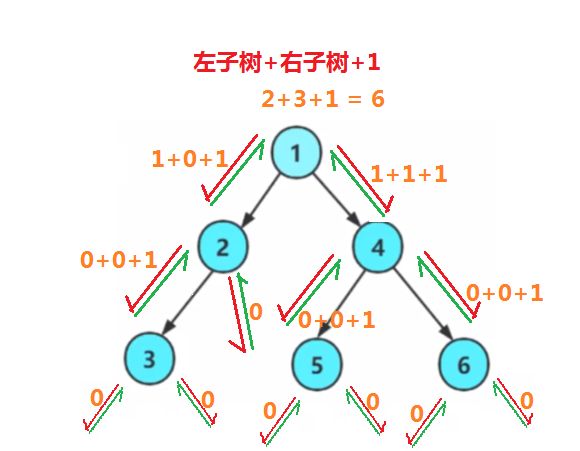
方法二:(分治:把复杂问题分成更小规模子问题···直到子问题不可再分割,能直接能出结果)
思路:分治(超级套娃)
1️⃣空数,最小规模的子问题,节点个数返回0
2️⃣非空,左子树节点个数+右子树节点个数+1(自己)
图解:
//思想:分治
int BTreeSize(BTNode* root)
{
return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
4. 二叉树叶子节点个数
思路:叶子节点个数 = 左子树的叶子节点 + 右子树的叶子节点
int BTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
//判断是否为叶子节点
if (root->left == NULL && root->right == NULL)
return 1;
return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}
5. 二叉树第k层节点个数
不想画图了╮(๑•́ ₃•̀๑)╭,自己尝试画画吧
假如我要求第三层的节点个数,怎么才能知道那是第三层呢?
我可以在第一层求它下下层的节点个数
我可以在第二层求它下一层的节点个数
就可以转换成求第一层向下k-1层的节点个数
思想:
1️⃣空数,返回0
2️⃣非空,且k == 1,返回1
3️⃣非空,且k > 1,转换成左子树k-1层节点个数 + 右子树k-1层节点个数
//第k层节点个数
int BTreeLevelSize(BTNode* root, int k)
{
assert(k >= 1);
if (root == NULL)
return 0;
if (k == 1)
return 1;
return BTreeLevelSize(root->left, k - 1) + BTreeLevelSize(root->right, k - 1);
}
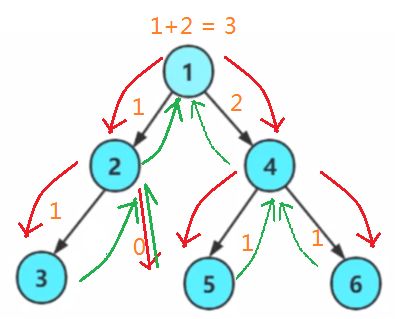
6. 二叉树层数
思路:层数 =
左子树高度和右子树高度中大的那个+1
int BTreeDepth(BTNode* root)
{
if (root == NULL)
return 0;
int leftDepth = BTreeDepth(root->left);
int rightDepth = BTreeDepth(root->right);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
7. 二叉树查找值为x的节点
思路:从根开始找,按照前序遍历顺序找,找到就返回地址,找不到就返回NULL
BTNode* BTFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* ret1 = BTFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = BTFind(root->right, x);
if (ret2)
return ret2;
return NULL;
}
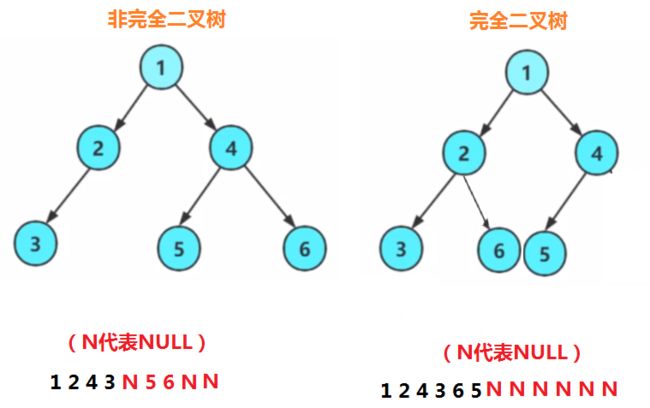
8. 判断是否为完全二叉树
还记得上面写的层序遍历吗?
我们要运用它巧妙地解决这道题。
思路:
层序遍历,空节点也入队列、出队列
当出到第一个NULL时停止入队列,只出队列
判断NULL后是否全为NULL,还是说其中有节点的值乱入(下图红色部分)
//是否为完全二叉树
//层序遍历,空节点也出,判断空之后是否都为空
bool BTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//出到空,就判断后续
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//出到非空——不是完全二叉树
if (front)
return false;
}
QueueDestory(&q);
return true;
}
9. 二叉树的销毁
玩完之后要记得销毁哦!
想一想,能不能从根节点开始销毁呢?
不能,否则就找不到下面的节点了
所以,我们要用后续遍历的顺序来销毁,最后销毁根节点
void BTDestory(BTNode* root)
{
if (root == NULL)
return;
BTDestory(root->left);
BTDestory(root->right);
free(root);
}
小结:
这节的内容难度又上了一个台阶,考察的不仅是对数据结构的理解,还有c语言阶段对递归的理解。
加油哦,就算走得慢也比原地踏步好。