统计学习笔记-第7章 支持向量机
第七章 支持向量机(Support Vector Machines, SVM)
前言
支持向量机这部分的知识点断断续续看了一周,看的头疼,至今仍有许多疑惑。在理解透彻之前先记下部分总结,也包括一些不懂的点,整理一下看的知识点,等有时间再回过头来仔细看看。
支持向量机(Support Vector Machine, SVM)的大名想必大家早有耳闻,其功能强大且用途广泛,既可以进行线性分类也可以进行非线性分类,甚至还可以进行异常值检测。SVM最大的优点是适用于小或中等样本量的复杂数据集。
作为定义在特征空间上的线性分类器,SVM有别于感知机的一点是它采用了间隔最大化的一个学习策略,可以形式化为一个求解凸二次规划(convec quadratic programming)的问题。
SVM从简单到复杂分为:
- 线性可分支持向量机(linear support vector machine in linearly separable case)
- 线性支持向量机(linear support vector machine)
- 非线性支持向量机(non-linear support vector machine)。
简单的模型是复杂模型的基础,而复杂模型是简单模型的特殊情况,类似于马哲中个性与共性的关系。三种模型的区分如下:
- 训练数据可分,通过硬间隔最大化(hard margin maximization),得到一个线性分类器,即线性可分支持向量机,也称硬间隔支持向量机
- 训练数据接近线性可分时,通过软间隔最大化(soft margin maximization),得到的线性分类器,即线性支持向量机,又称为软间隔支持向量机
- 训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机
以下按照上述所述的顺序介绍三种SVM、核函数以及SVM快速学习方法——序列最小最优化算法(SMO)
7.1 线性可分支持向量机与硬间隔最大化
7.1.1 线性可分支持向量机
首先给出线性可分支持向量机的训练数据描述,假设给定一个特征空间上的训练数据集
T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) T={(x_1,y_1), (x_2, y_2),…,(x_N,y_N)} T=(x1,y1),(x2,y2),…,(xN,yN)
其中, x i ∈ X = R n x_i\in X = R^n xi∈X=Rn,即 x i = ( x 11 , x 12 , … , x 1 m ) T x_i = (x_{11}, x_{12}, …, x_{1m})^T xi=(x11,x12,…,x1m)T, y i ∈ Y = { + 1 , − 1 } , i = ( 1 , 2 , … , N ) y_i \in Y = \{+1, -1\},i=(1,2,…,N) yi∈Y={+1,−1},i=(1,2,…,N), x i x_i xi 为第 i i i 个特征向量,被称为实例,每个实例的维数为 m m m,即特征维度为 m m m 维, y i y_i yi 是 x i x_i xi 的标记,当 y i = + 1 y_i = +1 yi=+1 时,称 x i x_i xi 为正例;当 y i = − 1 y_i=-1 yi=−1 时,称 x i x_i xi 为负例,假设此时训练数据集是线性可分的。
分类学习最基本的思想是在样本空间找到一个划分超平面,将不同的类别的样本划分开来。线性可分支持向量机利用间隔最大化求最优分离超平面,这时,解是唯一的。
如下图所示,左图为普通的分割,其中除了绿色点线,都正确地分类,但是分割平面离实例点很近,如果训练数据有特异值或者误差,就不能很好地预测。右图是采用间隔最大化策略分割的SVM分类器分割的结果,可以看到这条分割线不仅将两类分隔开来而且离最近的训练实例尽可能的远。

这样我们给出了线性可分支持向量机的一个定义
定义 7.1 (线性可分支持向量机) 给定线性可分训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为
w ∗ x + b ∗ = 0 w^*x+b^*=0 w∗x+b∗=0
以及相应的分类决策函数
f ( x ) = s i g n ( w ∗ x + b ∗ ) f(x)=sign(w^*x+b^*) f(x)=sign(w∗x+b∗)
称为线性可分支持向量机
其中超平面的参数 w = ( w 1 , w 2 , w 3 , … , w m ) w=(w_1, w_2, w_3, …, w_m) w=(w1,w2,w3,…,wm) ,即 w w w 属于 m m m 列的一维矩阵, b b b是一个系数, s i g n sign sign 是判断函数,大于0为正,否则为负。
其中线性可分意味着有许多直线可以将两类数据正确分类,而其中SVM对应着其中间隔最大的一条直线。
数据线性可分是指对于数据集 { ( x i , y i ) } ( i = 1 N ) \{(x_i,y_i)\}(i=1~N) {(xi,yi)}(i=1 N), ∃ ( w , b ) \exists (w,b) ∃(w,b) 对于 ∀ i = 1 N \forall i=1~N ∀i=1 N 有若 y i = + 1 y_i=+1 yi=+1,则 w T x i + b ≥ 0 w^T x_i + b \geq 0 wTxi+b≥0;若 y = − 1 y=-1 y=−1,则 w T x i + b < 0 w^T x_i + b < 0 wTxi+b<0
那么如何计算 w w w 和 b b b 值呢?在回答这个问题之前,我们需要注意,SVM的学习策略是间隔最大化,以下介绍函数间隔和几何间隔,通过间隔问题得到最优化问题。
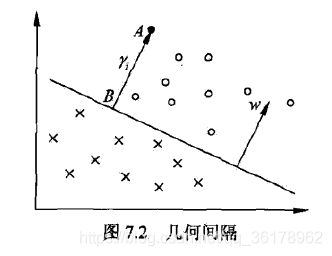
7.1.2 函数间隔和几何间隔
直接给出函数间隔(functional margin)的定义如下
定义 7.2 (函数间隔) 对于给定的训练数据集 T T T 和超平面 ( w , b ) (w,b) (w,b),定义超平面 ( w , b ) (w,b) (w,b) 关于样本点 $(x_i, y_i) 的函数间隔为
r i ^ = y i ( w ⋅ x i + b ) (7.3) \hat{r_i}=y_i(w \cdot x_i +b) \tag{7.3} ri^=yi(w⋅xi+b)(7.3)
定义超平面 ( w , b ) (w,b) (w,b) 关于训练数据集 T T T 的函数间隔为超平面 ( w , b ) (w,b) (w,b) 关于 T T T 中所有样本点 ( x i , y i ) (x_i, y_i) (xi,yi) 的函数间隔之最小值,即
r ^ = min i = 1 , … , N r i ^ (7.4) \hat{r}=\min \limits_{i=1,…,N} \hat{r_i} \tag{7.4} r^=i=1,…,Nminri^(7.4)
其中 w ⋅ x i w \cdot x_i w⋅xi 表示两个矩阵的内积,函数间隔可以表示分类预测的正确性及确信度。
但是值得注意一点是,如果成比例的改变 w w w 和 b b b ,超平面没有发生变化,但是函数间隔却发生变化。因此,我们对分离超平面的法向量 w w w 加某些约束,如规范化, ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1,这样间隔是确定的。这时得到的函数间隔也被称作几何间隔(grometric margin),几何间隔的定义如下所示
定义 7.2 (几何间隔) 对于给定的训练数据集 T T T 和超平面 ( w , b ) (w,b) (w,b),定义超平面 ( w , b ) (w,b) (w,b) 关于样本点 $(x_i, y_i) 的几何间隔为
r i ^ = y i ( w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ ) (7.5) \hat{r_i}=y_i(\frac{w}{||w||} \cdot x_i +\frac{b}{||w||}) \tag{7.5} ri^=yi(∣∣w∣∣w⋅xi+∣∣w∣∣b)(7.5)
定义超平面 ( w , b ) (w,b) (w,b) 关于训练数据集 T T T 的几何间隔为超平面 ( w , b ) (w,b) (w,b) 关于 T T T 中所有样本点 ( x i , y i ) (x_i, y_i) (xi,yi) 的几何间隔之最小值,即
r ^ = min i = 1 , … , N r i ^ (7.6) \hat{r}=\min \limits_{i=1,…,N} \hat{r_i} \tag{7.6} r^=i=1,…,Nminri^(7.6)
其中 ∣ ∣ w ∣ ∣ = w 1 2 + w 2 2 + … + w m 2 ||w|| = \sqrt{w_1^2+w_2^2+…+w_m^2} ∣∣w∣∣=w12+w22+…+wm2 为 w w w 的 L 2 L_2 L2 范数
超平面 ( w , b (w,b (w,b 关于样本点 ( x i , y i ) (x_i, y_i) (xi,yi) 的几何间隔一般是实例点到超平面的带符号距离(signed distance),当样本点被超平面正确分类时就是实例点到超平面的距离
由定义 ( 7.3 ) − ( 7.6 ) (7.3)-(7.6) (7.3)−(7.6) 得到函数间隔与几何间隔的关系如下所示:
r i = r i ^ ∣ ∣ w ∣ ∣ (7.7) r_i = \frac{\hat{r_i}}{||w||} \tag{7.7} ri=∣∣w∣∣ri^(7.7)
同理有:
r = r ^ ∣ ∣ w ∣ ∣ (7.8) r=\frac{\hat{r}}{||w||} \tag{7.8} r=∣∣w∣∣r^(7.8)
几何间隔与函数间隔的区别如下所示:
- 若 ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1,那么函数间隔与几何间隔相等
- 如果 w , b w, b w,b 按比例改变(超平面没有改变),函数间隔按比例改变,但是几何间隔不会变化
后续会利用到第二个特点化简等式
7.1.3 间隔最大化
在数据线性可分的假设条件下,可以正确分类的超平面有无数多个,如何找出最优秀的超平面?这里引入一个判定优秀超平面的方法,间隔最大化(margin maximization)。
间隔最大化的直观解释是:
对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类
也就是说,不仅要分类正确,还要分的足够开. 这样的超平面应该对未知的新实例有很好的分类预测能力.
1. 最大间隔分离超平面
以下是推导如何获取一个几何间隔最大的分离超平面, 这部分的数学公式比较复杂, 本来打算直接截图的, 但是这样既不美观, 也偏离了复习SVM的初衷. 这里以我自己的理解对这部分进行简要的复述.
将求解最大间隔分离超平面的问题表示为一个约束最优化问题:
max w , b r (7.9) \max_{w, b} \quad r \tag{7.9} w,bmaxr(7.9)
s . t . y i ( w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ ) ≥ r , i = 1 , 2 , . . . , N (7.10) s.t. \quad y_i \bigg(\frac{w}{||w||} \cdot x_i + \frac{b}{||w||}\bigg)\geq r,\quad i=1,2,...,N \tag{7.10} s.t.yi(∣∣w∣∣w⋅xi+∣∣w∣∣b)≥r,i=1,2,...,N(7.10)
在约束条件为超平面 ( w , b ) (w, b) (w,b) 关于每个训练样本点的几何间隔至少是 r r r 的前提下,最大化超平面 ( w , b ) (w,b) (w,b) 关于训练数据集的几何间隔 r r r.
根据式 ( 7.8 ) (7.8) (7.8) ,将几何间隔代替为函数间隔:这个问题改写为:
max w , b r ^ ∣ ∣ w ∣ ∣ (7.11) \max_{w, b} \quad \frac{\hat{r}}{||w||} \tag{7.11} w,bmax∣∣w∣∣r^(7.11)
s . t . y i ( w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ ) ≥ r ^ ∣ ∣ w ∣ ∣ , i = 1 , 2 , . . . , N (7.12) s.t. \quad y_i \bigg(\frac{w}{||w||} \cdot x_i + \frac{b}{||w||}\bigg) \geq \frac{\hat{r}}{||w||},\quad i=1,2,...,N \tag{7.12} s.t.yi(∣∣w∣∣w⋅xi+∣∣w∣∣b)≥∣∣w∣∣r^,i=1,2,...,N(7.12)
函数间隔 r ^ \hat{r} r^ 的取值不会影响最优化问题的解. 且将 w , b w, b w,b 等比例的改变为 λ w , λ b \lambda w, \lambda b λw,λb, 这时函数间隔为 λ r ^ \lambda \hat{r} λr^. 函数间隔的改变对上述最优化问题的不等式约束没有影响, 对目标函数的优化也没有影响. 所以简化上述公式, 取 r ^ = 1 \hat{r}=1 r^=1, 且注意到最大化 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 和最大化 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}||w||^2 21∣∣w∣∣2 是等价的,所以得到以下线性可分支持向量机学习的最优化问题
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 (7.13) \min_{w, b} \quad \frac{1}{2} ||w||^2 \tag{7.13} w,bmin21∣∣w∣∣2(7.13)
s . t . y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , 2 , . . . , N (7.14) s.t. \quad y_i (w \cdot x_i + b) -1 \geq 0,\quad i=1,2,...,N \tag{7.14} s.t.yi(w⋅xi+b)−1≥0,i=1,2,...,N(7.14)
- 这里 max w , b 1 ∣ ∣ w ∣ ∣ \max_{w, b}\frac{1}{||w||} maxw,b∣∣w∣∣1 与 min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min_{w, b}\frac{1}{2} ||w||^2 minw,b21∣∣w∣∣2 等价推导过程如下:
最大化 1 ∣ ∣ w ∣ ∣ ⇒ \frac{1}{||w||} \Rightarrow ∣∣w∣∣1⇒ 最大化 ∣ ∣ w ∣ ∣ ⇒ ||w|| \Rightarrow ∣∣w∣∣⇒ 为后续求导方便, 将 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 改写为 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}||w||^2 21∣∣w∣∣2- 限制条件从式 ( 7.12 ) (7.12) (7.12) 到式 ( 7.14 ) (7.14) (7.14) 是取 r ^ = 1 \hat{r} = 1 r^=1 并不等式左右同时乘上 ∣ ∣ w ∣ ∣ ≥ 0 ||w|| \geq 0 ∣∣w∣∣≥0
这是一个凸二次规划(convex quadratic programming)问题
凸优化问题是指约束最优化问题
min w f ( w ) (7.15) \min_w \quad f(w) \tag{7.15} wminf(w)(7.15)
s . t . g i ( w ) ≤ 0 , i = 1 , 2 , . . . , k (7.16) s.t. \quad g_i(w) \leq 0, \quad i=1,2,...,k \tag{7.16} s.t.gi(w)≤0,i=1,2,...,k(7.16)
h i ( w ) = 0 , i = 1 , 2 , . . . , l (7.17) h_i(w)=0, \quad i=1,2,...,l \tag{7.17} hi(w)=0,i=1,2,...,l(7.17)
其中, 目标函数 f ( w ) f(w) f(w) 是二次函数且约束函数 g i ( w ) g_i(w) gi(w) 都是 R n R^n Rn 上的连续可微的凸函数, 约束函数 h i ( w ) h_i(w) hi(w) 是 R n R^n Rn 上的仿射函数.
当目标函数 f ( w ) f(w) f(w) 是二次函数且约束函数 g i ( w ) g_i(w) gi(w) 是仿射函数(一次函数)时,上述凸优化问题成为凸二次规划问题. 其要么无解, 要么有解且唯一.
凸二次规划问题的局部极值也是全局极值
凸函数的一般图像如下图所示
结合式 ( 7.13 ) − ( 7.14 ) (7.13)-(7.14) (7.13)−(7.14) 得到最大间隔法(maximum margin method)
2. 最大间隔分离超平面的存在唯一性
线性可分训练数据集的最大间隔分离超平面是存在且唯一的
这里给出了最大间隔法求解唯一的理论支持
定理 7.1 (最大间隔分离超平面的存在唯一性) 若训练数据集 T T T 线性可分,则可将训练数据集中的样本点完全正确分开的最大间隔分离超平面存在且唯一.
具体的证明可以参考[1]中p117-p118
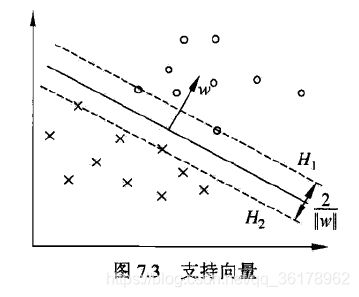
3. 支持向量和间隔边界
参考文献
[1]. 李航. 统计学习方法(第二版) [M ].北京: 清华大学出版社.2019
[2]. 周志华. 机器学习[M].北京: 清华出版社. 2016
[3]. Aurélien Géron.Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow[M]. America:O’Reilly Media, Inc.2019, June.