《机器学习算法的数学解析与python实现》学习笔记（第一章）
前言：
本人是研一新生，刚开始接触机器学习，这本书是今天刚去图书馆借的，今天一口气读了四章，作者的描写非常细致，写的非常不错，不会一开始接触，觉得晦涩难懂，对算法的数学解析也描写的很不错，详细介绍了多个非常经典的机器学习算法，强推零基础的学生和爱好者去翻看。第一次写学习笔记，内容有表述不清楚的，欢迎留言指正。
一、机器学习概述
1. 1 什么是机器学习
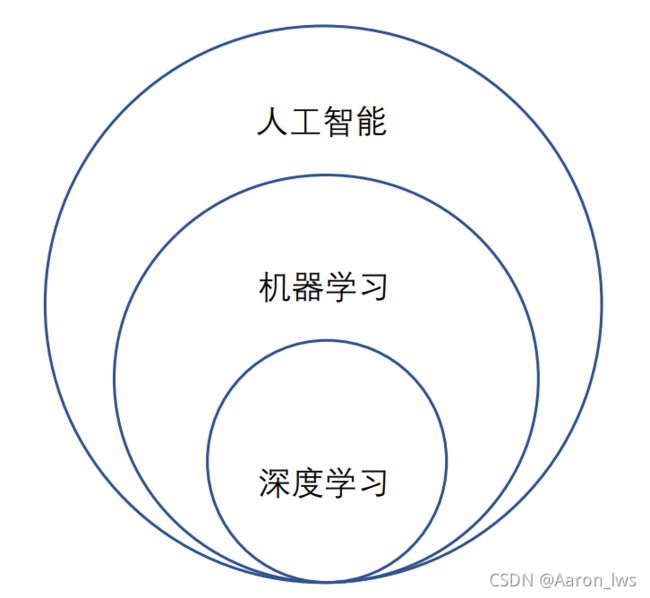
首先，我们要先了解，机器学习与人工智能和深度学习的关系，如下图：
图 1-1 人工智能、机器学习和深度学习三者的包含关系
人工智能：涵盖范围非常广泛，关注的问题和方法杂且多，包括机器人，逻辑规划等。
机器学习：该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能。当前发展非常迅猛，子算法流派枝繁叶茂。
深度学习：原本是在机器学习的神经网络子算法分支中发展出来的一系列成果，随着近年来的火热，人们渐渐将这一概念独立出来，单独起了个名字“单飞”了，由此有了深度学习和传统机器学习的区分。
注：因为深度学习近年的火爆，在科研或企业上备受青睐，很多同学忍不住想尽快上手深度学习，但个人建议是先学好机器学习，再慢慢过渡，打好基础。
1. 2 机器学习的几个需求层级
”一口吃不成个胖子“。机器学习确实是一门算法科学，数学是它背后的源泉和依靠。但如果一头扎入：概率论，微积分，线性代数还有编程技术里，会毫无目的性。机器学习的诞生是为了去解决实际问题。所以，明确自己的目的，要解决什么问题，才能决定自己需要学什么知识，学到什么程度。
设计需求层次：只需要考虑两件事：一、我们要做什么，二、程序能做什么。至于程序怎么去实现，那是后面的事。
调用需求层次：身为调用者，将机器学习算法和算法库进行调用，使其能解决实际问题。
数学需求层次：作为有一些经验的开发者，学习目标是拓展某个领域如算法，问题和工具等。
1. 3 机器学习的基本原理
机器学习，作者用另外一个词形容：统计模型训练。机器学习一项主要工作是”训练模型“。
机器学习的过程，就是一个“猜”的过程，一直不断重复两个问题：“我猜的是什么”和“我猜中了没有”。根据“我猜的是什么”的结果回答“我猜中没有”，再根据“我猜中没有”的结果来回答“我猜的是什么”。
机器学习的训练过程中，算法模型（机器学习术语，后续会详细介绍）会根据用户“喂”给它的数据集，来输出一个数值，损失函数（机器学习术语，后续会详细介绍）经过计算，回馈一个偏差结果，算法模型再根据这个结果来进行调整，再输出数值，这样周而复始，直到正确，这就是机器学习训练过程，这过程称为”拟合“。
1. 4 机器学习的基本概念
数据集：数据集可分为训练集和测试集，两个的内容和形式无差异，只是用在不同地方：训练集是在前期训练模型时候使用，”喂“给机器学习模型去进行训练的”燃料“；测试集是为了检测训练好的模型是否达标。
模型：机器学习的两大组成部分是模型 + 数据集。模型是机器学习算法在通过大量数据学习后，不断去调整参数后的产物。
数据：数据的集合就是数据集。在机器学习中，一条数据称为一个样本(Sample)，形式类似一维数组。样本通常包含多个特征。
特征：在数据这个类似一维数组的形式上，特征就是其中数组的值，比如数组中包含了名字，学籍等信息，特征就是这些信息。
向量：一条样本数据就是以一个向量的形式输入模型中的。如下所示。
[特征X1值，特征X2值，... ，特征Xn值，Y1值]
矩阵：将矩阵看成由向量组成的数组，形式上非常接近二维数组，前面说的数据集，通常就是以矩阵的形式输入模型中，如下所示。
[[特征X1值，特征X2值，... ，特征Xn值，Y1值]，
[特征X1值，特征X2值，... ，特征Xn值，Y2值]，
...
[特征X1值，特征X2值，... ，特征Xn值，Yn值]]
常用函数有两个：
①假设函数(Hypothesis Function)：机器学习的模型训练要依赖数据，通过将数据“喂”给假设函数，然后就会返回一个结果，这个结果是机器学习所得到的预测结果。通常假设函数写法H(x)，其中的x就是前面说的矩阵形式的数据。
②损失函数(Loss Function)：机器学习的训练并非一次成功的，而是不断学习，不断逼近学习目标的迭代过程，而帮助来衡量当前距离目标是逼近还是远离，我们就需要到损失函数。通常损失函数的写法L(x)。其中的x是假设函数的预测结果。损失函数的返回值越大，表示结果偏差越大。
成本函数(Cost Function)：与损失函数意义接近，同样是函数返回值越大，表示偏差越大。通常用J(x)表示，其中的x也是假设函数的预测结果。
区别成本函数和损失函数，关键看两者的对象。损失函数针对单个样本，成本函数针对整个数据集。也就是损失函数求得的 总和/平均值 就是成本函数。
举个例子，假设有10个样本，利用假设函数逐一预测后，通过损失函数逐一计算偏差。而总体偏差需要用到成本函数，成本函数由损失函数计算得到。实际计算中，可以令成本函数为损失函数值的总和，也可以是损失函数值的平均，最终目的，无非是希望最小化成本，也就是假设函数的预测正确率提高。
总结一下，训练过程中：
第一步：每个样本用损失函数计算后，各自得到一个损失值，损失值总和就是成本函数的损失值；
第二步：将成本函数的损失值作为优化方法的输入，完成对假设函数的参数调整；
第三步：继续重复第一步，计算出新的损失值，再重复第二步，调整假设函数的参数。
1. 5 机器学习的基本模式和优化方法
机器学习算法看似千差万别，但拆开比较，肯定少不了假设函数和损失函数这对固定组合。
要进行机器学习，至少需要三件东西：首先要准备数据，通过将数据“喂”给机器学习算法，进行训练；接着是假设函数，该函数接收“喂”进来的数据，然后“吐”出一个预测结果；最后是损失函数，因为一开始假设函数的预测结果很不可靠，而到底预测结果有多不可靠，需要靠损失函数来衡量，假设函数的预测结果“喂”给损失函数后，同样也会“吐”出一个结果，通常是数值形式，告知我们预测结果与真实情况到底差多少。
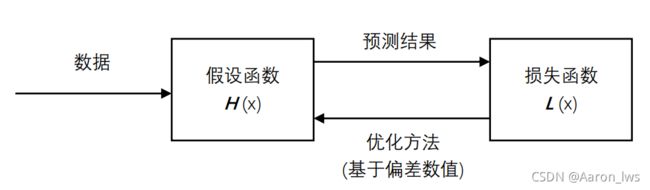
假设函数和损失函数是不断驱动机器学习模型不断朝着损失值最小化的方向逼近，最终实现拟合，完成学习任务。下图是一轮的学习过程。
图 1-2 假设函数产生的偏差驱动着机器学习模型不断优化
上面讲到，损失函数会计算出一个结果，来衡量预测结果与真实情况的偏差程度，但需要告诉假设函数去如何改正，最终能够对输入的数据产生期望的输出，这也是我们的最终目的，这个时候需要用到优化方法。优化方法的目的，就是通过调整假设函数的参数，令损失函数的损失值降到最小。可以看作min(L(x))函数。
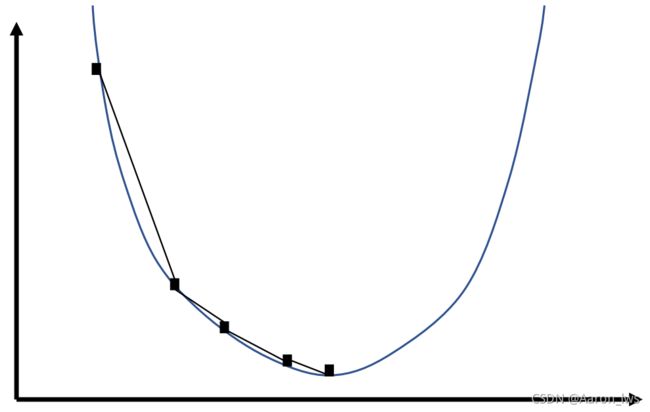
梯度下降法是机器学习中常用的一种优化方法。简单介绍来说，某个函数在某点的梯度指向该函数取得最大值的方向，那么它的反方向自然就是取得最小值的方向，所以只要让假设函数朝着梯度的负方向更新权值，就达到令损失函数的损失值最小化的效果。如下图所示。（涉及微积分学的相关知识，这里只是简单介绍一下，后续可能会专门写一篇博客来详细介绍这个方法。）
图1-3 梯度下降法的简单图表示
如果样本数量庞大，完成一次完整的梯度下降需要耗费很长时间，在实际训练中，会根据情况调整每次参与损失值计算的样本数量。每次迭代使用全部样本的，称为批量梯度下降；每次迭代只用一个样本的，称为随机梯度下降。随机梯度下降因为需要计算的样本小，所以迭代速度快，但容易陷入局部最优，而无法达到全局最优点。
1. 6 机器学习问题分类
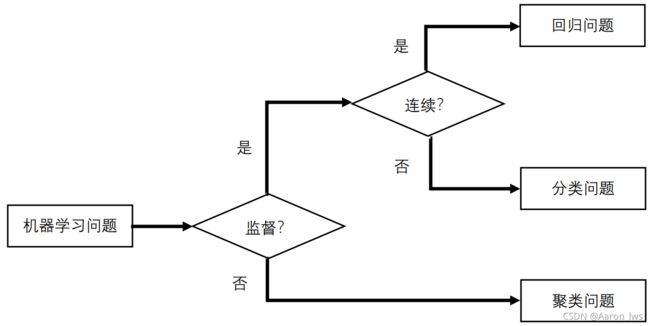
机器学习可以应用到多个领域，主要问题可以归纳为以下几类：
图1-4 机器学习问题具体类别的判断方法图
首先，根据是否有监督，分为：无监督学习(Unsupervised Learning)和有监督学习(Supervised Learning)。监督一词，具体来说，就是数据集中是否包含了预测结果。比如现在要做一个猫狗二分类的问题，在两个数据集中，标注出哪些图片是猫的标签，其余图片是狗的标签，这就是有监督学习，而无监督学习相反。
1. 7 机器学习算法的性能衡量指标
分类问题中，将机器学习模型的预测与实际情况比对后，结果可分为如下四种：
（第一个字母T/F，表示预测结果是否符合事实，模型猜的对不对；第二个字母P/N，表示预测的结果。）
- TP: True Positive，预测结果为正类，与事实相符，即事实为正类。
- TN: True Negative，预测结果为负类，与事实相符，即事实为负类。
- FP: False Positive，预测结果为负类，与事实不符，即事实为负类。
- FN: False Negative，预测结果为负类，与事实不符，即事实为正类。
常用指标如下:
- 准确率(Accuracy)：
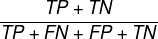(表示模型猜对的结果在全部结果的占比） - 精确率(Precision)【查准率】：
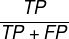(模型预测对正类结果的预测准确率) - 召回率(Recall)【查全率】：
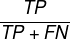(在全部正类中，看看模型能正确找出多少，找出越多，查全率越高)
1. 8 数据对算法结果的影响
①数据决定了算法能力的上限，而算法只是逼近这个上限。
②特征工程：机器学习模型从数据中的特征进行学习，选取的特征越合适，最后学习到的结果也越有价值。
写在最后：
最近除了看这本书，还借阅《python机器学习基础教程》和《机器学习实战：基于Scikit-Learn、Keras和TensorFlow》第二版。目前也同步在学习，后续也会写这两本的学习笔记，强推第二本，实战性强，适合新手入门，该系列书籍都不错。
本书第二章内容主要涉及介绍python，以及安装和基本用法，还有Numpy、Scikit-Learn简介和安装，基本上简介的篇幅很少，故跳过第二章，下一次推第三章的学习笔记。
图1-5 图书推荐