1. 题目描述
N 个有序整数数列已放在一维数组中,利用二分查找法查找整数 m 在数组中的位置。
若找到,则输出其下标值;反之,则输出 “ Not be found!”。
2. 问题分析
二分查找法(也叫折半查找)其本质是分治算法的一种。
所谓分治算法是指的分而治之,即将较大规模的问题分解成几个较小规模的问题,这些子问题互相独立且与原问题相同,通过对较小规模问题的求解达到对整个问题的求解。
我们把将问题分解成两个较小问题求解的分治方法称为二分法。需要注意的是,二分查找法只适用于有序序列。
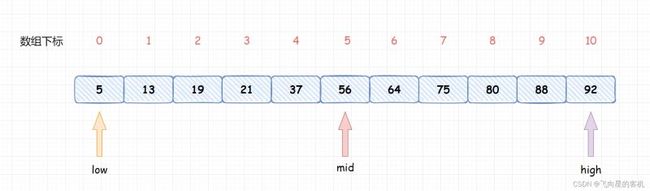
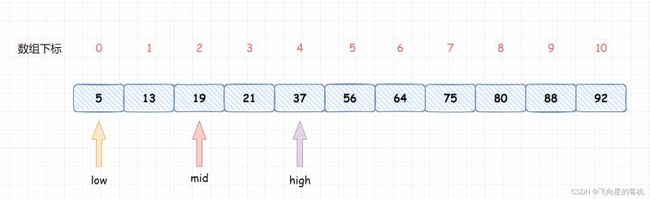
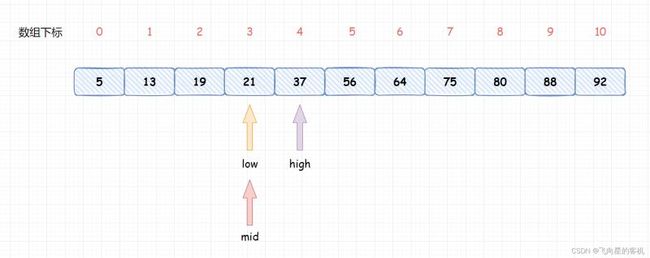
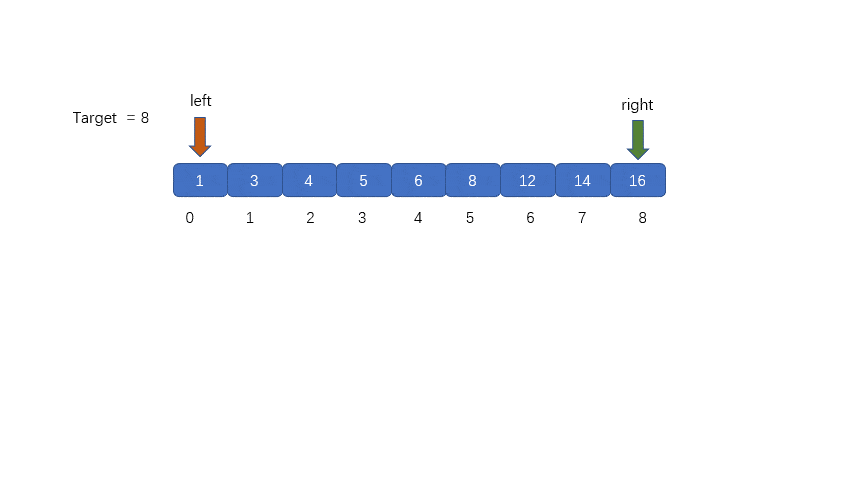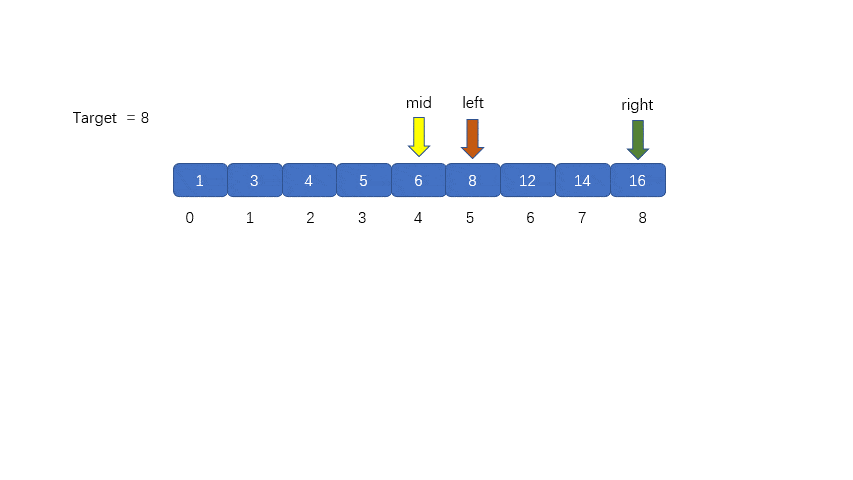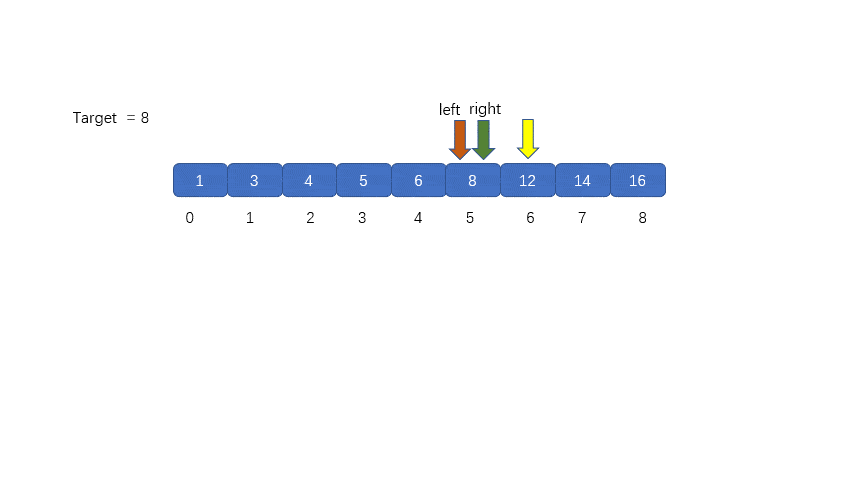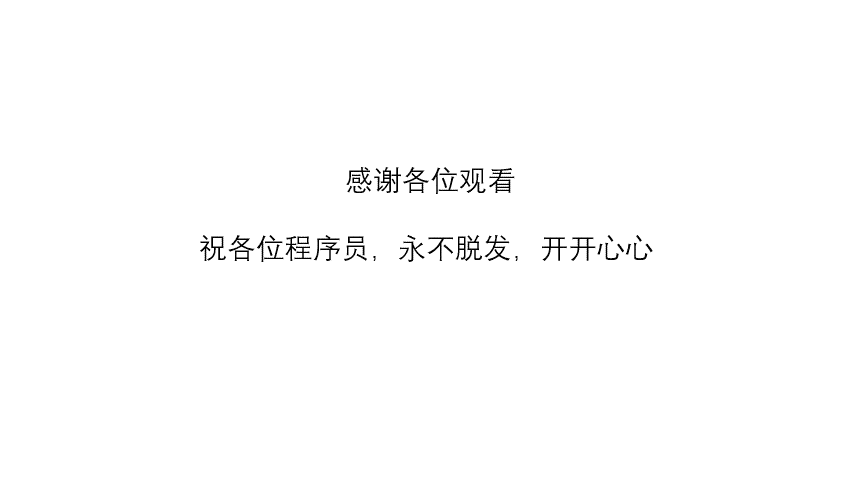
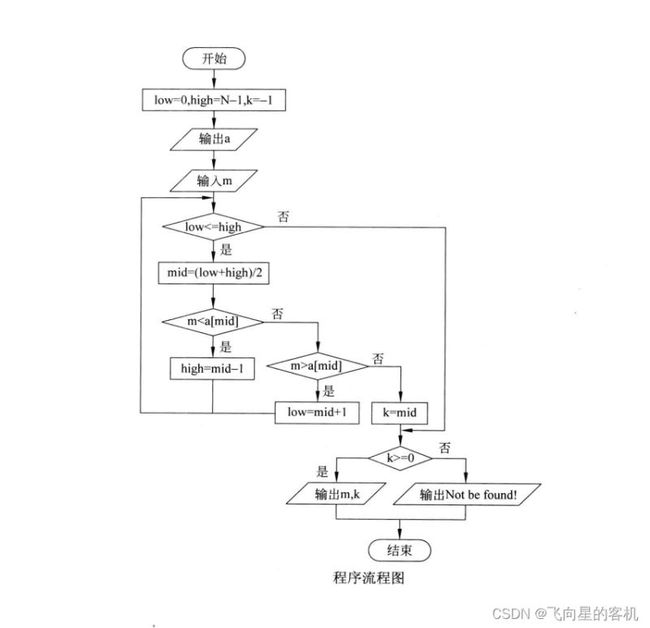
二分查找的基本思想是:每次查找前先确定数组中待查的范围,假设指针 low 和 high (low 如果m的值大于中间位置元素中的值,则下一次的查找范围放在中间位置之后的元素中; 反之,下一次的查找范围放在中间位置之前的元素中。直到 low>high,查找结束。 N 个有序数应存放在数组中,根据数组下标的取值范围知指针 low 和 high 的初值分别为 0、N-1。 除了三个指针变量 low、high、mid 之外还需要一个变量(假设为 k)来 记录下标,利用变量 k 的值来 判断整数是否在所给出的数组中。下面我们用示意图来表示二分查找的过程。 假设一维数组中存储的有序数列为:5 13 19 21 37 56 64 75 80 88 92,要查找的整数 m 为 21。 根据二分查找方法可知指针 low 和 high 最初分别指向元素 5 和 92,由 mid=(low+high)/2 知,指针 mid 指向元素 56。示意图如下: 变量 m 所代表的整数 21 与 指针 mid 所指的元素 56 进行比较, 21 小于 56, 根据二分查找算法知, 查找范围现在缩小到指针 mid 所指元素的前面, 即从 5~37 的范围。 指针 high 原来指向下标为 N-1 的元素,现在指向下标为 mid-1 的元素,接着重新计算指针 mid 所指元素的下标。 再次进行比较,21 大于 19,现在比较范围再次转移到 mid 所指元素的后面,low 元素所指元素下标由 0 变为 mid+1。 当前 mid 所指元素的值为 21,与要查找的整数值相同,因此查找成功,所查元素在表中序号等于指针 mid 的值。 动图解析 流程图设计 完整代码 运行结果 代码贴图 程序分析 在上述程序中循环结束可以有两种情况。 一种是由于循环的判定条件 low <= high 不成立的情况下跳出循环,此时可知查找不成功。 在查找不成功的情况下,语句 else {k=mid; break;} 是不执行的,所以变量 k 的值不变仍为初值 -1。 第二种结束循环的情况是由于执行了 break; 语句而跳出循环,在此情况下,变量 k 的值由 -1 变成了一个大于等于 0 的数,即指针 mid 所指元素的下标值。 所以在最后用选择结构来判定 k 的值,从而确定整个查找过程是否成功。 continue 语句的格式为: continue 语句用于循环语句(while循环语句 或 do...while循环语句 或 for循环语句)中,作为循环体的一部分。 在程序执行时,一旦遇到了 continue 语句,则立即结束本次循环,即跳过循环体中 continue 后面尚未执行的语句,接着进行是否继续循环的条件判定。 break 语句的格式如下: break 语句 可用在 switch 语句中。 在程序执行时, 一旦遇到了 break 语句, 则立即退出当前的 switch 语句。 除此之外, break 语句还能用于循环语句(while循环语句 或 do...while 循环语句 或 for 循环语句))中, 作为循环体的一部分。 在程序执行时, 一旦遇到了 break语句, 则立即退出当前的循环体,接着执行当前循环体下面的语句。 continue 只是结束本次循环,不再执行循环体中 continue 后面的其余语句,并不是终止当前循环。 break 是直接终止当前的循环。 在一个给定的数据结构中查找某个指定的元素,通常根据不同的数据结构,应采用不同的查找方法。对于一个有序数列,除了采用二分查找法之外还可以采用 顺序查找 的方法。 顺序查找一般是指 在线性表中查找指定的元素,其基本方法如下: 从线性表的第一个元素开始,依次将线性表的元素与被查元素进行比较,若相等则表示找到即查找成功; 若线性表中所有的元素都与被查元素进行了比较但都不相等,则表示线性表中没有要找的元素即查找失败。 在长度为 n 的线性表中查找指定元素,最好的情况是比较一次成功,最坏的情况是比较 n 次,平均要比较(1+2+3+⋅⋅⋅+n)/n=(1+n)/2 次。 尽管顺序查找的效率低,但对于一些情况只能采用顺序查找的方法,如对于一个无序表进行查找。 完整代码 运行结果 到此这篇关于C语言算法练习之折半查找的实现的文章就介绍到这了,更多相关C语言折半查找内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!3. 算法设计
4. 动图演示
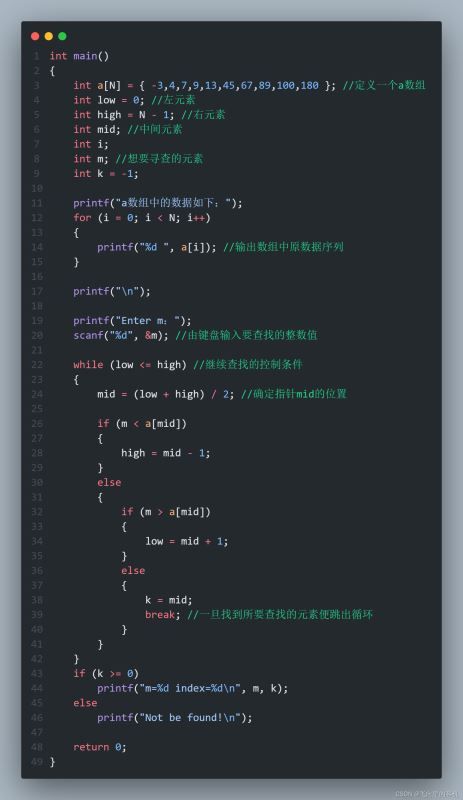
5. 代码实现
#include
6.知识点补充
continue 语句
continue;break 语句
break;continue语句 和 break语句的区别
7. 问题拓展
#include