数据结构－图

目录

图的概念

图的存储结构

邻接矩阵

邻接表

---

图的概念

图是由集合Ｖ和集合Ｅ组成。记为Ｇ＝（Ｖ，Ｅ）。集合Ｖ是顶点的有穷非空集合，Ｅ是Ｖ中顶点偶对的有穷集合，这些顶点偶对称为边。Ｅ（Ｇ）可以为空集，Ｖ（Ｇ）不为空。

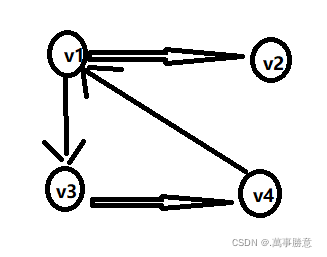
若边集Ｅ为有向边的集合，则称该图为有向图，反之为无向图。

在有向图中，用＜＞表示顶点对，两顶点的边是有方向的，有向图中的边也称为弧；在无向图中，用（）表示顶点对。

                  有向图　　                                                无向图

完全图：
        对于无向图，若具有ｎ（ｎ－１）／２条边，则称为无向完全图，对于有向图，若具有ｎ（ｎ－１）条边，则称为有向完全图。

权和网：
        每条边可以标上具有某种意义的数值，该数值称为权值，具有权的图称为网。

度：
        顶点ｖ的度是指和ｖ有关联的边的数目。对于有向图，顶点的度分为入度和出度，入度是指以该顶点为终点的边数，出度为以该顶点为始边的边的数目。

路径长度：路径长度是指一条路径上经过的边或弧的数目。

回路或环：

        第一个顶点和最后一个顶点相同的路径称为回路或环。

简单路径，简单回路，简单环：

        序列中顶点不重复出现的路径称为简单路径。除第一个和最后一个顶点外，其余顶点不重复出现的回路，称为简单回路或简单环。

图的存储结构

邻接矩阵

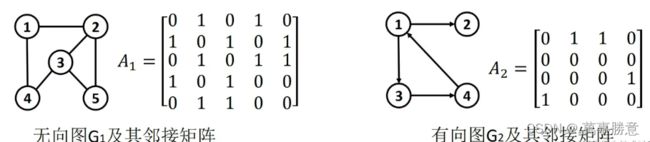
邻接矩阵是表示顶点之间相邻关系的矩阵。图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

 结点数为n的图G的邻接矩阵A是n×n。占用ｎ＾２个空间

一般，图中以０代表无边， １代表有边。
           网中有边写权值，无边记为∞

注意：

无向图的邻接矩阵是对称矩阵，对规模较大的邻接矩阵可使用压缩存储
邻接矩阵表示法的空间复杂度是O(2),其中n为图的顶点数对无向图，邻接矩阵的第i行（或第i列）非零元素（或非∞元素）的个数,正好是第i个顶点的TD()
对有向图，邻接矩阵的第i行（或第i列）非零元素（或非∞元素）的个数,正好是第i个顶点的出度OD()（或入度ID()）
邻接矩阵法存储图，确定图中任意两个顶点之间是否有边相连只需O(1)时间复杂度
但要确定图中有多少条边，则必须遍历整个二维数组，时间复杂度为O(2)
稠密图适合使用邻接矩阵的存储表示

存储结构：

#define MaxInt 32767                    	//表示极大值，即∞
#define MVNum 100                       	//最大顶点数
#define OK 1	
 						
typedef char VerTexType;              		//假设顶点的数据类型为字符型 
typedef int ArcType;                  		//假设边的权值类型为整型 

//- - - - -图的邻接矩阵存储表示- - - - -
typedef struct{ 
	VerTexType vexs[MVNum];            		//顶点表 
	ArcType arcs[MVNum][MVNum];      		//邻接矩阵 
	int vexnum,arcnum;                		//图的当前点数和边数 
}AMGraph;

                                                           图的邻接矩阵存储表示

创建无向网：

１.输入总顶点数和边数

２.依次输入各个顶点的信息并将其存入顶点表中

３.初始化邻接矩阵，使每个权值初始化为极大值

４.构造邻接矩阵，依次输入每条边依附的顶点和其权值，确定两个顶点在图中的位置后，使边赋予相应的权值。

int LocateVex(AMGraph G , VerTexType v){
	//确定点v在G中的位置
	for(int i = 0; i < G.vexnum; ++i)
		if(G.vexs[i] == v)
			return i;
   return -1;
}//LocateVex

int CreateUDN(AMGraph &G){ 
    //采用邻接矩阵表示法，创建无向网G 
	int i , j , k;
	cout <<"请输入总顶点数，总边数，以空格隔开：";
    cin >> G.vexnum >> G.arcnum;							//输入总顶点数，总边数
	cout << endl;

	cout << "输入点的名称，如a" << endl;

    for(i = 0; i < G.vexnum; ++i){   
		cout << "请输入第" << (i+1) << "个点的名称:";
		cin >> G.vexs[i];                        			//依次输入点的信息 
	}
	cout << endl;
    for(i = 0; i < G.vexnum; ++i)                			//初始化邻接矩阵，边的权值均置为极大值MaxInt 
		for(j = 0; j < G.vexnum; ++j)   
			G.arcs[i][j] = MaxInt;  
	cout << "输入边依附的顶点及权值，如 a b 5" << endl;
	for(k = 0; k < G.arcnum;++k){							//构造邻接矩阵 
		VerTexType v1 , v2;
		ArcType w;
		cout << "请输入第" << (k + 1) << "条边依附的顶点及权值:";
		cin >> v1 >> v2 >> w;								//输入一条边依附的顶点及权值
		i = LocateVex(G, v1);  j = LocateVex(G, v2);		//确定v1和v2在G中的位置，即顶点数组的下标 
		G.arcs[i][j] = w;									//边的权值置为w 
		G.arcs[j][i] = G.arcs[i][j];						//置的对称边的权值为w 
	}//for	
	return OK; 
}//CreateUDN 

                                             　采用邻接矩阵表示法创建无向网

邻接矩阵表示法的优缺点：

优点：

        １便于判断两个顶点是否有边。
        ２便于计算各个顶点的度

缺点：

        １不便于增加和删除顶点
        ２不便于统计边的数目
        ３空间复杂度高

邻接表

邻接表是图的一种链式存储结构。建立邻接表的时间复杂度为O(n+e)。

在有向图的邻接表中，第i个单链表链接的边都是顶点i发出的边。

为了求第i个顶点的入度，需要遍历整个邻接表。因此可以建立逆邻接表。在有向图的逆邻接表中，第i个单链表链接的边都是进入顶点i的边。

设图中有n个顶点，e条边，则用邻接表表示无向图时，需要n个顶点结点，2e个表结点；用邻接表表示有向图时，若不考虑逆邻接表，只需n个顶点结点，e个边结点。

对于无向图，邻接矩阵的第i行（或第i列）非零元素（或非∞元素）的个数正好是第i个顶点的度TD(vi)。

对于有向图，邻接矩阵的第i行（或第i列）非零元素（或非∞元素）的个数正好是第i个顶点的出度OD(vi)（或入度ID(vi)）。

图的邻接表存储结构

#define MVNum 100                        	//最大顶点数 
#define OK 1

typedef char VerTexType;					//顶点信息
typedef int OtherInfo;						//和边相关的信息 

//- - - - -图的邻接表存储表示- - - - - 
typedef struct ArcNode{                		//边结点 
    int adjvex;                          	//该边所指向的顶点的位置 
    struct ArcNode *nextarc;          		//指向下一条边的指针 
    OtherInfo info;                      	//和边相关的信息 
}ArcNode; 

typedef struct VNode{ 
    VerTexType data;                    	//顶点信息 
    ArcNode *firstarc;                		//指向第一条依附该顶点的边的指针 
}VNode, AdjList[MVNum];               		//AdjList表示邻接表类型 

typedef struct{ 
    AdjList vertices;                 		//邻接表 
    int vexnum, arcnum;              		//图的当前顶点数和边数 
}ALGraph;

                                                                图的邻接表存储表示

邻接表创建无向图

1　输入总顶点数和边数
２　依次输入顶点的信息存入顶点表中，使每个表头节点的指针域初始化为ＮＵＬＬ
 3　创建邻接表。依次输入每条边依附的两个顶点，确定顶点位置之后，将边节点分别插入两个边链表的头部

int LocateVex(ALGraph G , VerTexType v){
	//确定点v在G中的位置
	for(int i = 0; i < G.vexnum; ++i)
		if(G.vertices[i].data == v)
			return i;
   return -1;
}//LocateVex

int CreateUDG(ALGraph &G){ 
	//采用邻接表表示法，创建无向图G
	int i , k;

	cout <<"请输入总顶点数，总边数中间以空格隔开:";
	cin >> G.vexnum >> G.arcnum;				//输入总顶点数，总边数 
    cout << endl;
	
	cout << "输入点的名称，如 a " <> G.vertices[i].data;           	//输入顶点值 
		G.vertices[i].firstarc=NULL;			//初始化表头结点的指针域为NULL 
    }//for
	cout << endl;
    
	cout << "请输入一条边依附的顶点,如 a b" << endl;
	for(k = 0; k < G.arcnum;++k){        		//输入各边，构造邻接表
		VerTexType v1 , v2;
		int i , j;
		cout << "请输入第" << (k + 1) << "条边依附的顶点:";
		cin >> v1 >> v2;                 		//输入一条边依附的两个顶点
		i = LocateVex(G, v1);  j = LocateVex(G, v2);
		//确定v1和v2在G中位置，即顶点在G.vertices中的序号 

		ArcNode *p1=new ArcNode;               	//生成一个新的边结点*p1 
		p1->adjvex=j;                   		//邻接点序号为j 
		p1->nextarc= G.vertices[i].firstarc;  G.vertices[i].firstarc=p1;  
		//将新结点*p1插入顶点vi的边表头部

		ArcNode *p2=new ArcNode;                //生成另一个对称的新的边结点*p2 
		p2->adjvex=i;                   		//邻接点序号为i 
		p2->nextarc= G.vertices[j].firstarc;  G.vertices[j].firstarc=p2;  
		//将新结点*p2插入顶点vj的边表头部 
    }//for 
    return OK; 
}//CreateUDG

                                                         采用邻接表表示法创建无向图

优缺点：

优点：方便找任一顶点的所有“邻接点”节约稀疏图的空间：需要N个头指针+2E个结点(每个结点至少2个域)对无向图而言，方便计算任一顶点的度。

缺点：对有向图而言，只能计算“出度”，需要构造“逆邻接表”来方便计算“入度”。