动态规划入门攻略(一)

目录

什么是动态规划？

零钱兑换 

不同路径  

跳跃游戏 

不同路径II 

粉刷房子 

 解码方法

最长连续递增序列 

最小路径和 

空间优化  ——  滚动数组

比特位计数 

---

什么是动态规划？

定义：

动态规划是分治思想的延伸，通俗一点来说就是大事化小，小事化无的艺术。

在将大问题化解为小问题的分治过程中，保存对这些小问题已经处理好的结果，并供后面处理更大规模的问题时直接

使用这些结果。

动态规划具备了以下三个特点：

1. 把原来的问题分解成了几个 相似的子问题 。

2. 所有的子问题都 只需要解决一次 。

3. 储存 子问题的解。

动态规划的本质，是对问题状态的定义和状态转移方程的定义(状态以及状态之间的递推关系)

动态规划问题一般从以下四个角度考虑：

1. 状态定义

状态在动态规划种的作用属于定海神针

简单地说，解动态规划的时候需要开一个数组，数组的每个元素f[i]或者f[i][j]代表什么

    -类似于解数学题，X,Y,Z代表什么

确定状态需要两个意识：

    -最后一步

    -子问题

2. 状态间的转移方程定义

3. 状态的初始化

初始条件：用状态转移方程算不出来，需要手工定义！

边界条件：保证数组不能越界

4. 返回结果

状态定义的要求： 定义的状态一定要形成递推关系 。

一句话概括：三特点四要素两本质

适用场景：最大值 / 最小值 , 可不可行 , 是不是，方案个数

动态规划题目特点：

1.计数

    -有多少种方式走到右下角

    -有多少种方法选出k个数使得和是Sum

2.求最大最小值

    -从左上角走到右下角路径的最大数字和

    -最长上升子序列长度

3.求存在性

    -取石子游戏，先手是否必胜

    -能不能选出k个数使得和是Sum

零钱兑换 

322. 零钱兑换(求最值型动态规划)  -------- 简单题目理解动态规划的概念

动态规划组成部分一：确定状态

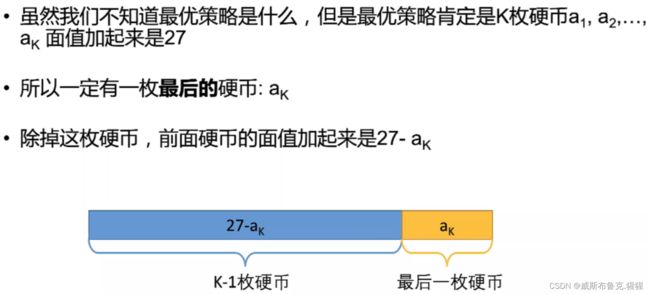
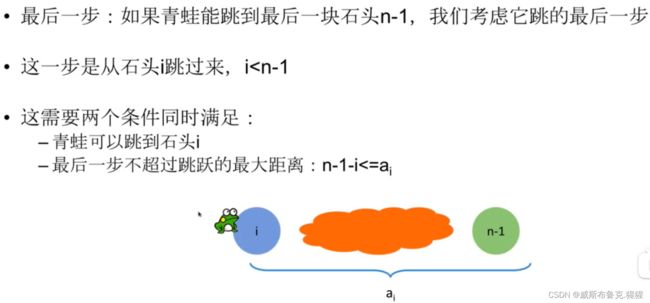
最后一步

最后一步的两个关键点：

 子问题： 

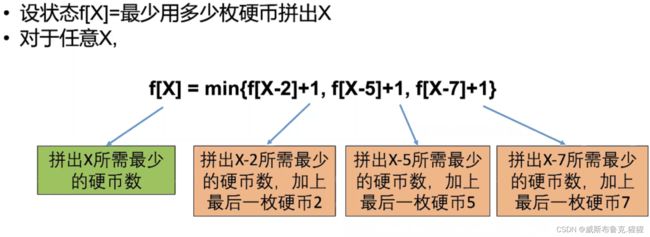
 动态规划组成部分二：转移方程 

动态规划组成部分三：初始条件和边界情况 

初始条件：用状态转移方程算不出来，需要手工定义！

边界条件：保证数组不能越界

动态规划组成部分四：计算顺序

public int coinChange(int[] coins, int amount) {
        int[] f = new int[amount + 1];
        int n = coins.length;
        //初始化条件
        f[0]= 0;
        for(int i = 1;i <= amount;i++){
            f[i] = Integer.MAX_VALUE;//设置为coins[i]不可达
            //最后一个硬币A[j]
            for(int j = 0;j < n;j++){
//                //i >= coins[j]：防止负数的出现(如果要拼3块钱,就不可能出现5块钱的硬币)
//                //拼不出要的那种方案
//                if(i >= coins[j] && f[i - coins[j]] != Integer.MAX_VALUE){
//                    //状态转移方程
//                    f[i] = Math.min(f[i - coins[j]] + 1,f[i]);
//                }
                if(i >= coins[j] && f[i - coins[j]] != Integer.MAX_VALUE && f[i - coins[j]] + 1 < f[i]){
                    f[i] = f[i - coins[j]] + 1;
                }
            }
        }
        if(f[amount] == Integer.MAX_VALUE){
            f[amount] = -1;
        }
        return f[amount];
    }

不同路径 

62. 不同路径 ----- 计数型动态规划

动态规划组成部分一：确定状态

最后一步：

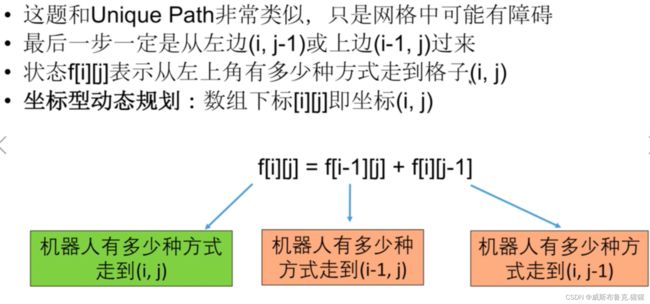
无论机器人用何种方式到达右下角，总有最后挪动的一步：——向右或向下右下角坐标设为(m - 1,n - 1)；那么前一步机器人一定是在(m - 2,n - 1)或(m - 1,n - 2)

子问题

那么，如果机器人有X中方式从左上角走到(m - 2,n - 1),有Y种方式从左上角走到(m - 1,n - 2),则机器人有X + Y种方式走到(m - 1,n - 1)

问题转化为，机器人有多少种方式从左上角走到(m - 2,n - 1)和(m - 1,n - 2)

原题要求有多少种方式从左上角走到(m - 1,n - 1)

注：因为X种从左上角走到(m - 2,n - 1)的方式和Y种从左上角走到(m - 1,n - 2)的方式两者互不相干，所以可以相加

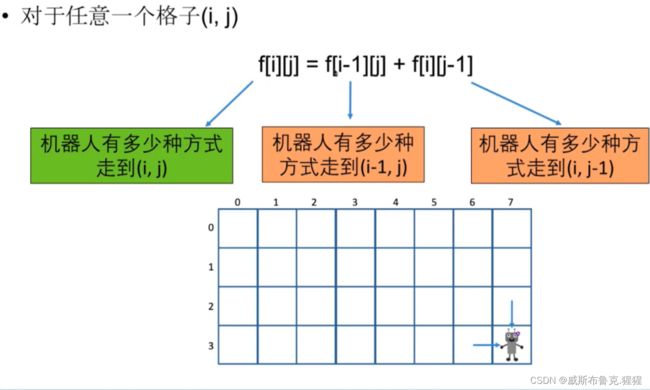
动态规划组成部分二：转移方程

状态：设f[i][j]为机器人有多少种方式从左上角走到(i,j)

动态规划组成部分三：初始条件和边界情况 

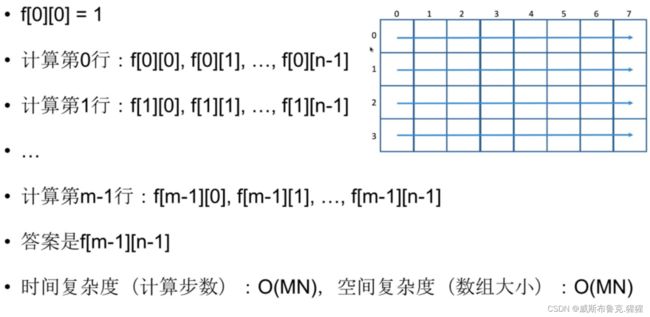
动态规划组成部分四：计算顺序 

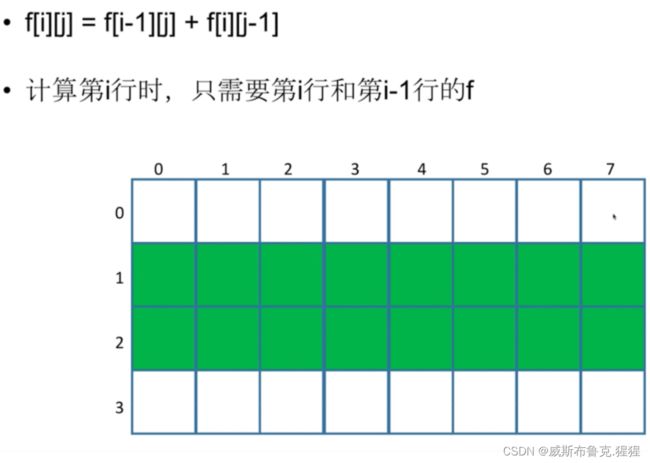
二维的一般按照一行一行的方式去计算，完了在每一行中再去计算每一列；因为这样(对于此题而言)，计算某个坐标时，它的左和上已经计算完了，所以动态规划的方程就能更快。

    /**
     * @return 时间复杂度(计算步数)：O(MN),空间复杂度(数组大小)：O(MN)
     */
    public int uniquePaths(int m, int n) {
        int[][] f = new int[m][n];
        //一行一行的去计算
        for(int i = 0;i < m;i++){
            //每一行再去计算列
            for(int j = 0;j < n;j++){
                //边界条件
                if(i == 0 || j == 0){
                    f[i][j] = 1;
                }else{
                    //             up           left
                    f[i][j] = f[i - 1][j] + f[i][j - 1];
                }
            }
        }
        return f[m - 1][n - 1];
    }

跳跃游戏 

55. 跳跃游戏 ------   存在型动态规划55. 跳跃游戏 ------

动态规划组成部分一：确定状态

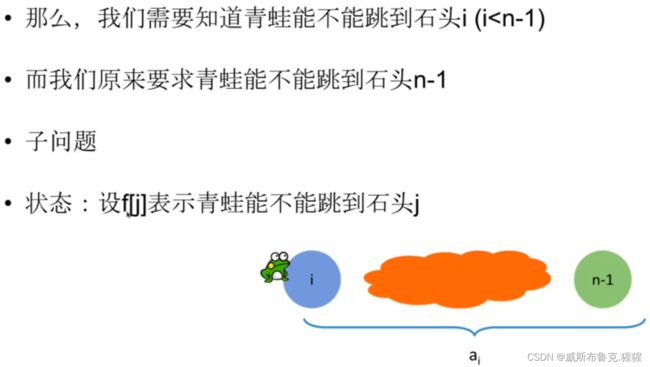
子问题 

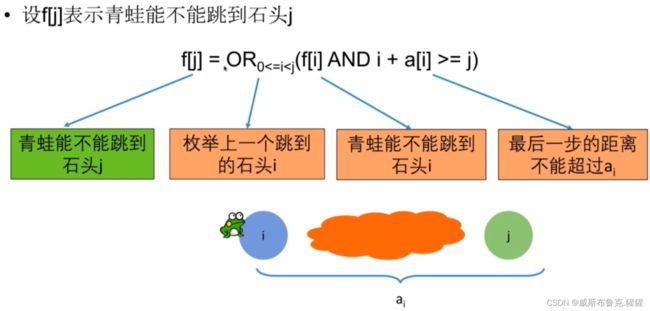
动态规划组成部分二：转移方程 

0 ~ i的任意一个石头能够满足跳到石头j即符合条件

动态规划组成部分三：初始条件和边界情况 

这道题没啥特殊的边界条件

设f[j]表示青蛙能不能跳到石头j

初始条件：f[0] = True,因为青蛙一开始就在石头0

动态规划组成部分四：计算顺序

动态规划最重要的突破口：研究最优策略的最后一步 

    /**
     * @return 时间复杂度：O(N^2)，空间复杂度(数组大小)：O(N)
     */
    public boolean canJump(int[] nums) {
        if(nums.length == 0){
            return false;
        }
        int n = nums.length;
        boolean[] f = new boolean[n];
        //初始条件
        f[0] = true;
        for(int i = 1;i < n;i++){
            //规划最后一块石头之前的石头的跳法
            f[i] = false;//如果0 ~ i(倒数第二个石头)个石头中,有任意一个可以跳到最后一块石头,则置为true
            for(int j = 0;j < i;j++){
                if(f[j] && j + nums[j] >= i){
                    f[i] = true;
                    break;//如果某个石头可以跳到最后一个石头,就可以退出来了
                }
            }
        }
        return f[n - 1];
    }

不同路径II 

63. 不同路径 II --------坐标型动态规划

坐标型动态规划总结

动态规划组成部分一：确定状态

动态规划组成部分二：转移方程 

和不同路径是一样的

初始条件和边界情况 

    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        if(m == 0){
            return 0;
        }
        int n = obstacleGrid[0].length;
        if(n == 0){
            return 0;
        }
        int[][] f = new int[m][n];
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(obstacleGrid[i][j] == 1){
                    f[i][j] = 0;
                }else{
                    //初始化条件
                    if(i == 0 && j == 0){
                        f[i][j] = 1;
                    }else{
                        //if(i == 0) f[i][j] = f[i][j - 1];这样写有两行代码,复杂点
                        f[i][j] = 0;//为了同时处理第一行第一列,
                        if(i - 1 >= 0){
                            f[i][j] += f[i - 1][j];
                        }
                        if(j - 1 >= 0){
                            f[i][j] += f[i][j - 1];
                        }
                    }
                }
            }
        }
        return f[m - 1][n - 1];
    }

粉刷房子 

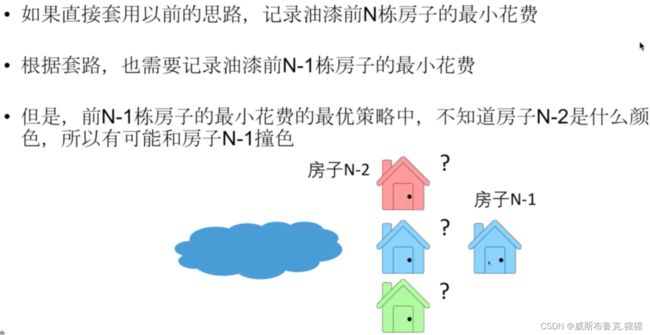
剑指 Offer II 091. 粉刷房子 ------  序列型动态规划 

动态规划组成部分一：确定状态 

 解决方式： 

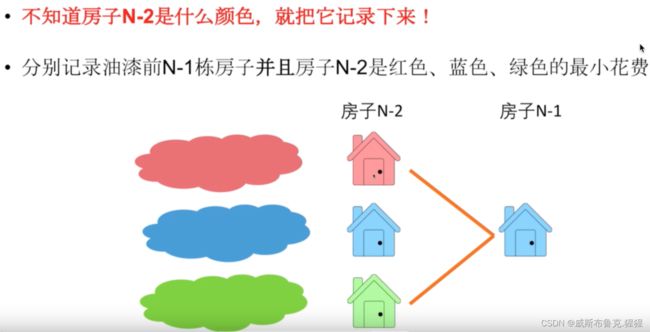
不知道房子N - 2是什么颜色，就把它记录下来！

注意点：

在坐标型动态规划的题目中，下标是从0开始的，所以nums[0]代表着一个问题的解

但是在序列型动态规划的问题中，虽然数组下标是从0开始的，但是处理的是nums[i]之前的问题的解，所以nums[0]不会代表一个问题的解；所以在序列型动态规划题目中，数组长度一般开N + 1

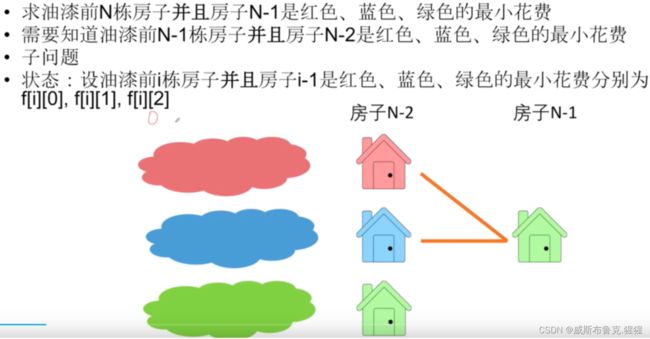
子问题：

动态规划组成部分二：转移方程 

动态规划组成部分三：初始条件和边界情况

动态规划组成部分四：计算顺序 

    public int minCost(int[][] costs) {
        int n = costs.length;
        if(n == 0){
            return 0;
        }
        int[][] f = new int[n + 1][3];//n个房子,开n + 1个数组长度
        //初始化条件
        f[0][0] = f[0][1] = f[0][2] = 0;
        for(int i = 1;i <= n;i++){
            //j是房子(i - 1)的颜色
            for(int j = 0;j < 3;j++){
                f[i][j] = Integer.MAX_VALUE;
                //k是房子(i - 2)的颜色
                for(int k = 0;k < 3;k++){
                    //不能撞色
                    if(j == k){
                        continue;
                    }
                    if(f[i - 1][k] + costs[i - 1][j] < f[i][j]){
                        f[i][j] = f[i - 1][k] + costs[i - 1][j];
                    }
                }
            }
        }
        int res = f[n][0];
        if(f[n][1] < res){
            res = f[n][1];
        }
        if(f[n][2] < res){
            res = f[n][2];
        }
        return res;
    }

 解码方法

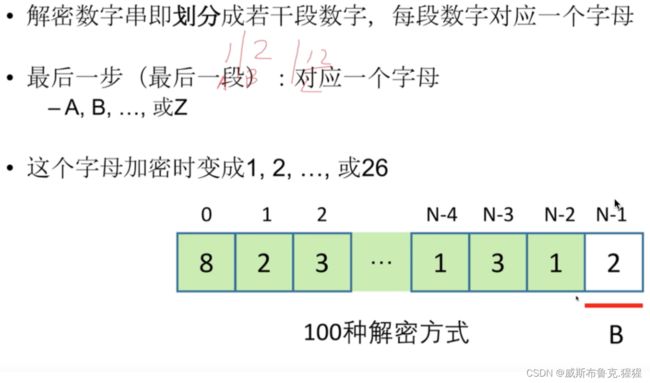
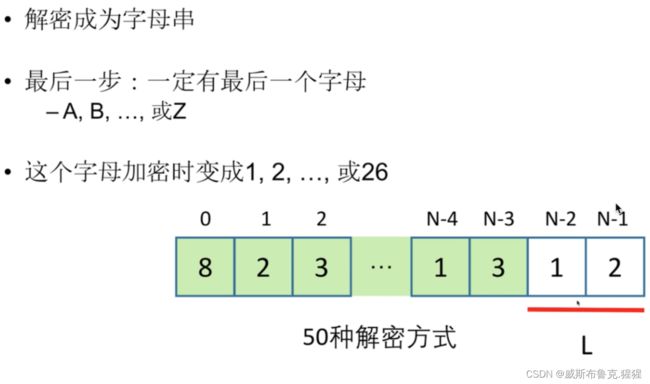
91. 解码方法 ----- 划分型动态规划

动态规划组成部分一：确定状态

最后一步

 

 子问题

动态规划组成部分二：转移方程 

动态规划组成部分三：初始条件和边界情况 

设数字串S前 i 个数字解密成字母串有f[i]种方式

初始条件：f[0] = 1，即空串有 1 种方式解密

        -解密成空串

边界情况：如果i = 1,只看最后一个数字 

动态规划组成部分四：计算顺序

f[0]，f[1]，...，f[N]

答案是f[N]

时间复杂度O(N)，空间复杂度O(N)

    public int numDecodings(String s) {
        //如果不变成数组,所有的(i - 1)要写成s.charAt(i - 1)
        char[] sc = s.toCharArray();
        int n = sc.length;
        if(n == 0){
            return 0;
        }
        //数组长度：n + 1(这样会很好处理)
        int[] f = new int[n + 1];
        f[0] = 1;
        //i: 前i个字母
        for(int i = 1;i <= n;i++){
            f[i] = 0;
            //last digit
            //前(i - 1)个字符的解码方式
            int t = sc[i - 1] - '0';
            if(t >= 1 && t <= 9){
                f[i] += f[i - 1];
            }
            //i的长度必须大于1
            if(i >= 2){
                //last two digits
                //前(i - 2)个字符的解码方式
                t = (sc[i - 2] - '0') * 10 + (sc[i - 1] - '0');
                if(t >= 10 && t <= 26){
                    f[i] += f[i - 2];
                }
            }
        }
        return f[n];
    }

最长连续递增序列 

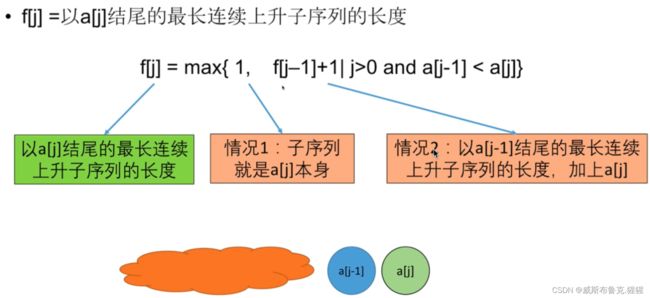
674. 最长连续递增序列 ----- 求最值型动态规划

动态规划组成部分一：确定状态

最后一步

子问题

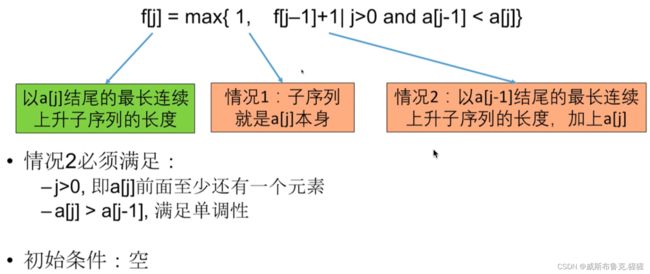
动态规划组成部分二：转移方程 

动态规划组成部分三：初始条件和边界情况

动态规划组成部分四：计算顺序

    int result = 0;
    public int findLengthOfLCIS(int[] nums) {
        int n = nums.length;
        if(n == 0){
            return 0;
        }
        calc(nums,n);
        return result;
    }
    private void calc(int[] nums,int n){
        int[] f = new int[n];
        for(int i = 0;i < n;i++){
            f[i] = 1;
            if(i > 0 && nums[i - 1] < nums[i]){
                f[i] = f[i - 1] + 1;
            }
            if(f[i] > result){
                result = f[i];
            }
        }
    }
    public int findLengthOfLCIS2(int[] nums) {
        //滚动数组优化空间复杂度为O(1)
        int n = nums.length;
        if(n == 0){
            return 0;
        }
        calc(nums,n);
        return result;
    }
    private void calc2(int[] nums,int n){
        int[] f = new int[2];
        int olds = 0;
        int news = 0;
        for(int i = 0;i < n;i++){
            olds = news;
            news = 1 - news;
            f[news] = 1;
            if(i > 0 && nums[i - 1] < nums[i]){
                f[news] = f[olds] + 1;
            }
            if(f[news] > result){
                result = f[news];
            }
        }
    }

最小路径和 

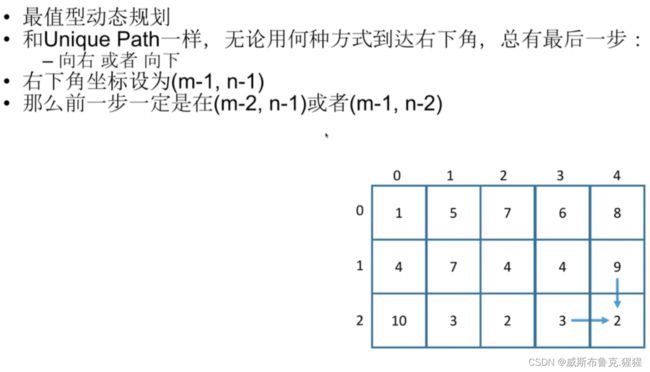
64. 最小路径和 ----- 求最值型动态规划

动态规划组成部分一：确定状态

最后一步

 子问题

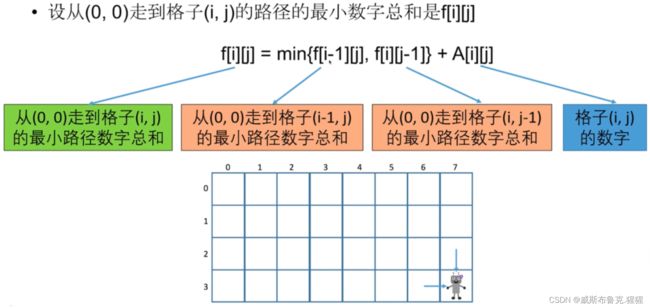
动态规划组成部分二：转移方程 

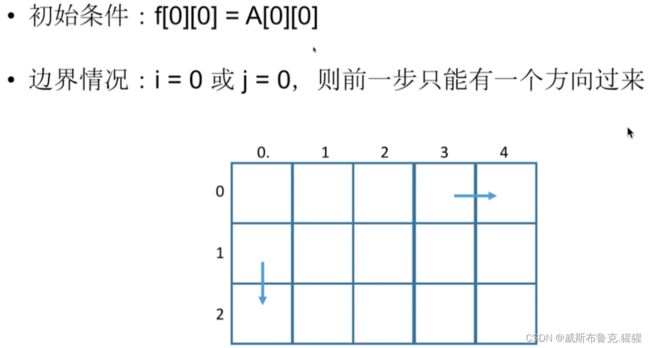
动态规划组成部分三：初始条件和边界情况

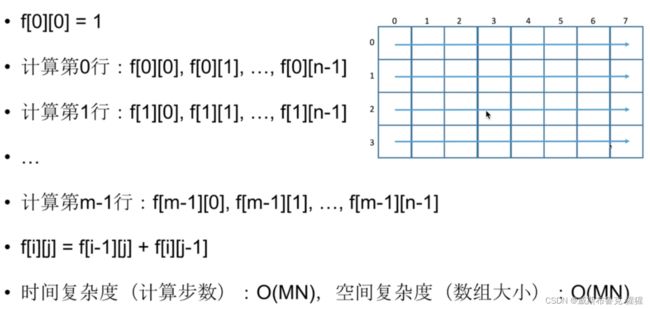
动态规划组成部分四：计算顺序

    public int minPathSum(int[][] grid) {
        if(grid.length == 0 || grid[0].length == 0){
            return 0;
        }
        int m = grid.length;
        int n = grid[0].length;
        int[][] f = new int[2][n];
        int old = 1,now = 0;
        int t1,t2;
        for(int i = 0;i < m;i++){
            old = now;//old是i - 1行
            now = 1 - now;//now 是 i 行
            //为啥now = 1 - now：  1 - 1 = 0;1 - 0 = 1实现滚动
            for(int j = 0;j < n;j++){
                if(i == 0 && j == 0){
                    f[now][j] = grid[i][j];
                    continue;
                }
                f[now][j] = grid[i][j];
                if(i > 0){
                    t1 = f[old][j];
                }else{
                    t1 = Integer.MAX_VALUE;
                }
                if(j > 0){
                    t2 = f[now][j - 1];
                }else{
                    t2 = Integer.MAX_VALUE;
                }
                if(t1 < t2){
                    f[now][j] += t1;
                }else{
                    f[now][j] += t2;
                }
            }
        }
        return f[now][n - 1];
    }

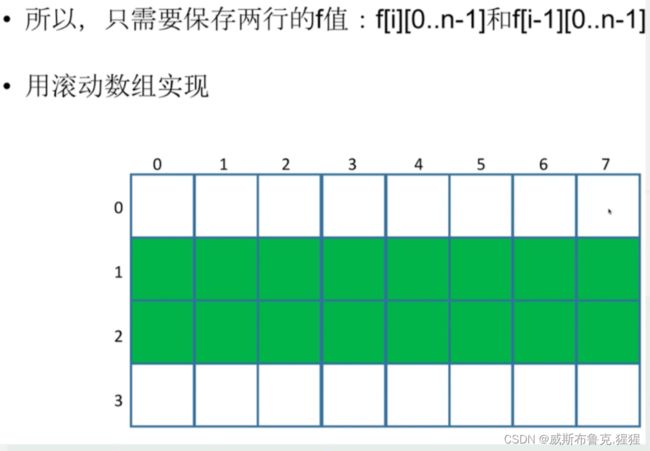
 空间优化  ——  滚动数组

   空间还是F(0)的空间，但是覆盖掉了原来的值 

比特位计数 

338. 比特位计数  -- 序列+位操作型动态规划

动态规划组成部分一：确定状态

最后一步

 子问题

动态规划组成部分二：转移方程 

动态规划组成部分三：初始条件和边界情况

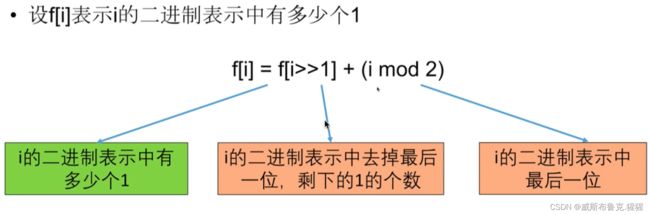
设 f[i] 表示 i 的二进制表示中有多少个1

f[i] = f[i >> 1] + (i % 2)

初始条件：f[0] = 0

动态规划组成部分四：计算顺序

f[0]，f[1]，f[2]，...，f[N]

时间复杂度O(N)

空间复杂度O(N)