AVL树笔记
文章目录
- AVL树
-
- 什么是AVL树?
-
- 要点
- 例子
- AVL树的结点
- AVL树的插入
-
- 插入过程
-
- 代码
- 例子
- 直线or折线
-
- 更新平衡因子的轨迹是直线
- 更新平衡因子的轨迹是折线
- 树的旋转
-
- 左单旋
-
- 抽象图
- 代码实现
- 右单旋
-
- 抽象图
- 代码实现
- 左右双旋
-
- 抽象图
- 代码实现
- 右左双旋
-
- 抽象图
- 代码实现
- 检验是否是AVL树
-
- 代码实现
- 总结
AVL树
什么是AVL树?
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。–百度百科
要点
- AVL树是二叉搜索树
- AVL在二叉搜索树的基础上加了平衡因子(bf),平衡因子=右子树的高度-左子树的高度,平衡因子用来调节高度,提高二叉搜索树的性能
- AVL平衡因子为-1或0或1,为-2或2时表示不平衡,所以在一棵正确的AVL树中平衡因子的绝对值都小于等于1
- AVL树通过平衡因子调节树高度的方式是树旋转
例子
平衡因子为-1
平衡因子为0
平衡因子为1
AVL树的结点
三叉链结构,不仅有左右孩子,还有指向父亲的指针。
_bf表示平衡因子。
struct AVLTreeNode
{
AVLTreeNode* _left;
AVLTreeNode* _right;
AVLTreeNode* _parent;
pair_kv;
int _bf;//平衡因子
AVLTreeNode(const pair& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
};
AVL树的插入
插入过程
代码
找位置插入是二叉搜索树的知识,处理平衡因子是重点
- 更新平衡因子,新增结点插入在父节点的左边,父节点平衡因子–
- 更新平衡因子,新增结点插入在父节点的右边,父节点平衡因子++
- 二叉搜索树插入相关知识传送门
- 更新平衡因子的过程中,若更新后的平衡因子变为-1或1,表示需要继续向上更新,若为0,无需更新,也无需旋转,若为-2或2,表示此时这棵树需要旋转
平衡因子变为-1或1,说明是从0状态过来的(合格的avl树不会有-2和2,因为出现2和-1就被处理了),说明树的高度变化,需要继续更新。
平衡因子变为0,说明是从-1或1状态过来的,此时没有改变树的高度,所以无需处理,也不用向上更新
平衡因子变为2或-2,不符合avl树定义,进行旋转操作使平衡因子减小.
bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* cur_parent = nullptr;
while (cur)
{
if (kv.first < (cur->_kv).first)
{
cur_parent = cur;
cur = cur->_left;
}
else if (kv.first > (cur->_kv).first)
{
cur_parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(kv);
if (kv.first < (cur_parent->_kv).first)
{
//插在左边
cur_parent->_left = cur;
cur->_parent = cur_parent;//三叉链还得注意父亲
}
else
{
//擦在右间
cur_parent->_right =cur;
cur->_parent = cur_parent;
}
//处理平衡因子
while (cur_parent)
{
if (cur_parent->_left==cur)
{
(cur_parent->_bf)--;
}
else
{
(cur_parent->_bf)++;
}
if (cur_parent->_bf == 0)
{
break;
}
else if (cur_parent->_bf == 1 || cur_parent->_bf == -1)
{
//继续往上调整
cur = cur_parent;
cur_parent = cur->_parent;
}
else if (cur_parent->_bf == 2 || cur_parent->_bf == -2)
{
//为+-2就是不平衡
if (cur_parent->_bf == -2 && cur->_bf == -1)
{
//右旋
RotateR(cur_parent);
}
else if (cur_parent->_bf == 2 && cur->_bf == 1)
{
//左旋
RotateL(cur_parent);
}
else if (cur_parent->_bf == -2 && cur->_bf == 1)
{
//左右双旋
RotateLR(cur_parent);
}
else if (cur_parent->_bf == 2 && cur->_bf == -1)
{
//右左双旋
RotateRL(cur_parent);
}
else
{
assert(false);
}
break;
}
}
return true;
}
例子
注意:下面动图的平衡因子全都是反的,和网站有关,网站的平衡因子是把左子树高度减去右子树高度,所以观看动图时只需注意更新路径和旋转过程
直线or折线
若树需要进行旋转处理,且平衡因子更新轨迹是直线,则单旋(旋转一次)
若树需要进行旋转处理,且平衡因子更新轨迹是折线,则双旋(旋转两次)
所以下面我们先了解平衡因子的更新轨迹
更新平衡因子的轨迹是直线
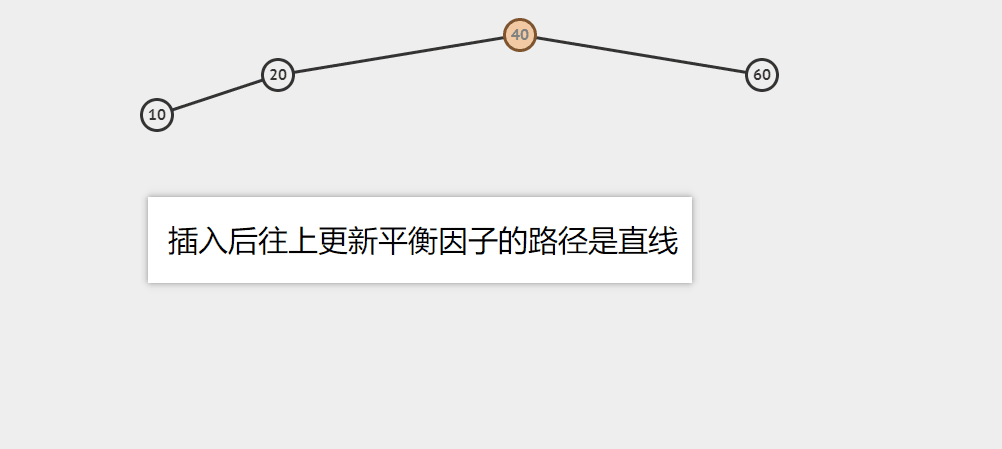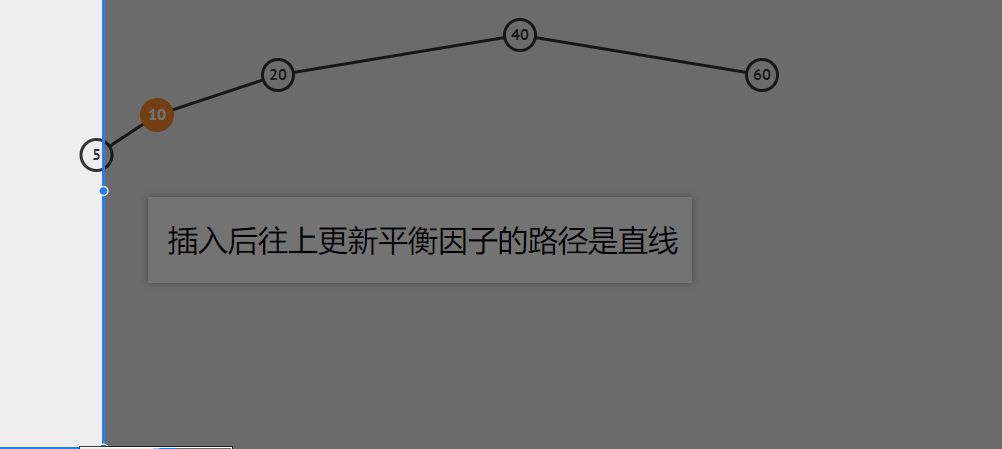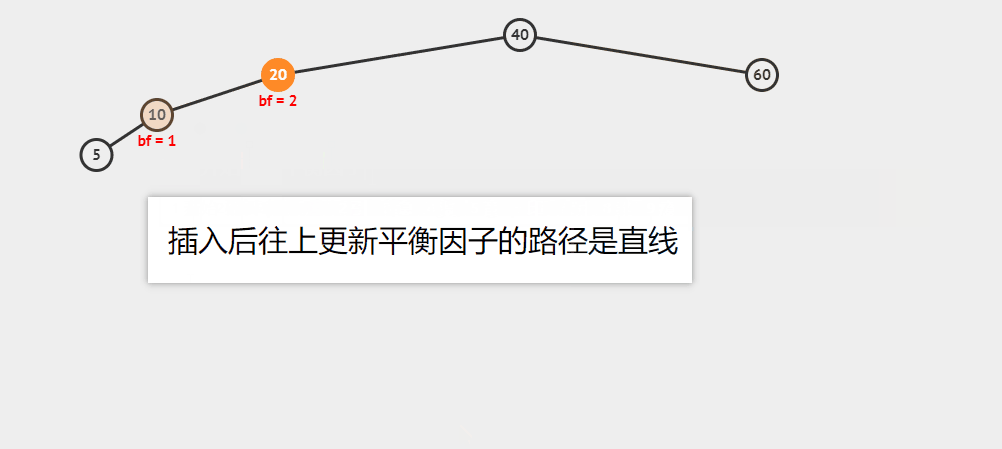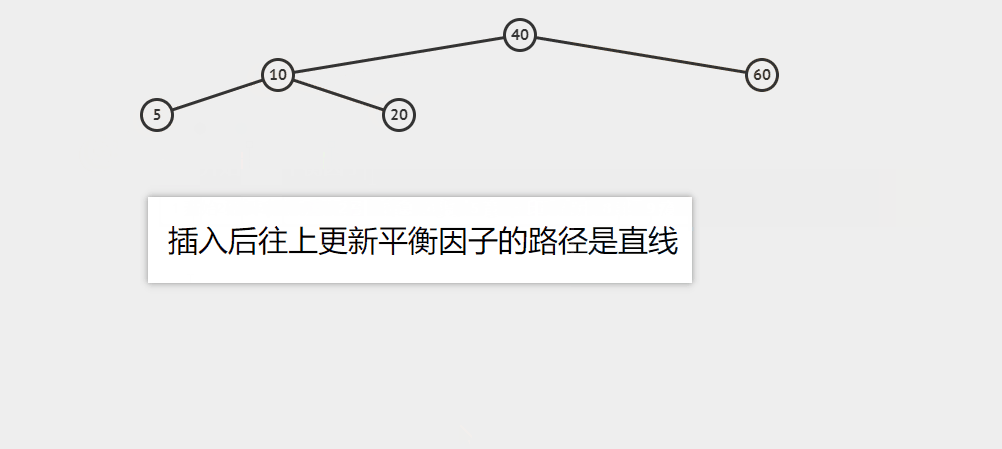
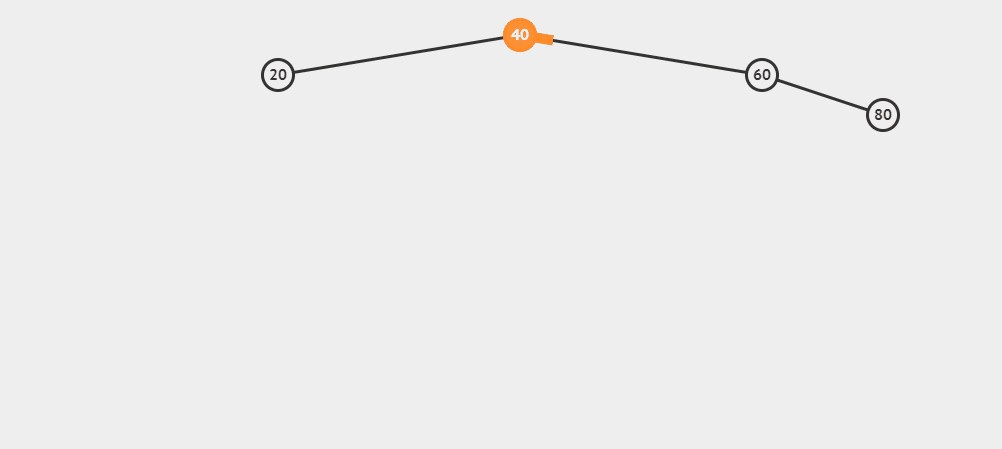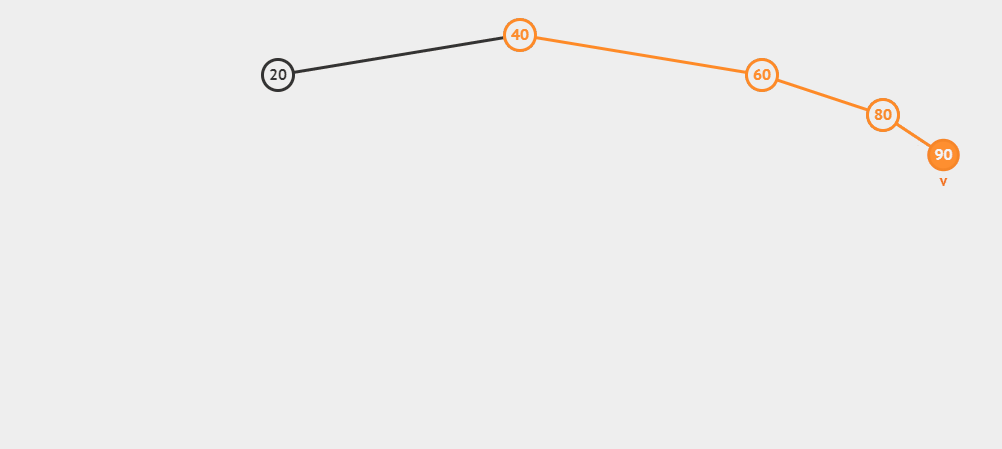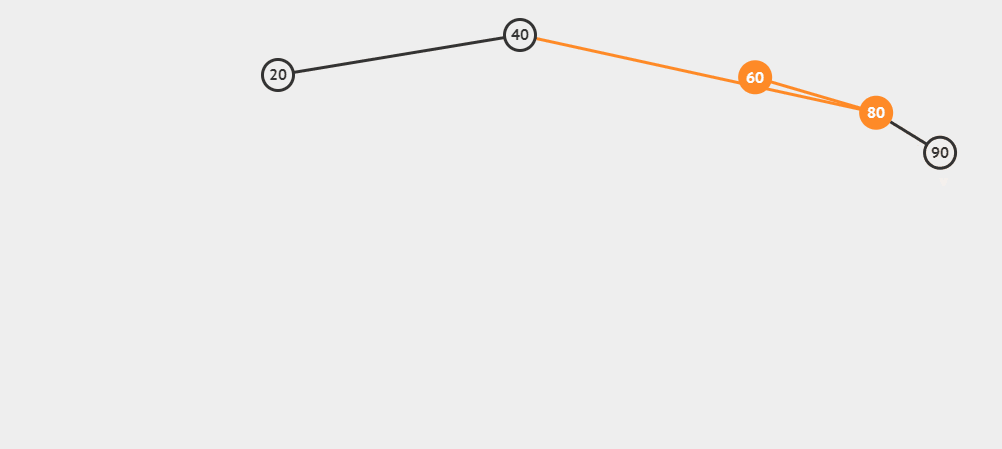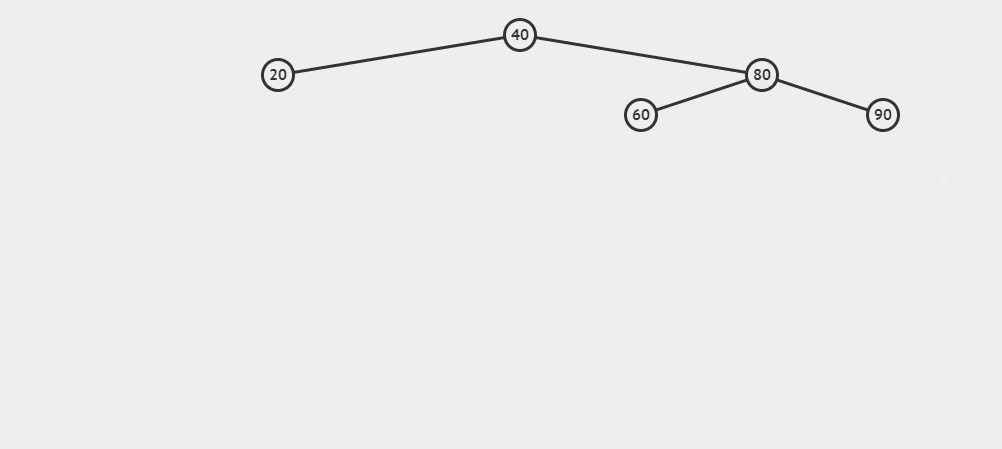
插入5为例
这里结点10的bf为-1,20的bf(平衡因子)为-2
更新平衡因子的轨迹是折线
插入15为例
树的旋转
左单旋
左旋的意思是以一个结点为中心往左边转
应用场景:直线(平衡因子的更新轨迹),结点的平衡因子为2
翻译:平衡因子的更新轨迹为直线,且有一个结点的右子树比左子树更高,高2。
理解:左旋是往左边转,就是把左边的子树”往下拉“,即让左子树深度变深使得整棵树平衡。
文字过程:
把平衡因子为2的结点记为parent,其右孩子记为subR,右孩子的左孩子记为subRL,parent往下移,subR往上移,此时subRL无人接管,交给parent接管,再更新平衡因子。这个图要自己画不然很难理解
抽象图
例子
代码实现
- subRL可能为空
- 旋转的中心可能上面还有父亲,即旋转的这棵树可能只是子树
- 旋转中心为根时
- 更新平衡因子
- 更新了指向孩子的指针后别忘了更改指向父亲的指针(三叉链结构)
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
subR->_bf = parent->_bf = 0;
}
右单旋
右旋的意思是以一个结点为中心往右边转
应用场景:直线(平衡因子的更新轨迹),结点的平衡因子为-2
翻译:平衡因子的更新轨迹为直线,且有一个结点的左子树比右子树更高,高2。
理解:右旋是往右边转,就是把右边的子树”往下拉“,即让右子树深度变深使得整棵树平衡。
文字过程:
把平衡因子为2的结点记为parent,其左孩子记为subL,左孩子的右孩子记为subLR,parent往下移,subL往上移,此时subLR无人接管,交给parent接管,再更新平衡因子。这个图要自己画不然很难理解
抽象图
例子
代码实现
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
//subLR可能为空
//subL可能为根节点
//subL上面还有结点
//更新平衡因子
//别忘了更新指向父亲的指针
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
//十分重要的一点 别忘了更新父亲
subL->_parent = ppNode;
}
subL->_bf = parent->_bf = 0;
}
左右双旋
先左单旋再右单旋
场景:平衡因子更新轨迹为折线,出现平衡因子为-2的结点
原理:轨迹为折线时,一次单旋无法得到正确的结果。需要先单旋把折线转为直线,再进行一次单旋调节高度.
抽象图
代码实现
void RotateLR(Node* parent)
{
//针对左子树的折线
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf; //记录下平衡因子,旋转后平衡因子发生了变化
RotateL(parent->_left);
RotateR(parent);
if (bf == -1)
{
parent->_bf = 1;
subLR->_bf = subL->_bf = 0;
}
else if (bf == 1)
{
subL->_bf = -1;
subLR->_bf = parent->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subL->_bf = subLR->_bf = 0;
}
else
{
assert(false);
}
}
右左双旋
先右单旋再左单旋
场景:平衡因子更新轨迹为折线,出现平衡因子为-2的结点
原理:轨迹为折线时,一次单旋无法得到正确的结果。需要先单旋把折线转为直线,再进行一次单旋调节高度
抽象图
代码实现
- 插入的结点在父节点的左边还是右边平衡因子的变化不同,故难点在于平衡因子的更新,具体的更新可以自己画图理解
void RotateRL(Node* parent)
{
//针对右子树的折线
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == -1)
{
subR->_bf = 1;
parent->_bf = subRL->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = -1;
subR->_bf = subRL->_bf = 0;
}
else if (bf == 0)//有三个节点时的特殊情况
{
subR->_bf = 0;
subRL->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}
其实看完两个抽象图可以知道,双旋就是把两个高度为h-1的子树给了parent和子树的父节点的父节点
检验是否是AVL树
检验标准
- 左右子树的高度差的绝对值是不是小于2?
- 右子树高度-左子树高度会不会等于根节点的平衡因子?
- 左右子树是不是avl树?
三个条件都满足时才是合格的avl树
代码实现
int _Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
int LHeight = _Height(root->_left) ;
int RHeight = _Height(root->_right) ;
return ((LHeight > RHeight) ? LHeight+1 : RHeight+1) ;
}
bool IsBalance()
{
return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int LHeight = Height(root->_left);
int RHeight = Height(root->_right);
if (root->_bf != (RHeight - LHeight))
{
cout << "平衡因子失常" << endl;
return false;
}
return abs(LHeight - RHeight) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
总结
-
AVL树在二叉搜索树的基础上增加了平衡因子来控制树的高度,进而提高了查找效率,查找的时间复杂度(logn)
-
如果对AVL树进行删除修改等操作,可能旋转多次,效率较低,所以AVL树常用于静态的数据(即不会改变),若是存储经常修改的效率,AVL树的效率并不高
-
红黑树在二叉搜索树的基础上增加了红黑两个颜色,也可以控制树的高度,此外红黑树的效率比AVL树更高,因为红黑树在构建时不需要像AVL树一样旋转那么多次(需要旋转 但不用旋转那么多次)
(AVL树代码汇总–github链接)