【数据结构】红黑树 的介绍及模拟实现
文章目录
- 1. 红黑树的概念
- 2. 红黑树的性质
- 3. 红黑树的结构
- 4. 红黑树节点的定义
- 5. 红黑树的迭代器
- 6. 红黑树节点的插入
- 7. 红黑树的验证
- 8. 红黑树的应用
-
- 7.1 Linux内核中红黑树的定义解析
- 9. 红黑树模拟实现完整代码
1. 红黑树的概念
红黑树(英语:Red–black tree)是一种自平衡二叉搜索树,是在计算机科学中用到的一种数据结构,典型用途是实现关联数组。它在1972年由鲁道夫·贝尔发明,被称为"对称二叉B树",它现代的名字源于Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文。红黑树的结构复杂,但它的操作有着良好的最坏情况运行时间,并且在实践中高效:它可以在O(log n)时间内完成查找、插入和删除,这里的n是树中元素的数目。
- 在计算机科学中,关联数组(英语:Associative Array),又称映射(Map)、字典(Dictionary)是一个抽象的数据结构,它包含着类似于(键,值)的有序对。一个关联数组中的有序对可以重复(如C++中的multimap)也可以不重复(如C++中的map)。
2. 红黑树的性质
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色,对于任何有效的红黑树,需要满足以下性质:
- 每个结点不是红色就是黑色
- 根节点必须是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
红黑树图例
关键特性:通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍
3. 红黑树的结构
head头结点中:
- parent指针指向null
- left指针指向树中最小值结点
- right指针指向树中最大值结点
root根结点的parent指针指向head头结点
4. 红黑树节点的定义
节点样式
// 红黑树节点的颜色
enum Color
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* left; // 节点的左孩子
RBTreeNode<T>* right; // 节点的右孩子
RBTreeNode<T>* parent; // 节点的父节点
T data; // 节点中保存的值
Color color; // 节点的颜色
// 将结点颜色默认设置为红色,因为如果设置成黑色会破坏原有黑色节点的个数
RBTreeNode(const T& x = T(), Color c = RED) :left(nullptr), right(nullptr), parent(nullptr), data(x), color(c){}
};
// 红黑树结构及定义
// T : 表示红黑树中放置的元素类型
// KOFP:表示从T中提取Key
template<class T, class KOFP>
class RBTree
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T> iterator; //迭代器
private:
Node* head; // 指向红黑树头结点的指针
size_t _size; // 保存红黑树的节点个数
};
5. 红黑树的迭代器
红黑树的迭代器实现了:重载了++、–、!=、==、*、->这些操作符
// 迭代器
template<class T>
struct RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T> self;
public:
RBTreeIterator(Node* n = nullptr) : node(n){}
// 具有指针类似的方法
T& operator*()
{
return node->data;
}
T* operator->()
{
return &(operator*());
}
/*
找比当前节点大的 所有节点中最小的节点:
1. 如果当前节点的右子树存在,应该在其右子树中找最小值节点(最左侧)
2. 如果当前节点的右子树不存在,应该在其双亲中不断查找
*/
self& operator++()
{
Increment();
return *this;
}
self& operator++(int)
{
self temp(*this);
Increment();
return temp;
}
/*
找比当前迭代器小的 所有节点中最大的:
1. 如果当前节点的左子树存在,应该在其左子树中找最大值节点(最右侧)
2. 如果当前节点的左子树不存在,
*/
self& operator--()
{
Decrement();
return *this;
}
self& operator--(int)
{
self temp(*this);
Decrement();
return temp;
}
bool operator!=(const self& s)const
{
return node != s.node;
}
bool operator==(const self& s)const
{
return node == s.node;
}
private:
Node* node; // 封装 节点指针
// 找当前迭代器的后一个位置
void Increment()
{
if (node->right)
{
// 当前节点的右子树如果存在,就在右子树中寻找最小值
node = node->right;
while (node->left)
{
node = node->left;
}
}
else
{
// 当前节点的右子树不存在,在父节点中寻找比当前节点大的节点
// 什么情况下才算大呢? 当node是双亲的左孩子时,才算找到
Node* parent = node->parent;
while (node == parent->right)
{
node = parent;
parent = parent->parent;
}
// 防止特殊情况:当根结点没有右子树时,迭代器恰好在根节点的位置
if (node->right != parent)
node = parent; // 此时node才指向父节点中比之前节点大的节点
}
}
// 找当前迭代器的前一个位置
void Decrement()
{
if (node == node->parent->parent && RED == node->color)
{
// node 在 end 的位置
node = node->right;
}
else if (node->left)
{
// 到 node 的左子树找最大的节点
node = node->left;
while (node->right)
{
node = node->right;
}
}
else
{
// 右子树不存在 -> 应该到 node 的双亲中找出比 node 小的节点
Node* parent = node->parent;
while (node == parent->left)
{
node = parent;
parent = node->parent;
}
node = parent;
}
}
};
6. 红黑树节点的插入
插入会遇到的破坏性质的三种情况:
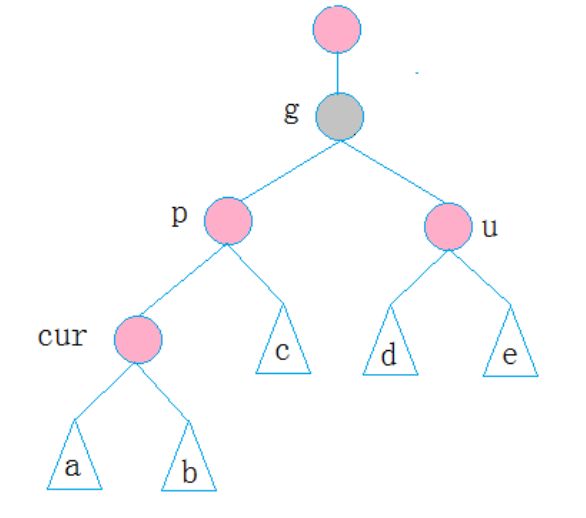
情况1:当前插入的节点是红色的,父节点是红色的,祖父节点是黑色的,叔叔节点存在且为红色
解决方法:将父节点和叔叔节点变为黑色,将祖父节点变为红色,
情况二:cur为红,p为红,g为黑,u不存在/u为黑
解决方式:
①p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,p为g的右孩子,cur为p的右孩子,则进行左单旋转
②p、g变色–p变黑,g变红
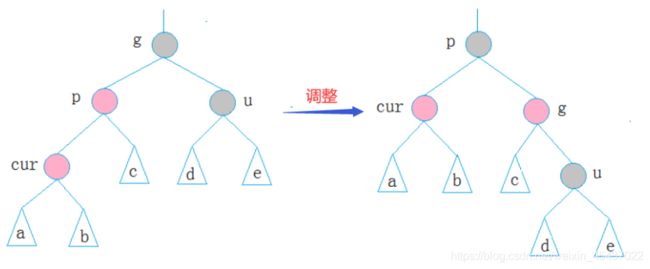
情况三:cur为红,p为红,g为黑,u不存在/u为黑
解决方式:
①p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转,则转换成了情况2
②按照情况二进行处理
代码实现
// 插入数据构造红黑树
pair<iterator, bool> insert(const T& data)
{
Node*& root = getRoot(); // 保存根结点
// 1. 按照BST的规则寻找插入结点的位置
// 1.1 若root为空,则需要建立root节点
if (nullptr == root)
{
root = new Node(data, BLACK); // 根结点默认为黑色
root->parent = head;
head->left = root;
head->right = root;
_size = 1;
return make_pair(iterator(root), true);
}
// 1.2 若root不为空,则需要寻找插入位置
Node* cur = root;
Node* parent = head;
KOFP key;
while (cur)
{
parent = cur;
if (key(data) < key(cur->data))
cur = cur->left;
else if (key(data) > key(cur->data))
cur = cur->right;
else // 该节点存在
return make_pair(iterator(cur), true);
}
// 1.3 找到插入位置后,插入新节点
Node* newNode = new Node(data);
cur = newNode;
if (data < parent->data)
parent->left = cur;
else
parent->right = cur;
cur->parent = parent;
// 2. 检测是否违反性质:检测新入节点预期双亲节点的颜色是否都为红色
while (parent != head && RED == parent->color)
/*
向上迭代的终止条件:
1. 若双亲节点颜色为黑色则表示不需要调整,反之需要调整
2. parent节点到达head时继续调整,反之停止调整
*/
{
// 违反性质表现:cur和parent两个节点都是红色的
Node* grandFather = parent->parent;
if (parent == grandFather->left)
{
// 情况一二三:双亲在祖父节点的左侧
Node* uncle = grandFather->right;
if (uncle && RED == uncle->color)
{
/*
情况一:uncle结点存在且为红色
解决方法:
1. cur父节点颜色变为黑色
2. cur祖父节点颜色变为红色
3. 向上迭代cur和parent指针
*/
parent->color = BLACK;
uncle->color = BLACK;
grandFather->color = RED;
cur = grandFather;
parent = cur->parent;
}
else //情况2和情况3
{
// uncle节点不存在 || uncle节点为黑色
if (cur == parent->right)
{
// 情况3 : 转化为 情况2
LeftRotation(parent);
std::swap(parent, cur);
}
// 情况2
grandFather->color = RED;
parent->color = BLACK;
RightRotation(grandFather);
}
}
else
{
// 情况一二三的镜像情况:双亲在祖父节点的右侧
Node* uncle = grandFather->left;
if (uncle && RED == uncle->color)
{
// 情况一:叔叔结点存在且为红色
parent->color = BLACK;
uncle->color = BLACK;
grandFather->color = RED;
cur = grandFather;
parent = cur->parent;
}
else
{
// uncle节点不存在 || uncle节点为黑色
if (cur == parent->left)
{
// 情况3 : 转化为 情况2
RightRotation(parent);
std::swap(parent, cur);
}
// 情况2
parent->color = BLACK; // while循环终止条件达成
grandFather->color = RED;
LeftRotation(grandFather);
}
}
}
// 新节点插入后 更新头结点的左右指针
root->color = BLACK;
head->left = getLeftMin();
head->right = getRightMax();
_size++;
return make_pair(iterator(newNode), true);
}
7. 红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
演示代码
bool isValidRBTree()
{
// 空树是红黑树
Node* root = getRoot();
if (root == nullptr)
return true;
// 树非空 -> 使用性质确定
/*
性质:
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
*/
if (root->color != BLACK)
{
cout << "违反了性质2:根结点不是黑色的!" << endl;
return false;
}
// 性质3和性质4同时检测
size_t blackCount = 0;
Node* cur = root;
while (cur)
{
if (cur->color == BLACK)
blackCount++;
cur = cur->left;
}
size_t pathBlackCount = 0; // 用来保存单条路径中黑色节点的个数
return _ValidRBTree(root, pathBlackCount, blackCount);
}
bool _ValidRBTree(Node* root, size_t pathBlackCount, const size_t blackCount)
{
if (nullptr == root)
return true;
if (root->color == BLACK)
pathBlackCount++;
Node* parent = root->parent;
// parent != head 表示root一定不是红黑树的根结点,parent一定是有效节点
if (parent != head && parent->color == RED && root->color == RED)
{
cout << "违反性质3:存在连在一起的红色结点" << endl;
return false;
}
// root是一个叶子节点
if (root->left == nullptr && root->right == nullptr)
{
if (pathBlackCount != blackCount)
{
cout << "违反性质4:路径中黑色节点的个数不同!" << endl;
return false;
}
}
return _ValidRBTree(root->left, pathBlackCount, blackCount) && _ValidRBTree(root->right, pathBlackCount, blackCount);
}
8. 红黑树的应用
红黑色应用之处:
- C++STL库中的map和set底层结构
- Linux内核中使用了红黑树
7.1 Linux内核中红黑树的定义解析
Linux内核中定义的红黑树
struct rb_node
{
unsigned long rb_parent_color;
#define RB_RED 0
#define RB_BLACK 1
struct rb_node *rb_right;
struct rb_node *rb_left;
} __attribute__((aligned(sizeof(long))));
/* The alignment might seem pointless, but allegedly CRIS needs it */
struct rb_root
{
struct rb_node *rb_node;
};
粗略一看,这里似乎没有定义颜色的域,但这就是这里红黑树实现的一个巧妙的地方。rb_parent_color这个域其实同时包含了颜色信息以及父亲节点的指针,因为该域是一个long的类型,需要大小为sizeof(long)的对齐,那么在一般的32位机器上,其后两位的数值永远是0,于是可以拿其中的一位来表示颜色。事实上,这里就是使用了最低位来表示颜色信息。明白了这点,那么以下关于父亲指针和颜色信息的操作都比较容易理解了,其本质上都是对rb_parent_color的位进行操作。
#define rb_parent(r) ((struct rb_node *)((r)->rb_parent_color & ~3)) //低两位清0
#define rb_color(r) ((r)->rb_parent_color & 1)//取最后一位
#define rb_is_red(r) (!rb_color(r)) //最后一位为0?
#define rb_is_black(r) rb_color(r) //最后一位为1?
#define rb_set_red(r) do { (r)->rb_parent_color &= ~1; } while (0) //最后一位置0
#define rb_set_black(r) do { (r)->rb_parent_color |= 1; } while (0) //最后一位置1
static inline void rb_set_parent(struct rb_node *rb, struct rb_node *p)//设置父亲
{
rb->rb_parent_color = (rb->rb_parent_color & 3) | (unsigned long)p;
}
static inline void rb_set_color(struct rb_node *rb, int color) //设置颜色
{
rb->rb_parent_color = (rb->rb_parent_color & ~1) | color;
}
9. 红黑树模拟实现完整代码
// 红黑树颜色定义
enum Color
{
RED,
BLACK
};
// 红黑树结点定义
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* left; // 节点的左孩子
RBTreeNode<T>* right; // 节点的右孩子
RBTreeNode<T>* parent; // 节点的父节点
T data; // 节点中保存的值
Color color; // 节点的颜色
RBTreeNode(const T& x = T(), Color c = RED) :left(nullptr), right(nullptr), parent(nullptr), data(x), color(c){}
};
// 迭代器
template<class T>
struct RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T> self;
public:
RBTreeIterator(Node* n = nullptr) : node(n){}
// 具有指针类似的方法
T& operator*()
{
return node->data;
}
T* operator->()
{
return &(operator*());
}
/*
找比当前节点大的 所有节点中最小的节点:
1. 如果当前节点的右子树存在,应该在其右子树中找最小值节点(最左侧)
2. 如果当前节点的右子树不存在,应该在其双亲中不断查找
*/
self& operator++()
{
Increment();
return *this;
}
self& operator++(int)
{
self temp(*this);
Increment();
return temp;
}
/*
找比当前迭代器小的 所有节点中最大的:
1. 如果当前节点的左子树存在,应该在其左子树中找最大值节点(最右侧)
2. 如果当前节点的左子树不存在,
*/
self& operator--()
{
Decrement();
return *this;
}
self& operator--(int)
{
self temp(*this);
Decrement();
return temp;
}
bool operator!=(const self& s)const
{
return node != s.node;
}
bool operator==(const self& s)const
{
return node == s.node;
}
private:
Node* node; // 封装 节点指针
// 找当前迭代器的后一个位置
void Increment()
{
if (node->right)
{
// 当前节点的右子树如果存在,就在右子树中寻找最小值
node = node->right;
while (node->left)
{
node = node->left;
}
}
else
{
// 当前节点的右子树不存在,在父节点中寻找比当前节点大的节点
// 什么情况下才算大呢? 当node是双亲的左孩子时,才算找到
Node* parent = node->parent;
while (node == parent->right)
{
node = parent;
parent = parent->parent;
}
// 防止特殊情况:当根结点没有右子树时,迭代器恰好在根节点的位置
if (node->right != parent)
node = parent; // 此时node才指向父节点中比之前节点大的节点
}
}
// 找当前迭代器的前一个位置
void Decrement()
{
if (node == node->parent->parent && RED == node->color)
{
// node 在 end 的位置
node = node->right;
}
else if (node->left)
{
// 到 node 的左子树找最大的节点
node = node->left;
while (node->right)
{
node = node->right;
}
}
else
{
// 右子树不存在 -> 应该到 node 的双亲中找出比 node 小的节点
Node* parent = node->parent;
while (node == parent->left)
{
node = parent;
parent = node->parent;
}
node = parent;
}
}
};
// 红黑树结构及定义
// T : 表示红黑树中放置的元素类型
// KOFP:表示从T中提取Key
template<class T, class KOFP>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef RBTreeIterator<T> iterator;
RBTree()
{
_size = 0;
head = new Node();
head->left = head;
head->right = head;
head->parent = nullptr; // 由于RBT中无节点,故头结点的父指针指向nullptr
}
~RBTree()
{
Destroy(head->parent);
delete head;
head = nullptr;
_size = 0;
}
// 迭代器
iterator begin()
{
return iterator(head->left);
}
iterator end()
{
return iterator(head);
}
// 插入数据构造红黑树
pair<iterator, bool> insert(const T& data)
{
Node*& root = getRoot(); // 保存根结点
// 1. 按照BST的规则寻找插入结点的位置
// 1.1 若root为空,则需要建立root节点
if (nullptr == root)
{
root = new Node(data, BLACK); // 根结点默认为黑色
root->parent = head;
head->left = root;
head->right = root;
_size = 1;
return make_pair(iterator(root), true);
}
// 1.2 若root不为空,则需要寻找插入位置
Node* cur = root;
Node* parent = head;
KOFP key;
while (cur)
{
parent = cur;
if (key(data) < key(cur->data))
cur = cur->left;
else if (key(data) > key(cur->data))
cur = cur->right;
else // 该节点存在
return make_pair(iterator(cur), true);
}
// 1.3 找到插入位置后,插入新节点
Node* newNode = new Node(data);
cur = newNode;
if (data < parent->data)
parent->left = cur;
else
parent->right = cur;
cur->parent = parent;
// 2. 检测是否违反性质:检测新入节点预期双亲节点的颜色是否都为红色
while (parent != head && RED == parent->color)
/*
向上迭代的终止条件:
1. 若双亲节点颜色为黑色则表示不需要调整,反之需要调整
2. parent节点到达head时继续调整,反之停止调整
*/
{
// 违反性质表现:cur和parent两个节点都是红色的
Node* grandFather = parent->parent;
if (parent == grandFather->left)
{
// 情况一二三:双亲在祖父节点的左侧
Node* uncle = grandFather->right;
if (uncle && RED == uncle->color)
{
/*
情况一:uncle结点存在且为红色
解决方法:
1. cur父节点颜色变为黑色
2. cur祖父节点颜色变为红色
3. 向上迭代cur和parent指针
*/
parent->color = BLACK;
uncle->color = BLACK;
grandFather->color = RED;
cur = grandFather;
parent = cur->parent;
}
else //情况2和情况3
{
// uncle节点不存在 || uncle节点为黑色
if (cur == parent->right)
{
// 情况3 : 转化为 情况2
LeftRotation(parent);
std::swap(parent, cur);
}
// 情况2
grandFather->color = RED;
parent->color = BLACK;
RightRotation(grandFather);
}
}
else
{
// 情况一二三的镜像情况:双亲在祖父节点的右侧
Node* uncle = grandFather->left;
if (uncle && RED == uncle->color)
{
// 情况一:叔叔结点存在且为红色
parent->color = BLACK;
uncle->color = BLACK;
grandFather->color = RED;
cur = grandFather;
parent = cur->parent;
}
else
{
// uncle节点不存在 || uncle节点为黑色
if (cur == parent->left)
{
// 情况3 : 转化为 情况2
RightRotation(parent);
std::swap(parent, cur);
}
// 情况2
parent->color = BLACK; // while循环终止条件达成
grandFather->color = RED;
LeftRotation(grandFather);
}
}
}
// 新节点插入后 更新头结点的左右指针
root->color = BLACK;
head->left = getLeftMin();
head->right = getRightMax();
_size++;
return make_pair(iterator(newNode), true);
}
// 交换两棵树
void swap(RBTree<T, KOFP>& t)
{
std::swap(head, t.head);
std::swap(_size, t._size);
}
// 清空红黑树所有有效节点
void clear()
{
Destroy(getRoot());
_size = 0;
}
// 中序遍历红黑树
void inOrder()
{
InOrder(head->parent);
cout << endl;
}
// 判断该树是否为红黑树
bool isValidRBTree()
{
// 空树是红黑树
Node* root = getRoot();
if (root == nullptr)
return true;
// 树非空 -> 使用性质确定
/*
性质:
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
*/
if (root->color != BLACK)
{
cout << "违反了性质2:根结点不是黑色的!" << endl;
return false;
}
// 性质3和性质4同时检测
size_t blackCount = 0;
Node* cur = root;
while (cur)
{
if (cur->color == BLACK)
blackCount++;
cur = cur->left;
}
size_t pathBlackCount = 0; // 用来保存单条路径中黑色节点的个数
return _ValidRBTree(root, pathBlackCount, blackCount);
}
// 容量相关的操作
size_t size() const
{
return _size;
}
// 判断红黑树是否为空
bool empty()
{
return head->parent == nullptr;
}
// 查找某个节点并返回其引用
iterator find(const T& data)
{
Node* cur = getRoot();
KOFP key;
while (cur)
{
if (key(data) == key(cur->data))
return iterator(cur);
else if (key(data) < key(cur->data))
cur = cur->left;
else
cur = cur->right;
}
return end();
}
private:
Node* head; // 指向红黑树头结点的指针
size_t _size; // 保存红黑树的节点个数
bool _ValidRBTree(Node* root, size_t pathBlackCount, const size_t blackCount)
{
if (nullptr == root)
return true;
if (root->color == BLACK)
pathBlackCount++;
Node* parent = root->parent;
// parent != head 表示root一定不是红黑树的根结点,parent一定是有效节点
if (parent != head && parent->color == RED && root->color == RED)
{
cout << "违反性质3:存在连在一起的红色结点" << endl;
return false;
}
// root是一个叶子节点
if (root->left == nullptr && root->right == nullptr)
{
if (pathBlackCount != blackCount)
{
cout << "违反性质4:路径中黑色节点的个数不同!" << endl;
return false;
}
}
return _ValidRBTree(root->left, pathBlackCount, blackCount) && _ValidRBTree(root->right, pathBlackCount, blackCount);
}
void InOrder(Node* root)
{
if (root)
{
InOrder(root->left);
cout << root->data << " ";
InOrder(root->right);
}
}
void Destroy(Node* root)
{
if (root)
{
Destroy(root->left);
Destroy(root->right);
delete root;
root = nullptr;
}
}
void RightRotation(Node* parent)
{
Node* subL = parent->left; // 父节点的左孩子节点
Node* subLR = subL->right; // 父节点的左孩子节点的右孩子节点
/*
右单旋:
1. 父节点的左指针指向subLR,实现将parent的右子树下降一层
2. subL的右指针指向parent,实现将parent的左子树上升一层
*/
// 右单旋 1
parent->left = subLR;
if (subLR) // 避免左单支的场景:subLR是nullptr
subLR->parent = parent;
// 右单旋 2
subL->right = parent;
// 因为parent可能是某个节点的子树,因此在更新parent的双亲前必须先将其之前的双亲记录
Node* pparent = parent->parent; // 可能parent是非根结点,需要记录parent的父结点
parent->parent = subL;
subL->parent = pparent;
// parent可能是根节点:需要修改_root
// parent也可能是一棵子树: 需要修改pparent的左/右指针域的指向
if (head == pparent) // 若是根结点,修改树的root指向
{
// 旋转之前parent是根节点
head->parent = subL;
}
else // 若是非根结点,修改parent父节点的指针指向
{
// parent是某个节点的子树
if (parent == pparent->left) // 判断parent是父节点的哪个孩子节点
pparent->left = subL;
else
pparent->right = subL;
}
}
void LeftRotation(Node* parent)
{
Node* subR = parent->right; // 父节点的右孩子节点
Node* subRL = subR->left; // 父节点的右孩子节点的左孩子节点
/*
左单旋:
1. parent节点的右指针指向subRL,实现将parent的右子树下降一层
2. subR的左指针指向parent,实现将parent的左子树上升一层
*/
// 左单旋 1
parent->right = subRL;
if (subRL) // 避免:右单支, 防止subRL是nullptr
subRL->parent = parent;
// 左单旋 2
subR->left = parent;
Node* pparent = parent->parent; // 需要更新parent和subR的双亲
parent->parent = subR;
subR->parent = pparent;
// 旋转之前:parent可能是根结点,可能是非根结点
// parent是根节点:修改_root的指向
// parent是子树:修改原parent左||右指针域的指向
if (head == pparent) // 若是根结点,修改树的root指向
{
head->parent = subR;
}
else // 若是非根结点,修改parent父节点的指针指向
{
if (parent == pparent->left) // 判断parent是父节点的哪个孩子节点
pparent->left = subR;
else
pparent->right = subR;
}
}
Node*& getRoot() // 获取头结点
{
return head->parent;
}
Node*& getLeftMin()
{
Node* root = getRoot();
if (nullptr == root)
return head;
Node* cur = root;
while (cur->left)
cur = cur->left;
return cur;
}
Node*& getRightMax()
{
Node* root = getRoot();
if (root == nullptr) return head;
Node* cur = root;
while (cur->right)
cur = cur->right;
return cur;
}
};