机器学习之分类任务
常见的四种分类任务:二分类、多类别分类、多标签分类、不平衡分类
分类的定义:在机器学习中,分类是指针对输入数据中的给定示例预测其类别标签的预测性建模问题。
二分类:
二分类任务包含一个属于正常状态的类别和另一个属于异常状态的类别。通常使用预测每个样本的伯努利概率分布的模型来对二分类任务进行建模。
可用于二分类的常用算法包括:
-
逻辑回归;k最近邻算法;决策树;支持向量机;朴素贝叶斯;
有些算法是专为二分类而设计的,它们本身并不支持两个以上的类别,例如逻辑回归和支持向量机。
多类别分类:
多类别分类是指具有两个以上类别标签的分类任务。通常使用多元概率分布模型来对多类别分类任务进行建模。
可用于多类分类的流行算法包括:
-
k最近邻算法;决策树;朴素贝叶斯;随机森林;梯度提升;
用于解决二分类问题的算法可以适用于多分类问题。如逻辑回归和支持向量机。
多标签分类:
多标签分类是指具有两个或以上分类标签的分类任务,其中每个样本可以预测为一个或多个类别。通常使用预测多个输出的模型来对多标签分类任务进行建模,而每个输出都将作为伯努利概率分布进行预测。
用于二分类或多分类的分类算法不能直接用于多标签分类。可以使用标准分类算法的专用版本,即所谓的算法的多标签版本,包括:
-
多标签决策树;多标签随机森林;多标签梯度增强;
不平衡分类:
不平衡分类是指其中每个类别中的示例数不均匀分布的分类任务。通常,不平衡分类任务是二分类任务,其中训练数据集中的大多数样本属于正常类,而少数样本属于异常类。可以使用专门的方法例如对多数类进行欠采样或对少数类进行过采样来更改训练数据集中样本的组成。例如:
-
随机欠采样;SMOTE过采样;
在将模型拟合到训练数据集上时,可以使用专门的建模算法来采集少数类别的数据,例如成本敏感型机器学习算法。例如:
-
成本敏感的Logistic回归;成本敏感的决策树;成本敏感的支持向量机;
最后,由于分类报告的准确性可能会产生误导,因此可能需要其他性能指标。例如:
-
准确率;召回率;F值;
评价指标:
分类任务中的评价指标有准确率(Accuracy)、FPR、FNR、Recall、Precision、F-score、MAP、ROC曲线和AUC等,回归任务中的指标有(r)MSE、MAE、CC/PCC等。
总结:
1.将类别标签分配给输入示例的分类预测模型
2.二分类是指预测两个类别之一,而多分类则涉及预测两个以上类别之一。
3.多标签分类涉及为每个示例预测一个或多个类别,不平衡分类是指各个类别之间的示例分布不相等的分类任务。
区分「聚类」与「分类」
聚类和分类是两种不同的分析。
分类的目的是为了确定一个点的类别,具体有哪些类别是已知的,常用的算法是 KNN (k-nearest neighbors algorithm),是一种有监督学习。聚类的目的是将一系列点分成若干类,事先是没有类别的,常用的算法是 K-Means 算法,是一种无监督学习。
两者也有共同点,那就是它们都包含这样一个过程:对于想要分析的目标点,都会在数据集中寻找离它最近的点,即二者都用到了 NN (Nears Neighbor) 算法。
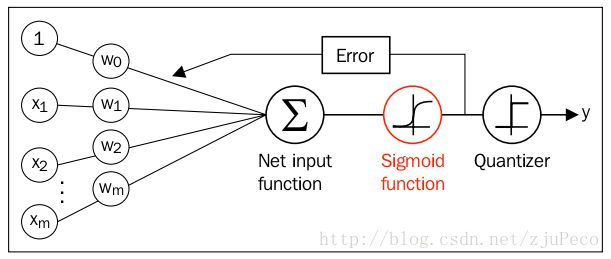
逻辑回归
该算法是根据现有数据对分类边界线建立回归公式,以此进行分类。希望分类器的输出值最好介于0到1之间,主要讨论的分类算法是逻辑回归,即logistic regression。逻辑回归一般用于二分类(Binary Classification)问题中,给定一些输入,输出结果是离散值。
Regression 常规步骤
-
寻找h函数(即预测函数)
-
构造J函数(损失函数)
-
想办法使得J函数最小并求得回归参数(θ)
构造预测函数h(x):
Logistic函数(或称为Sigmoid函数),函数形式为:
![]()
对于线性边界的情况,边界形式如下:
![]()
构造预测函数为:
![]()
函数h(x)的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为: P(y=1│x;θ)=hθ (x) P(y=0│x;θ)=1-hθ (x)
构造损失函数J(代价函数):
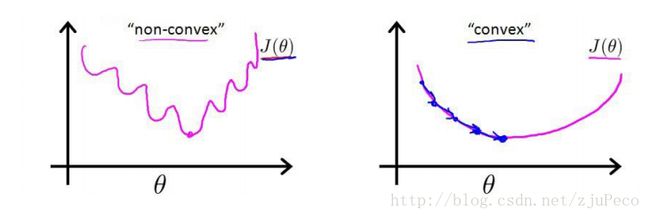
在线性回归中,代价项(Cost函数)会被定义为:1/2乘以预测值h和实际值观测的结果y的差的平方。这个代价值可以很好地用在线性回归里,但是对于逻辑回归却是不合适的。在逻辑回归中使用这个代价项(Cost函数)的问题在于非线性的sigmoid函数的出现导致J(θ)成为一个非凸函数。
找一个本身是凸函数的代价项(Cost函数),可以让我们使用类似于梯度下降的算法来找到一个全局最小值。换一个思路解决这个问题。
概率综合起来写成: ![]() 取似然函数为:
取似然函数为: ![]() 对数似然函数为:
对数似然函数为: ![]()
最大似然估计就是求使l(θ)取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。
将J(θ)取为下式,即: ![]()
函数形式如下:
![]()
从图中不难看出,如果样本的值是1的话,估计值ϕ(z)越接近1付出的代价就越小,反之越大;同理,如果样本的值是0的话,估计值ϕ(z)越接近0付出的代价就越小,反之越大。
此时θ是变量。我们的目标就是找出使J(θ)最小的θ值。
利用梯度下降法求参数:
sigmoid function有一个很好的性质就是ϕ′(z)=ϕ(z)(1−ϕ(z))![]()
θ更新过程可以写成: ![]()
优缺点:
优点:计算代价不高、容易理解和实现
缺点:容易欠拟合,分类精度不高